Метод А.Н.Крылова для решения системы линейных алгебраических уравнений

32.Метод А. Н. Крылова

В начале тридцатых годов нашего столетия А. Н. Крыловым был предложен достаточно удобный, метод нахождения собственных значений и собственных векторов матриц. Пусть D(λ) ≡det(λ E - A) = λⁿ + p₁ λ^n-1 + p₂ λ^n-2 + …., +  р_п  (5.1)

— характеристический полином (с точностью до знака) матрицы А. Согласно тождеству Гамильтона — Кели, матрица А обращает в нуль свой характеристический полином; поэтому Aⁿ  + p₁ A^n-1 +…+ p_n E = 0. (5.2) Возьмем теперь произвольный ненулевойвектор    y⁽⁰⁾ =Умножая обе части равенства (5.2) справа на  y⁽⁰⁾ получим:

Aⁿ  y⁽⁰⁾  + p₁ A^n-1 y⁽⁰⁾  +…+ p_n y⁽⁰⁾   = 0. (5.3)Положим: A^k  y⁽⁰⁾ = y^(k) (k=1, 2, ..., п); (5.4) тогда равенство (5.3) приобретает вид    y⁽ⁿ⁾ + p₁ y^(n-1) +…+ p_n y⁽⁰⁾  = 0. (5.5) или 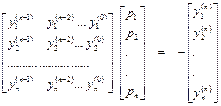  (5.5^*)гдеy^(k) =, (k=1, 2, ..., п).

Следовательно,   векторное   равенство   (5.5^*)  эквивалентно   системе уравнений  p₁ y_j ^(n-1) + p₂ y_j ^(n-2) + …., +  р_п y_j⁽⁰⁾ =  -y_j⁽ⁿ⁾(j = 1. 2. . . ., n),(5.6) из   которой  можно  определить неизвестные коэф­фициенты p₁, p_2,....., р_п . Так как на основании формулы (5.4)  y^(k) =A y^{(k -1)},    где (k= 1, 2, . . ., п),  то   координаты   y₁ ^(к) , y₂ ^(к) , …, y_n ^(к)   вектора    y^(k)последовательно вычисляются по формулам

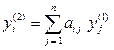  ,    ,…,   (5.7)     Таким образом, определение коэффициентов   p_jхарактеристи­ческого полинома (5.1) методом А. Н. Крылова сводится к решению линейной системы уравнений (5.6), коэффициенты которой вычи­сляются   по   формулам   (5.7),   причем   координаты   начального вектора

y⁽⁰⁾ =произвольны. Если система (6) имеет единственное решение, то ее корни р₁, р₂, ..., р_п являются коэффициентами характеристического полинома (5.1). Это решение может быть найдено, например, методом Гаусса. Если система (5.6) не имеет единственного решения, то задача усложняется . В этом случае рекомендуется изменить начальный вектор.