Метод отражений решения системы линейных алгебраических уравнений

19.Метод отражений

Этот метод основан на разложении матрицы  системы (4.1) в произведение унитарной матрицы на верхнюю треугольную. Матрица  называется унитарной, если она удовлетворяет уравнению , где  - матрица, сопряженная с . Вещественные унитарные матрицы называются ортогональными.

По своей структуре метод отражений близок к методу Гаусса, но исключение проводится с помощью матриц отражения, которые являются унитарными и эрмитовыми. Достоинством метода отражений является единая схема вычислительного процесса, не зависящая от структуры матрицы. Теорема 4.2. Пусть  и  произвольные вектор-столбцы, причем вектор  имеет единичную длину. Тогда найдется такой вектор , что построенная по нему матрица отражения  переведет вектор  в вектор, коллинеарный вектору , т.е. .Вектор  строится по правилу

,(4.16)где , .

Будем преобразовывать расширенную матрицу систему по правилу ,

с помощью умножения слева на последовательность матриц отражения . Для построения матрицы  на первом шаге метода в качестве вектора  берется первый столбец расширенной матрицы, а в качестве вектора  - координатный вектор . В силу выбора векторов  и  все координаты первого столбца расширенной матрицы, кроме первой, после выполнения первого шага метода будут равны нулю. Пусть уже построена матрица , у которой , , . Теперь в качестве  и  берутся вектора , ,где в векторе  единица стоит на -ом месте. После выполнения -го шага метода отражений получим матрицу , у которой все элементы, стоящие ниже главной диагонали, в первых -ом столбцах будут равны нулю. Невозможность выполнения очередного шага связана только с равенством нулю вектора , а это невозможно, так как матрица  является невырожденной. После - шага получим матрицу, первые  столбцов которой образуют верхнюю треугольную матрицу . Система уравнений, соответствующая полученной расширенной матрице, равносильна исходной системе (4.1). Значения неизвестных находятся аналогично обратному ходу метода Гаусса

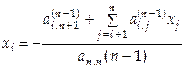, ,  Для решения системы линейных алгебраических уравнений методом отражений необходимо выполнить  операций умножения и деления, а также  извлечений квадратных корней.