где Bδ1 – расчетная эффективная индукция над сбегающим краем полюса с учетом опрокидывания поля.
С учетом уменьшения ширины полюсного деления поток под полюсом будет равен:
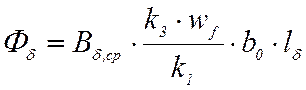 . (21)
. (21)
С учетом ранее принятых аппроксимаций для Bδ,ср имеем:
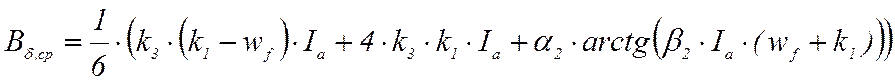 (22) при k1·Ia ≤ Ia,кр·wf
(22) при k1·Ia ≤ Ia,кр·wf
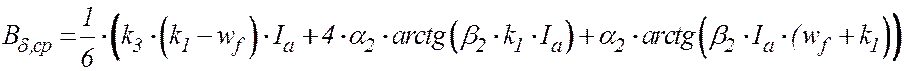 (23) при k1·Ia > Ia,кр·wf ;
(23) при k1·Ia > Ia,кр·wf ;
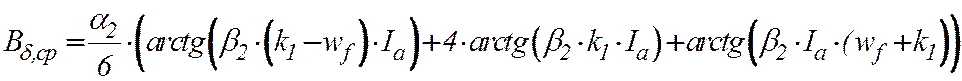 (24)
(24)
при (k1 – wf)·Ia > Ia,кр·wf .
В программе расчета на ЭВМ перед вычислением потока в воздушном зазоре Φδ ведется анализ ситуации в зависимости от величины тока якоря, и определяется соответствующая расчетная формула для определения Φδ.
Для переходного режима можно записать дифференциальное
уравнение для якорной цепи, подставив в (1) вместо jω оператор
дифференцирования ![]() . Учитывая, что (Xσa + Xσf)=(lσa+lσf)·ω1;
. Учитывая, что (Xσa + Xσf)=(lσa+lσf)·ω1;
(Xaq+ Xad ·sin αщ) = (Laq+ Lad ·sin αщ)·ω1, где lσa и lσf – соответственно индуктивности рассеяния обмоток якоря и возбуждения; Lad и Laq – индуктивности якоря по продольной и поперечной осям, получим:
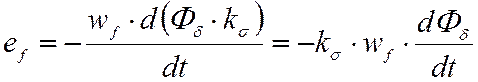 .
(25)
.
(25)
Уравнения для мгновенных значений с учетом насыщения можно записать в виде:
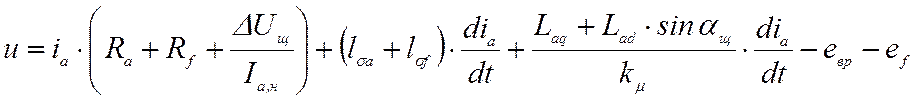 (26)
(26)
После преобразования (26) приводится к виду:
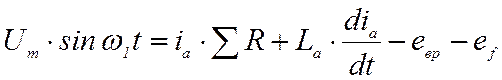 ,
(27)
,
(27)
где Um – амплитуда напряжения сети, В;
ω1 – угловая частота сетевого напряжения, с-1;
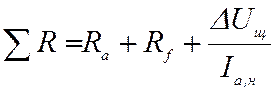 – активное сопротивление якорной
цепи, Ом;
– активное сопротивление якорной
цепи, Ом;
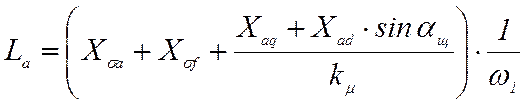 – общая индуктивность цепи якоря, Гн.
– общая индуктивность цепи якоря, Гн.
Мгновенное значение тока якоря, полученное в результате решения этого дифференциального уравнения, можно представить в виде:
ia=Iam·sin(ω1t+φ),
где Iam – амплитуда тока якоря, А; φ – фазовый сдвиг тока относительно напряжения, рад.
Во всех точках расчета потока под нагрузкой используется действующее значение тока якоря, определяемого из соотношения:
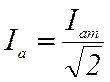 .
.
В соответствии с этим во всех точках расчета
мгновенное значение тока якоря делится на ![]() .
.
Поток Φδ, рассчитанный по приведенной методике, будет совпадать по фазе с током якоря.
2.3 Учет угла магнитного запаздывания
На рисунке 2 приведена векторная диаграмма для установившегося режима КД, построенная по уравнению (1) с учетом (6).
Как видно из векторной диаграммы, поток Φδ отстает от тока на угол γ, который обусловлен суммарными потерями в стали в номинальном режиме Pсн и электрическими потерями в коммутируемых секциях Pμt от трансформаторной ЭДС Еt, наводимой в коммутируемой секции.
Величина угла сдвига определяется из соотношения:
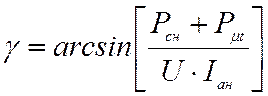 ,
(28)
,
(28)
где Pсн – магнитные потери в стали статора и якоря, Вт;
Pμt – потери в коммутируемой секции, Вт,
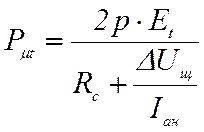 ,
(29)
,
(29)
Еt – трансформаторная ЭДС в коммутируемой секции, В;
Rc – активное сопротивление коммутируемой секции, Ом,
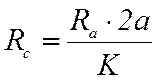 ,
,

Рисунок 2 – Векторная диаграмма коллекторного двигателя.
2a – число параллельных ветвей обмотки якоря, К – число коллекторных пластин.
В процессе расчета переходного процесса величина угла γ принята постоянной.
При определении мгновенных значений потока по уравнениям (17), (19) и (21) получаются мгновенные значения потока, изменяющегося в фазе с током якоря. Для получения реального значения магнитного потока, сдвинутого относительно мгновенного значения тока якоря на угол γ , необходимо выполнить вычисления согласно следующему уравнению:
![]()
![]() ,
(30)
,
(30)
где φδ – мгновенное значение действительного магнитного потока, Вб;
φδ1 и φδ2 – первая и вторая составляющие магнитного потока φδ, Вб.
Первая и вторая составляющие магнитного потока φδ сдвинуты во времени относительно друг друга на четверть периода. Вторая составляющая потока под нагрузкой φδ2 может быть рассчитана по разработанному алгоритму (по известному значению тока с учетом кривой намагничивания), если в расчете будет использоваться мгновенное значение тока, меняющегося по закону косинуса:
![]() .
(31)
.
(31)
Это значение может быть получено из решения дополнительного дифференциального уравнения якорной цепи:
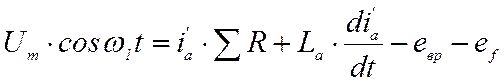 ,
(32)
,
(32)
отличающегося от (27) лишь фазой напряжения сети. Поскольку все параметры (32) совпадают с (27), то фазовый сдвиг тока относительно напряжения будет равен углу φ.
ЭДС трансформации определяется по закону электромагнитной индукции и может быть разложена с учетом потерь в стали на две составляющие (рисунок 2) в комплексной форме:
– совпадающую по направлению с током (она носит активный характер и складывается с падением напряжения на якоре)
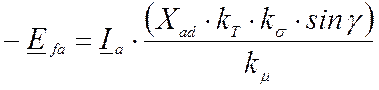 ,
(33)
,
(33)
где
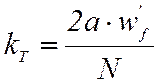 – коэффициент трансформации,
– коэффициент трансформации, ![]() – число витков обмотки возбуждения на
один полюс;
– число витков обмотки возбуждения на
один полюс;
– составляющую, имеющую индуктивный характер,
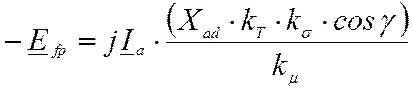 , (34)
, (34)
которая складывается с падением напряжения на индуктивности цепи якоря.
ЭДС вращения удобно разложить на две составляющие (рисунок 2) в комплексной форме:
– совпадающую по фазе с током якоря (активная составляющая, обусловленная потоком φδ1):
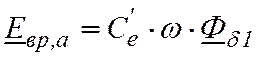 ,
(35)
,
(35)
– составляющую, сдвинутую по фазе на четверть периода (реактивная составляющая, обусловленная потоком φδ2):
![]() , (36)
, (36)
Таким образом, ЭДС вращения с учетом угла магнитного запаздывания представляется в виде:
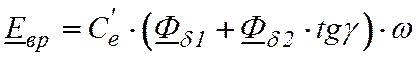 .
(37)
.
(37)
2.4 Уравнение моментов коллекторного двигателя
Электромагнитный момент КД определяется по уравнению, Н·м:
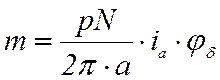 .
(38)
.
(38)
Проведя подстановку в (38) значений тока якоря ia и потока φδ в воздушном зазоре, получим:
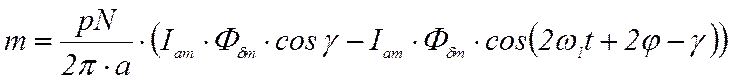 . (39)
. (39)
Это уравнение показывает, что момент имеет две составляющие:
– постоянную, соответствующую среднему моменту, Н·м,
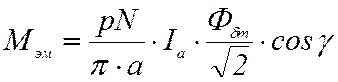 ,
(40)
,
(40)
Ia – действующее значение тока якоря, А;
– переменную составляющую, меняющуюся с двойной частотой, Н·м,
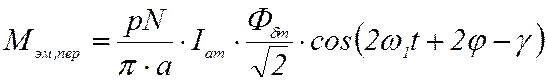 .
(41)
.
(41)
Электромагнитный момент уравновешивается моментом сопротивления нагрузки на валу Мс, динамическим моментом Мдин и моментом холостого хода М0.
Динамический момент на валу КД составляет, Н·м:
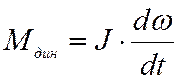 , (42)
, (42)
где J – момент инерции якоря и нагрузки, кг·м2.
Момент инерции якоря равен, кг·м2:
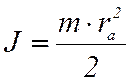 ,
(43)
,
(43)
где m – масса якоря, кг, ra – радиус якоря, м.
В единицах технической системы мер момент инерции определяется,
кг·м ·с2:
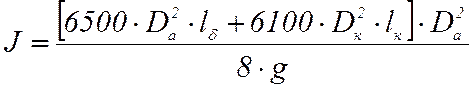 , (44)
, (44)
где Da – диаметр якоря ,м, Dк – диаметр коллектора, м, lк – длина коллектора, м, g – ускорение свободного падения, м/с2.
Момент холостого хода состоит из трех составляющих, Н·м:
– постоянной 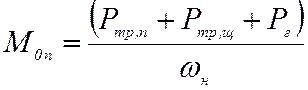 ;
;
– линейной 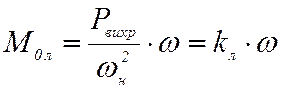 ;
;
– квадратичной 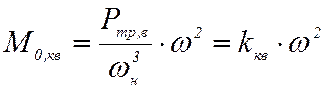 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.