Исследование переходных процессов в коллекторном двигателе переменного тока при пуске: Методические указания к лабораторной работе № 8, страница 2

В работе [6.5] приведены дифференциальные уравнения электромеханического преобразователя энергии переменного тока с коллектором и двумя парами щеток по продольной и поперечной осям. Из этой математической модели коллекторный двигатель переменного тока следует как частный случай. Но анализ показывает, что данная модель использует постоянные параметры, не учитывает магнитные потери, влияние насыщения и реакции якоря и носит приближенный характер. Хотя установившийся режим работы является частным и конечным случаем динамического режима, в соответствии с имеющейся литературой удобно начать рассмотрение физики явлений и учет разных факторов с установившегося режима, а затем перейти к дифференциальным уравнениям коллекторного двигателя.

2.1 Уравнение напряжений якорной цепи коллекторного двигателя

Коллекторный двигатель переменного тока (КД) имеет последовательное возбуждение. В установившемся режиме работы двигателя напряжение сети уравновешивается падением напряжения на активных и индуктивных сопротивлениях цепи якоря, а также тремя ЭДС – ЭДС вращения якоря, ЭДС, наводимой в обмотке якоря поперечным потоком, и трансформаторной ЭДС, наведенной в обмотке возбуждения магнитным потоком, проходящим через полюс:

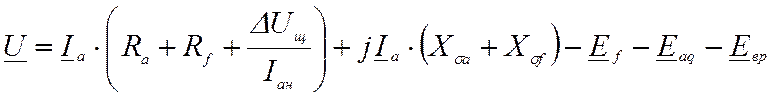,    (1)

где U– напряжение сети, В;

I_a  – ток якоря, А;

R_a  – активное сопротивление обмотки якоря, Ом;

R_f – активное сопротивление обмотки возбуждения, Ом;

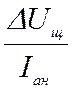– сопротивление щеточного контакта, Ом;

X_σa – индуктивное сопротивление якоря, обусловленное потоками рассеяния в пазах и вокруг лобовых частей обмотки якоря, Ом;

X_σf – индуктивное сопротивление обмотки возбуждения, обусловленное потоком рассеяния вокруг обмотки возбуждения, Ом;

  E_вр – ЭДС вращения, наводимая в обмотке якоря продольным потоком в воздушном зазоре при вращении якоря с угловой частотой ω, В,

E_вр=С'_е · ω ·Φ_δm,                                           (2)

     Φ_δm – поток в воздушном зазоре, Вб;

     С'_е – постоянная, зависящая от обмоточных данных;

E_f– трансформаторная ЭДС обмотки возбуждения, В, которая наводится потоком полюса Φ_fm; поток полюса складывается из потока в воздушном зазоре Φ_δm  и потока рассеяния Φ_σm, который замыкается между полюсами и не сцеплен с якорем и не участвует в наведении ЭДС вращения в обмотке якоря,

,          (3)

k_σ – коэффициент рассеяния полюсов, (обычно k_σ=1,1…1,2);

E_aq – ЭДС, наводимая в якоре поперечным потоком реакции якоря, В.

В отличие от машины постоянного тока, поток реакции якоря будет пульсировать с частотой сети и наводить в обмотке якоря ЭДС E_aq. При расчете E_aq  пренебрегают поперечным потоком в межполюсном пространстве. Возникающая при этом погрешность мала, так как длина магнитных силовых линий поперечного потока в пространстве между полюсами велика, а индукция незначительна [6.4].

Комплексная величина поперечной ЭДС определяется по формуле:

 E_aq = jX_aq· I_a,                                               (4)

где  X_aq – индуктивное сопротивление реакции якоря по поперечной оси, Ом.

Поток в воздушном зазоре обуславливает индуктивное сопротивление реакции якоря по продольной оси X_ad  и ЭДС:

E_ad = jX_ad· I_a,                                               (5)

где  X_ad – индуктивное сопротивление реакции якоря по продольной оси, Ом. Эта ЭДС не снимается с якоря, так как в КД отсутствуют щетки по продольной оси. Однако при сдвиге щеток с линии геометрической нейтрали против вращения на угол α_щ в поперечной цепи якоря появляется ЭДС [6.6]:

E'_ad = jX_ad· I_a·sin α_щ.                                              (6)

2.2 Учет влияния насыщения и реакции якоря

Учет насыщения магнитной цепи может быть проведен следующим образом.

Кривая зависимости потока при холостом ходе от МДС возбуждения может быть разбита на два участка:

– линейный участок на начальной части кривой, аппроксимированный формулой

  при I_a  ≤  I_a,кр,                                     (7)

где I_a,кр  – критическое значение тока якоря в точке отхода от линейной зависимости, А; w_f – число витков в обмотке возбуждения;

– нелинейный участок, аппроксимируемый зависимостью

 при I_a  >  I_a,кр,                          (8)

 где k₂, α₁ и β₁ – постоянные коэффициенты.

Тогда коэффициент насыщения можно рассчитать по формуле:

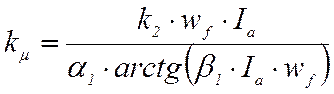.                                         (9)

При I_a  ≤  I_a,кр коэффициент насыщения равен единице.

Насыщенные значения параметров якоря будут равны:

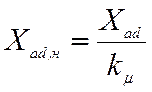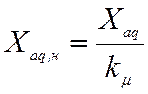,     .                                  (10)

Магнитный поток при нагрузке (поток в воздушном зазоре Φ_δm) уменьшается из-за размагничивающего действия поперечной реакции якоря при насыщении. Его значение под нагрузкой находится по переходной характеристике Φ_δm=f(F_δza), где F_δza – сумма МДС воздушного зазора, зубцов и ярма якоря.

Как и для потока, переходная характеристика для индукции в воздушном зазоре аппроксимируется на двух участках – линейном, с помощью уравнения

   при I_a  ≤  I_a,кр,                                     (11)

и нелинейном, аппроксимируемом функцией арктангенса

 при I_a  >  I_a,кр,                          (12)

где k₃, α₂ и β₂ – постоянные коэффициенты.

Тогда влияние реакции якоря или результирующий поток при нагрузке можно определить аналитическим методом Г.Н. Петрова [6.2]. (Рисунок 1).

Рисунок 1 – К определению размагничивающего действия реакции якоря при насыщении

МДС якоря под краем полюса, А:

 0,5b₀  A,

где b₀ – ширина полюсного наконечника, м; A –  линейная нагрузка, А/м,

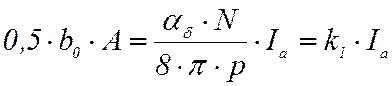,                                        (13)

α_δ – коэффициент полюсного перекрытия;

p – число пар полюсов;

N – число проводников якоря.

Величина потока в воздушном зазоре под нагрузкой определяется из соотношения

Φ_δ = Φ_m – ΔΦ,                                            (14)

где ΔΦ – изменение потока вследствие насыщения и размагничивающего действия реакции якоря.

Если нет опрокидывания поля и ток мал (I_a  ≤  I_a,кр, w_f – k₁ ≥ 0), то изменение потока составляет:

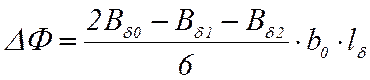,                                  (15)

где B_δ0 – индукция в зазоре под центром полюса, обусловленная током , протекающим в обмотке возбуждения, Тл;

B_δ1 – индукция в зазоре под сбегающим краем полюса, Тл;

B_δ2 – индукция в зазоре под набегающим краем полюса, Тл;

l_δ – длина воздушного зазора, м.

При принятых аппроксимациях (7), (8) и (11), (12) в случае I_a  ≤  I_a,кр,

w_f – k₁ ≥ 0 получим:

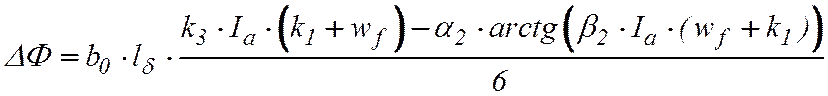 ,        (16)

.                                    (17)

Если I_a  >  I_a,кр, то

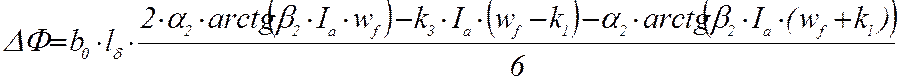, (18)

.                      (19)

Если имеет место опрокидывание поля, то есть w_f – k₁ < 0,  то может быть вычислена средняя индукция по формуле Симпсона, определяющая поток в воздушном зазоре при нагрузке:

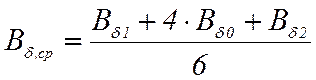 ,                                 (20)