Исследование переходных процессов в асинхронном двигателе c двухклеточным ротором: Методические указания к лабораторной работе № 7, страница 4

X12 – ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ ВЗАИМОИНДУКЦИИ X₁₂, Ом;

ROR – АКТИВНОЕ СОПРОТИВЛЕНИЕ ОБЩЕГО КОЛЬЦА R_O^', Ом;

RS – АКТИВНОЕ СОПРОТИВЛЕНИЕ СТАТОРА R₁, Ом.

В случае ошибки при вводе данных необходимо прервать работу программы нажатием клавиш Ctrl – Break и запустить программу заново.

После окончания ввода идет расчет с печатью графика тока. Далее ЭВМ дает запросы:

«Продолжить расчет? Да (1). Нет (2)» 2.

«Для расчета времени разбега введите установившееся значение скорости»                     <вводится значение номинальной частоты вращения>

«Будете выводить на печать график тока? Да (1). Нет (2)» 2.

«Будете выводить график момента? Да (1). Нет (2)» 2.

«Будете выводить на печать график скорости? Да (1). Нет (2)» 2.

На этом работа программы завершается. После этого формируется текстовый файл с именем «QKIMB3n. txt», причем n – номер опыта.

Для просмотра текстового файла необходимо выйти из среды QBASIC (пункт меню FILE – EXIT).  После чего, найдя нужный файл в Norton Commander (либо в Windows Commander, либо в DOS Navigator), отметить его курсором и открыть для просмотра клавишей F3. После проверки правильности ввода исходных данных текстовый файл с таблицей результатов следует распечатать.

Данные расчета выводятся в виде таблицы:

1 столбец – «Х» – текущее время с шагом h;

2 столбец – «IAS» – ток статора, А;

3 столбец – « ME» – электромагнитный момент, Н·м;

4 столбец – «N» –  частота вращения, мин^-1;

5 столбец – «S» – скольжение ротора в текущий момент времени.

4.2  К пункту 3.6

Время пуска определяется по осциллограмме частоты вращения n=f(t) (рисунок 5). Относительно установившегося значения откладываются две ординаты 0,95n_уст и 1,05n_уст. Процесс считается законченным, когда кривая частоты вращения последний раз пересечет горизонтальную   линию с ординатой 0,95n_уст  либо 1,05n_уст в соответствии с рисунком 5.

Рисунок 5 – Определение времени пуска АД по осциллограммам частоты вращения ротора: n_r1 – при значительных колебаниях частоты вращения;

n_r2 – при экспоненциальном нарастании частоты вращения;

n_r3 – при затухающих колебаниях частоты вращения.

4.3  К пункту 3.8

Электромеханическая постоянная времени Т_М характеризует быстродействие электродвигателя и характер изменения частоты вращения в переходных процессах. Эта постоянная времени равна:

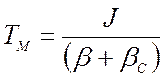,                                                (27)

где J– приведенный момент инерции на валу АД;

β – жесткость механической характеристики АД;

;

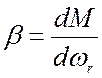β_С – жесткость механической характеристики нагрузочного механизма; в первом приближении можно считать, что момент нагрузки М_с не зависит от частоты вращения, то есть β_С =0 (абсолютно мягкая механическая характеристика нагрузочного механизма).

Жесткость механической характеристики АД приближенно можно определить как

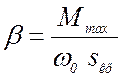,                                                    (28)

где М_max – максимальный момент АД; М_max = k_пM_ном,k_п – перегрузочная способность АД, о.е.;

ω₀ – синхронная частота вращения АД; ω₀=2πf₁ /p;

s_кр – критическое скольжение АД, о.е.

С учетом (27) и (28) электромеханическая постоянная времени АД равна:

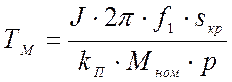.                                           (29)

Электрическая постоянная времени:

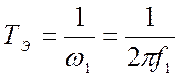.                                              (30)

При 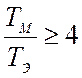 изменение частоты вращения носит экспоненциальный характер (график n_r2=f(t) на рисунке 5). При 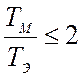 наблюдаются значительные колебания частоты вращения (график n_r1=f(t) на рисунке 5).

В отчете необходимо рассчитать Т_М по (29) и Т_Э по (30) и их отношение. Данные для расчета следует взять из таблицы 1 в соответствии с выданным вариантом.

5 Контрольные вопросы

5.1  В чем достоинства и недостатки системы дифференциальных уравнений АД, записанной в потокосцеплениях?

5.2  Объяснить физический смысл каждой составляющей суммарного момента, действующего на ротор асинхронного двигателя.

5.3  Как приводится сопротивление двойной беличьей клетки к эквивалентным сопротивлениям обычного двигателя, зависящим от скольжения?

5.4   Как организуется решение системы дифференциальных уравнений методом Рунге – Кутта?

5.5   Как определяется время пуска?

5.6 Что такое электромеханическая постоянная времени и как она влияет на характер переходного процесса?

6  Библиографический список

6.1  Копылов И.П. Математическое моделирование электрических машин. – М.: 2001.

6.2   Асинхронные двигатели серии 4А./ Справочник. Под ред. А.А. Кравчика и др. – М.: Энергоиздат, 1982.

6.3 Якимов В.В. Спецкурс электрических машин. – Горький, изд-во ГГУ,1989.

6.4   Сипайлов Г.А., Лоос А.В. Математическое моделирование электрических машин (АВМ). - М.: Высшая школа, 1980.

Таблица 1 – Исходные данные для расчета переходного процесса при пуске двухклеточного асинхронного двигателя при фазном напряжении 220 В и частоте сети f`₁ =50 Гц.