Пренебрежение величиной индуктивного сопротивления рассеяния верхней клетки Xв' , а также исключение взаимной индуктивности между верхней и нижнее клетками ротора в силу их относительной малости, практически не влияет на общий ток I'20 = Iв' + Iн' . Токи же I2в' и I2н' при указанном допущении мало отличаются от реальных приведенных токов в клетках – обычно не более, сем на 5-6 %.
При допущении Xв'=0 определяются активное ![]() и
индуктивное Xэ' сопротивления эквивалентной цепи, заменяющие собой
две параллельные ветви преобразованной схемы замещения. Полное сопротивление
этих параллельных ветвей:
и
индуктивное Xэ' сопротивления эквивалентной цепи, заменяющие собой
две параллельные ветви преобразованной схемы замещения. Полное сопротивление
этих параллельных ветвей:
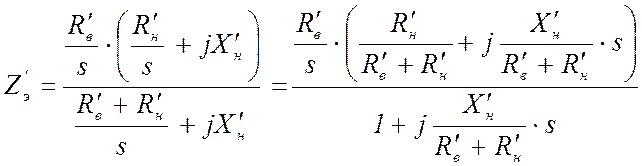 .
(13)
.
(13)
Если ввести обозначение
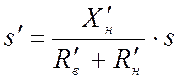 ,
(14)
,
(14)
то получается следующее выражение:
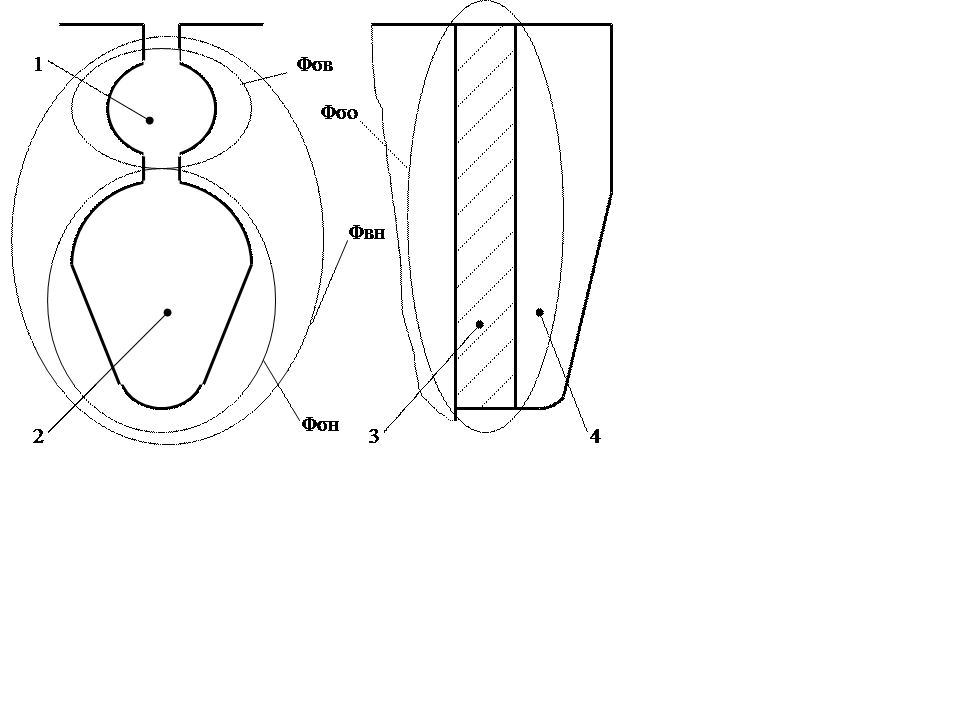
Рисунок 2 – Эскиз паза ротора двухклеточного асинхронного двигателя.
1 – стержень верхней клетки; 2 – стержень нижней клетки; 3 – короткозамыкающее кольцо; 4 – вентиляционная лопатка; Φσв – поток рассеяния верхней клетки; Φσн – поток рассеяния нижней клетки; Φвн – поток взаимной индукции между верхней и нижней клетками; Φσо – поток рассеяния короткозамыкающего кольца.
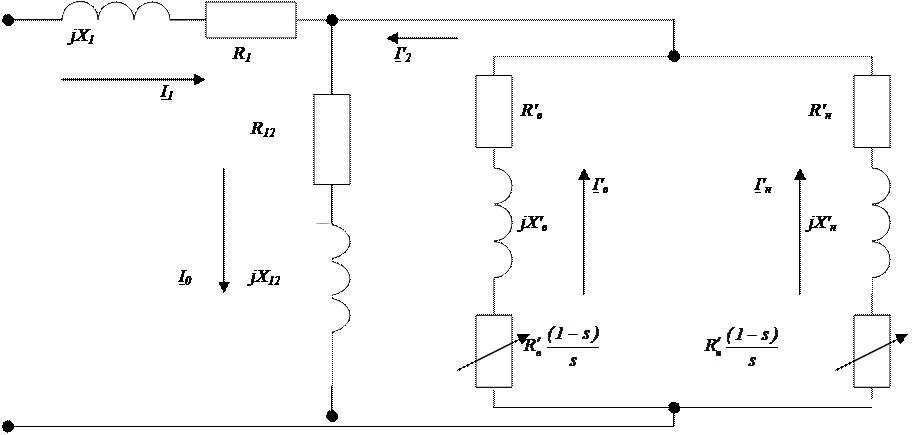 |
Рисунок 3 – Схема замещения асинхронного двигателя с двойной клеткой на роторе
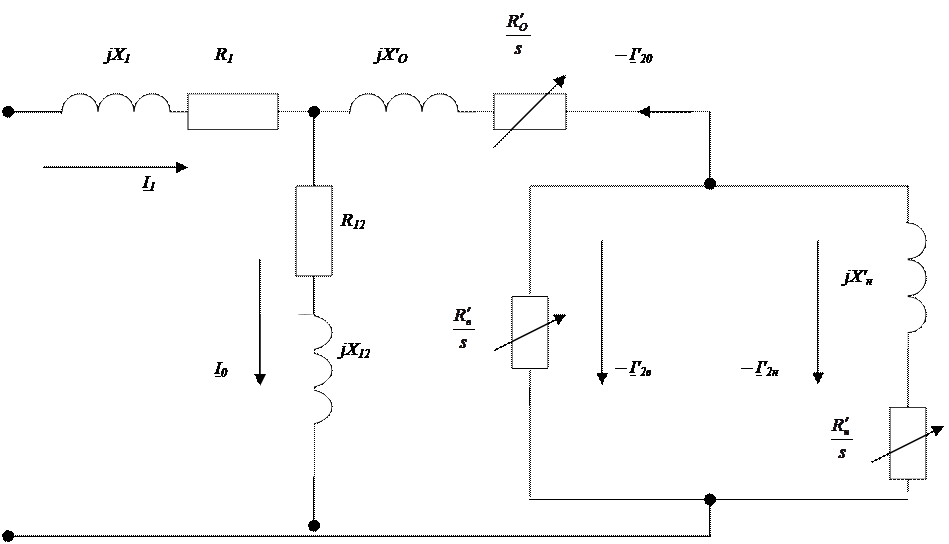 |
Рисунок 4 – Расчетная схема замещения двигателя с общим короткозамыкающим кольцом на роторе и без учета индуктивности рассеяния верхней клетки.
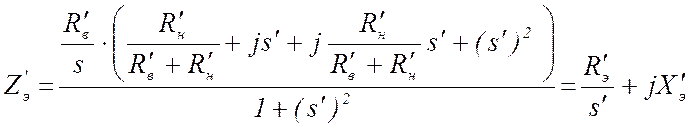 ,
(15)
,
(15)
а отсюда
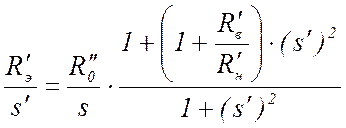 , (16)
, (16)
или
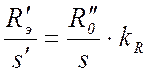 .
(17)
.
(17)
При этом
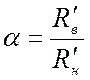 ,
(18)
,
(18)
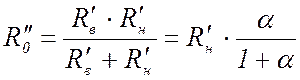 ,
(19)
,
(19)
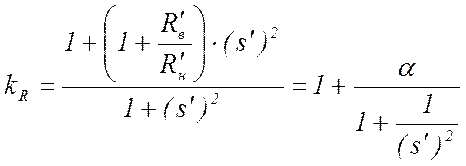 . (20)
. (20)
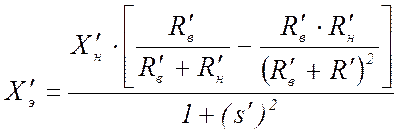 ,
(21)
,
(21)
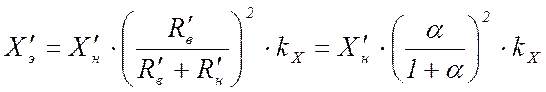 , (22)
, (22)
где
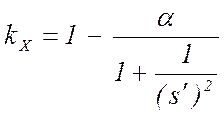 .
(23)
.
(23)
Далее определяются эквивалентные сопротивления роторной цепи при двойной клетке на роторе:
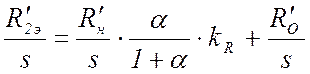 ,
(24)
,
(24)
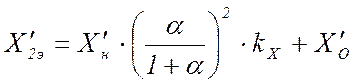 .
(25)
.
(25)
Таким образом, исследование машины с двойной клеткой на роторе может производиться при помощи уравнений (4) обычной машины. Следует, однако, иметь в виду, что сопротивления ротора будут зависеть от скольжения:
![]() и
и ![]() . (26)
. (26)
При решении дифференциальных уравнений (4) двухклеточного двигателя по методу Рунге – Кутта на каждом шаге интегрирования вычисляются скольжение и зависящие от него эквивалентные сопротивления ротора.
3 Программа работы и содержание отчета
3.1 Ознакомиться с дифференциальными уравнениями асинхронной машины с одной клеткой на роторе.
3.2 Ознакомиться с преобразованием параметров машины с двойной клеткой на роторе к параметрам, зависящим от скольжения.
3.3 Ознакомиться с алгоритмом решения дифференциальных уравнений по методу Рунге – Кутта.
3.4 Рассчитать переходный процесс для одного из асинхронных двухклеточных двигателей при различных значениях момента нагрузки (по указанию преподавателя).
3.5 По результатам расчета построить осциллограммы тока статора, момента, частоты вращения и скольжения в функции времени при различных значениях момента нагрузки.
3.6 Определить значения ударного тока и момента; определить время пуска двухклеточного двигателя при различных нагрузках.
3.7 Построить динамические механические характеристики М=f(s) для мгновенных значений при различных моментах нагрузки.
3.8 Рассчитать значения электрической ТЭ и электромеханической ТМ постоянных времени АД и проанализировать их влияние на характер переходного процесса.
4 Методические указания
4.1 К пункту 3.4
Исходные данные к расчету переходного процесса пуска двухклеточного асинхронного двигателя находятся в таблице 1.
Программа расчета реализована на языке Бейсик и находится в файле «QKIMB3t. bas». Программа позволяет вывести данные расчетов в различных опытах в текстовые файлы, отдельные для каждого опыта.
Порядок работы с программой:
Загрузить QBASIC, находящийся в файле «QBASIC. exe».
В среде QBASIC после нажатия клавиши Esc загрузить файл «QKIMB3t. bas». Для этого после нажатия клавиши Alt выбрать пункты меню FILE – OPEN, найти файл, отметить его курсором и нажать Enter. После этого на экране появится текст программы.
Запустить программу «QKIMBIDt. bas». Для этого нажать сочетание клавиш Shift+F5 или выбрать пункт меню RUN – START.
Провести расчет переходного процесса пуска двигателя в диалоговом режиме:
«Введите номер опыта (не более одного символа)» <ввести номер опыта>.
«Введите число уравнений N=» 5.
«Задайте начальный шаг Н=» 0.00166667.
«Задайте начальное ХО=» 0.
«Задайте начальное YО(1)=» 0.
«Задайте начальное YО(2)=» 0.
«Задайте начальное YО(3)=» 0.
«Задайте начальное YО(4)=» 0.
«Задайте начальное YО(5)=» 0.
«Отношение момента сопротивления к номинальному КМС=» <ввести относительное значение момента сопротивления>.
Далее по запросу ЭВМ вводятся параметры асинхронного двигателя из таблицы 1. Идентификаторы исходных данных:
MH – ЗНАЧЕНИЕ НОМИНАЛЬНОГО МОМЕНТА Мн, Н·м;
P – ЧИСЛО ПАР ПОЛЮСОВ p;
UH – НОМИНАЛЬНОЕ НАПРЯЖЕНИЕ Uн, В;
F1 – ЧАСТОТА ПИТАЮЩЕЙ СЕТИ f1, Гц;
NН – НОМИНАЛЬНАЯ ЧАСТОТА ВРАЩЕНИЯ nн, мин-1;
J – МОМЕНТ ИНЕРЦИИ, кг·м2;
X1 – ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ РАССЕЯНИЯ СТАТОРА X1, Ом;
XH – ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ НИЖНИХ СТЕРЖНЕЙ Xн', Ом;
XO – ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ ОБЩЕГО КОЛЬЦА XO', Ом;
RB – АКТИВНОЕ СОПРОТИВЛЕНИЕ ВЕРХНИХ СТЕРЖНЕЙRв', Ом;
RH – АКТИВНОЕ СОПРОТИВЛЕНИЕ НИЖНИХ СТЕРЖНЕЙ Rн', Ом;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.