Исследование переходных процессов в асинхронном двигателе c двухклеточным ротором: Методические указания к лабораторной работе № 7, страница 2

- момент механических потерь, равный 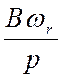, где В – коэффициент пропорциональности; момент трения качения в подшипниках может составлять значительную долю от номинального момента в машинах малой мощности; при моделировании АД средней и большой мощности приближенно можно считать, что этот момент при номинальной частоте вращения ротора равен 1% от номинального момента М_н

;

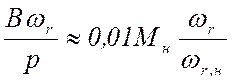большинство АД имеют вентилятор на валу; так как вентиляторный момент (как и момент трения ротора о воздух) является квадратичной функцией частоты вращения и он не велик по сравнению с другими слагаемыми уравнения момента, то можно считать при моделировании, что оба этих момента учитываются в результирующем моменте механических потерь;

- момент нагрузки М_с; в общем случае, М_с может быть произвольной функцией времени; при моделировании функция М_с(t) должна быть задана;

- электромагнитный момент двигателя М_э; как было отмечено выше, момент трения (механических потерь) входит в уравнение моментов в виде отдельного слагаемого; поэтому вращающий момент АД можно считать равным электромагнитному; последний определяется через мгновенные значения потокосцеплений, найденных в результате численного решения системы (4); уравнение электромагнитного момента для трехфазного АД имеет вид, Н·м:

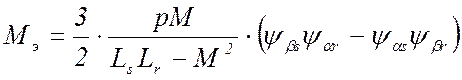.                           (5)

В результате дифференциальное уравнение моментов асинхронного двигателя запишется в следующем виде:

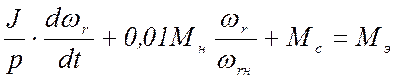               , или

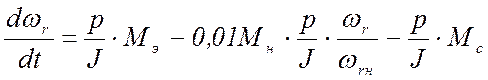.                           (6)

Взаимная индуктивность М связана с индуктивным сопротивлением взаимоиндукции между статором и ротором X₁₂ в схеме замещения:

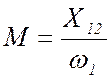.                                          (7)

Полные индуктивности фаз обмоток статора и ротора определяются суммой потокосцеплений с рабочим потоком и потоком рассеяния. Поэтому:

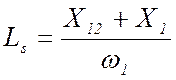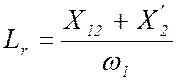;        ,                              (8)

где X₁ и X₂' – соответственно индуктивные сопротивления рассеяния обмоток статора и ротора из схемы замещения АД.

Активные сопротивления R_s и R_αr= R_βr=R_r в дифференциальных уравнениях не отличаются от сопротивлений фазы статора и ротора, входящих в схему замещения для установившегося режима, то есть при рабочей температуре берется R_s= R₁, R_r= R₂’.

2.2 Решение системы дифференциальных уравнений асинхронного

   двигателя численным методом Рунге – Кутта

Пусть требуется найти решение дифференциального уравнения y' = f(x,y), удовлетворяющего начальному условию y(x₀) = y₀. Численное решение задачи состоит в построении таблицы приближенных значений y₁ , y₂ ,… y_n и решении  уравнения y(x)  в точках  x₁ , x₂ ,… x_n. Точки x₁ , x₂ ,… x_n – узлы сетки. Для решения используется система равноотстоящих узлов. Величина h – шаг сетки (h>0).

Методом Рунге – Кутта в литературе обычно называют одношаговый метод четвертого порядка, относящийся к широкому классу методов данного типа. В рассматриваемом случае значения функции на каждом следующем шаге  y_i+1 вычисляются по формулам:

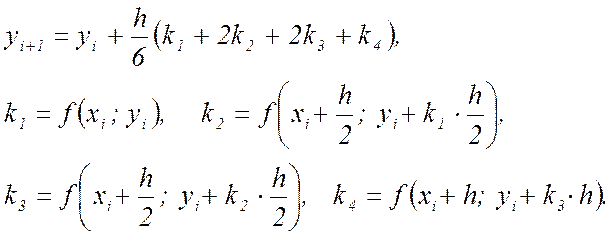                   (9)

Погрешность метода на одном шаге сетки равна mh⁵, но поскольку на практике оценить величину m обычно трудно, то при оценке точности используется правило Рунге. Для этого производится вычисление сначала с шагом h, а затем с шагом h/2. Если – приближение, рассчитанное с шагом h , а – приближение, рассчитанное с шагом h/2, то справедлива оценка:

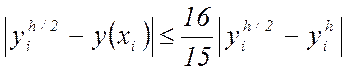.                                  (10)

При реализации метода на ЭВМ обычно на каждом шаге делается двойной перерасчет. Если полученные значения отличаются в пределах допустимой погрешности, то шаг h удваивается. В противном случае берется половинный шаг.

Метод Рунге – Кутта легко переносится на нормальные системы дифференциальных уравнений в виде:

,                     (11)

которые для краткости удобно записывать в векторной форме:

.        (12)

Для получения расчетных формул методом Рунге – Кутта достаточно в формулах (9) заменить y и f(x,y) соответственно на  и , а коэффициенты k_j на || k_j ||,  (j = 1, 2, 3, 4). Алгоритм метода Рунге – Кутта представлен на рисунке 1.

В данной работе величина шага интегрирования h принята равной 0,0016667 с, что составляет 1/12 периода напряжения при частоте 50 Гц.

Рисунок 1 – Алгоритм численного интегрирования системы дифференциальных уравнений по методу Рунге – Кутта

2.3 Переход от модели двухклеточного ротора к одноклеточному

Литая обмотка ротора с фигурным пазом для двухклеточного двигателя (приведенная на рисунке 2) может быть условно разбита на две части. Для них выполняется общее короткозамыкающее кольцо на обоих торцах ротора, причем одновременно с отливкой этих колец отливаются и вентиляционные лопатки. Параметры короткозамкнутого двигателя с двойной клеткой определяются в соответствии с его схемой замещения.

При этом предполагается, что в машине существуют основное поле, линии которого сцепляются со всеми тремя обмотками, и поля рассеяния обмоток.

Обмотку статора и обе клетки ротора – пусковую и рабочую – можно рассматривать как три магнитно-связанных контура.

Схема замещения двигателя с двойной клеткой на роторе приведена на рисунке 3. На схеме:  R_в^'и  R_н^' – активные сопротивления, X_в^'  и  X_н^' – индуктивные сопротивления, I_в'  и I_н'  – токи верхней и нижней клеток ротора, s – скольжение ротора.

Для упрощения расчетов осуществляется переход к схеме замещения. приведенной на рисунке 4. Она отличается от предыдущей тем, что здесь активное сопротивление короткозамыкающего кольца R'_O и его индуктивное сопротивление X'_O вынесены в цепь общего тока ротора.