Физический маятник
Цель работы: изучение гармонических колебаний; определение приведённой длины маятника и ускорения свободного падения.
Простейшим типом колебаний является горманическое колебание, когда смещение тела от положения равновесия зависит от времени по закону:
![]() или
или ![]()
Основные характеристики колебаний — амплитуда, частота, период. Частота колебаний равна числу полных колебаний, совершаемых за единицу времени. Периодом колебаний называется промежуток времени, за который совершается одно полное колебание. Период связан с частотой соотношением
![]()
Циклическая или круговая частота
колебаний численно равна числу полных колебаний, за ![]() секунд:
секунд:
![]() . Тело совершает гармонические
колебания, когда на него действует другая сила, пропорциональная величине
смещения от положения равновесия :
. Тело совершает гармонические
колебания, когда на него действует другая сила, пропорциональная величине
смещения от положения равновесия : ![]() , где k –
коэффициент упругости. Знак “минус” указывает, что возвращающая сила направлена
в другую сторону от направления смещения, то есть к положению равновесия.
, где k –
коэффициент упругости. Знак “минус” указывает, что возвращающая сила направлена
в другую сторону от направления смещения, то есть к положению равновесия.
Запишем для колеблющегося тела второй
закон Ньютона: ![]() или
или ![]()
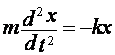 . Уравнение можно переписать
. Уравнение можно переписать 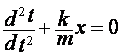 и ввести обозначения
и ввести обозначения ![]() . Тогда уравнение примет вид
. Тогда уравнение примет вид 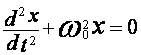 . Это и есть дифференциальное
уравнение гармонических колебаний. Одним из решений такого уравнения является
. Это и есть дифференциальное
уравнение гармонических колебаний. Одним из решений такого уравнения является ![]() . Циклическая частота колебания
. Циклическая частота колебания ![]() называется циклической частотой
собственных колебаний.
называется циклической частотой
собственных колебаний.
При гармонических колебательных движениях
кинетическая энергия колеблющейся материальной точки непрерывно меняется.
Меняется и потенциальная энергия взаимодействия между точкой и окружающей
средой. Кинетическая энергия колеблющейся точки массой 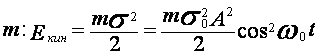 .
Потенциальная энергия квазиупругих сил, отсчитываемая от положения равновесия
данной материальной точки:
.
Потенциальная энергия квазиупругих сил, отсчитываемая от положения равновесия
данной материальной точки: 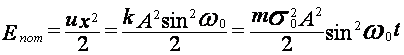 , где
, где ![]() - смещение колеблющейся точки от
положения равновесия,
- смещение колеблющейся точки от
положения равновесия, ![]() - коэффициент квазиупругой
системы. Полная энергия материальной точки, совершающей гармонические колебания
с частотой
- коэффициент квазиупругой
системы. Полная энергия материальной точки, совершающей гармонические колебания
с частотой ![]() и амплитудой A:
и амплитудой A:
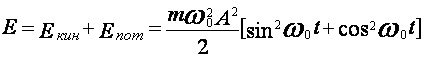
В процессе движения происходит
непрерывный переход кинетической энергии в потенциальную и обратно, но полная
энергия – величина постоянная, она пропорциональна квадрату колебаний.
Собственные гармонические колебания – это идеальный случай колебаний, когда
энергия системой не теряется, и амплитуда остается постоянной. В случае
реальных колебаний энергия, переданная системе, постепенно расходуется на
преодоления сил сопротивления, поэтому амплитуда колебаний уменьшается, колебания
затухают, эти колебания называются затухающими. Их частота определяется
свойствами колеблющейся системы – возвращающей силой, сопротивлением. Если сила
сопротивления среды пропорциональна скорости колебания, т.е. 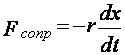 , 2 закон Ньютона для колеблющейся
точки запишем так:
, 2 закон Ньютона для колеблющейся
точки запишем так: 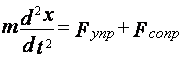 или
или 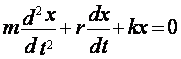 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.