Определение приведённой длины маятника и ускорения свободного падения, страница 2

Введем обозначения: . Решение уравнения имеет вид . Амплитуда затухающих колебаний уменьшается по закону , частота затухающих колебаний .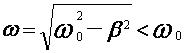

Если , частота является минимальным числом и имеет место апериодический процесс.

В случае затухающих колебаний энергия убывает по закону .

Влечена отношения энергии и мощности потерь за время . Характеризует способность колебательной системы хранить энергию и называется добротностью: .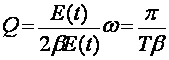

Добротность равна числу колебаний за время, за которое амплитуда уменьшается в раз.

   Для изучения колебаний можно использовать физический или математический маятник.

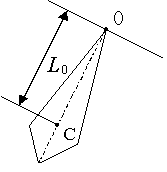
Каждое тело подвешенное в точки, лежащей выше его центра тяжести, может колебаться и представляет собой физический маятник. На рисунке изображен физический маятник, отклоненный от положения равновесия. Через точку О перпендикулярную плоскости рисунка проходит неподвижная ось, вокруг которой совершаются колебания. С – центр тяжести маятника (точка в которой приложена сила тяжести mg). Момент силы mg относительно оси О равен: , где  - расстояние от оси вращения до центра тяжести – точки С.

При малых углах отклонения, когда можно принять , основной закон динамики, вращательного движения, описывающий колебания такого маятника, можно записать в виде:

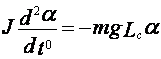 или 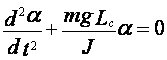,        где J – момент энергии физического маятника относительно оси вращения.

Это уравнение аналогично уравнению 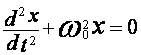, величина  является квадратом круговой частоты гармонических колебаний:

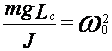
Решением уравнения  описывает гармонические колебания, совершаемые физическим маятником. Период колебаний: .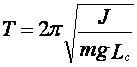

Для математического маятника 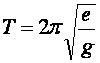. Физический маятник колеблется так же (с тем же периодом), как и математический, описываемый 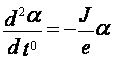, имеющий длину , где  от 0 до с.

Приведенная длина  физического маятника, который имеет тот же период колебаний, что и данный физический маятник.

Если к оси физического маятника подвесить грузик на нити такой длины, чтобы она была ровна приведенной длине такого физического маятника, то отклоненные на одинаковый угол физический маятник и грузик колеблются вмести так, что грузик находится в одной и той же точки физического маятника – его центр качания. Поэтому приведенная длина будет 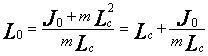, т.е..