Определение приведённой длины маятника и ускорения свободного падения, страница 3

Методика проведения эксперимента

   Обратный маятник состоит из стального стержня, на котором закрепляются опоры 1 и 2 в виде призм и грузы 3 и 4. Время N полных колебаний маятника измеряются секундомерами. В автоматическом режиме секундомер включается при срабатывании фотоэлемента датчика 6, выключается кнопкой СТОП.

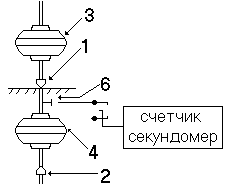
Метод оборотного маятника основан на сопряженности двух его точек: подвеса и центра касания. Путем изменения расстояния между грузами (перемещением груза 3) добиваются такого расстояния, чтобы период колебания маятника при его переворачивании не менялся. При этом расстояние между опорами будет приведенной длиной маятника .

Теоретически рассчитать положение центра масс физического маятника можно для упрощении модели маятника, состоящей из невесомого стержня с закрепленным на нем материальными точками 3 и 4.

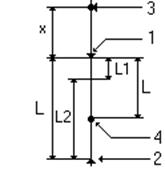Порядок выполнения работы

Исходные данные:

Расстояние между спорами L=0.312м

Расстояние от опоры 1 до груза 4 l=0.15м

Масса маятника m=1.4м

Будем передвигать груз 3 и измерять время 12 полных колебаний, а результат записывать в таблицу, в которой:

x – расстояние от груза 3 до опоры 1

t1 – время 12 полных колебаний маятника, подвешенного за опору 1

t2 – время 12 полных колебаний маятника, подвешенного за опору 2.

№ эксперимента	х, м	t1, c	T2, c
1	0.04	12.60	13.10
2	0.05	13.02	13.50
3	0.06	13.30	13.50
4	0.07	14.61	14.50
5	0.08	14.83	14.34

Построим зависимость времени колебаний маятника на опорах 1 и 2 от положения груза 3.

По точки пересечения графиков находим   хпр=0.0625м.

Приведенная длина физического маятника определяется по формуле: .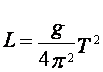

Необходимо найти . Для этого установим груз 3 в положение хпр=0.062м и определим время 12 колебаний 12 маятника, повторим опыт несколько раз: