13) ТестКеттела . ., .
14) Личностная тревожность
15) Тест Айзенка
16) ТестЛюшера
За основной тест при определении надежности и стартоготовности в КСПДС принят тест Кеттела.
Подход Кеттела основан на том, что личностные черты составляют ядро структуры личности и, в конечном счете, отвечают за то, что будет делать индивидуум в прогнозируемой ситуации. Теория черт личности Кеттела базируется на основе статистического анализа объективны?! поведенческих реакций. Согласно Кеттелу предсказание поведения (специфической ответной реакции индивидуума -R) может быть осуществлено посредством уравнения спецификации [139]:
![]()
где S - неопределенная функция от стимулирующей ситуации в конкретный момент времени;
Р - неопределенная функция от структуры личности.
Уравнение спецификации показывает, что характерная реакция на какую-либо ситуацию представляет собой функцию от комбинации всех черт, значимых
чанной ситуации, присущих и откорректированных для той или иной степени оииональной возбудимости индивидуума.
Для анализа оценок распределения тестовых баллов, принятия тестовых
у и проверки их репрезентативности используются показатели валидности и
жности свойств какого-либо теста или их комбинаций. Под надежностью теста
«имается отношение истинной дисперсии к дисперсии эмпирически
зарегистрированных баллов [200]:
![]()
При этом общий разброс (дисперсия) результатов произведенных измерений представляется как сумма двух источников: самого измеряемого свойства и наличия ошибки измерения, вызванной действием внешних помех и проявлением степени неопределенности как каждого пункта теста, так и индивидуальности тестируемого.
Определение ошибки измерения осуществляется корреляционными методами, позволяющими определить точность (надежность) на основе ретестовой устойчивости (повторного проведения теста спустя значительное время (более двух недель).
Для интервальных шкал, по которым определяются психические характеристики, относительно устойчивые во времени, коэффициент корреляции определяется [200]:
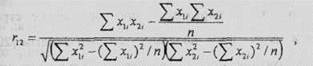
где X/i - тестовый балл -того испытуемого при первом измерении: x2i - тестовый балл того же испытуемого при повторном измерении; п - количество испытуемых.
Высокая надежность достигается тогда, когда дисперсия ошибки оказывается пренебрежительно малой. Относительную долю дисперсии ошибки можно установить из соотношения:
![]()
Обычно в тестологической практике редко удается достичь коэффициентов, превышающих 0,7-0,8. Для определения истинного значения тестового бадла тестируемого используется следующая формула:
*«,=гх,+(\-г)х,(5.19)
где Хш - истинный балл;
X, эмпирический балл;
Т эмпирически измеренная надежность теста,
X среднее для теста.
В отличие от технических систем ретестовая надежность измерений зависит не только от периода времени между измерениями, но и заполненности зафиксированного периода времени значимыми для индивидуума событиями, т.е. у испытуемого быстрее изменится состояние, чем они забудут свои ответы по предыдущему тестированию.
Известно, что надежность методики всегда больше ее ваяидности и высокая устойчивость тестового показателя на длительном промежутке времени совершенно не означает получение значимых линейных корреляций тестового показателя с требуемым критерием валидности.
Как правило, на основе диагностики принимаются решения, которые соотносятся между собой как события на шкале наименований (ранга или порядка) и линейные (статистическая экстраполяция результатов тестирования на заданном промежутке времени). Линейные и порядковые прогностические стратегии на практике применяются не к одномерным, но к многомерным данным [200]. Среди математических моделей прогнозирования до сих пор наибольшей популярностью пользуются относительно простые регрессионные модели.
|
|
|
где Y - прогнозируемая переменная (критерий прогностической валидности); |
При этом для многомерного случая задача психометриста сводится к построению множественной регрессии:
ДГ, - значение (-того тестового показателя из рассматриваемой батареи тестовых показателей;
Р, - значение весового коэффициента, указывающего на сколько (в единицах стандартных отклонений) изменяется прогнозируемая переменная при изменении тестового показателя -л,-
Для построения указанного уравнения требуется произвести "упреждающее" измерение тестовых показателей по отношению к критериальному показателю У, измерение которого производится по истечении некоторого отрезка времени ЛГ, называемого в прогнозировании периодом упреждения.
Общая эффективность прогноза на основе регрессионного уравнения оценивается с помощью подсчета коэффициента множественной корреляции R и последующей оценки его значимости по критерию Фишера:
![]()
где Ft - эмпирическое значение статистики Фишера со степенями свободы Vx = к hV2= N -к,
N - количество индивидов; к - количество тестовых показателей.
Основой применения этой модели прогноза является экстраполяция, т.е. предположение о том, что на новом отрезке времени Т будут действовать те же тенденции связи переменных, что и на отрезке Т, на котором прежде измерялись весовые коэффициенты.
Применению методики опроса Кеттела с целью интерпретации факторов предшествовали процедуры выявления экспертных оценок по всем шкалам: - "замкнутость - общительность"; " "интеллект",
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.