Візуалізація соціологічної інформації. Статистичні висновки: статистичне оцінювання. Статистичний вивід: статистична перевірка гіпотез, страница 6

Статистична значущість розбіжностей

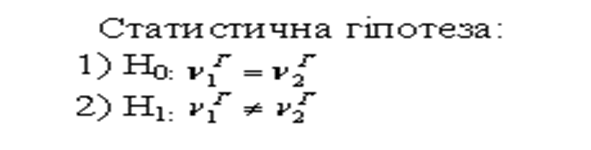
З математичної статистики відомо, що на 5%-му рівні значущості критичні точки статистики z дорівнюють - 1,96 і +1,96, а на 1%-ному - 2,58 і +2,58. Область, що лежить між критичними точками, є областю прийняття гіпотези, а поза цими точками – критичною областю. Якщо, наприклад, підставивши отримані в емпіричному дослідженні дані у формулу (**), ми одержали, що -1,95< z <1,96, то гіпотеза Нo приймається, а якщо z=1,96 або z=-1,96, то гіпотеза відкидається на 5%-му рівні значущості.

              У пакеті ОСА застосовано саме такий підхід: розрахунки виконуються за наведеними формулами, а перевірка гіпотези виконується на двох стандартних для соціальних наук рівнях значущості – 5% та 1%.

Література

n Бююль А., Цёфель П. SPSS: искусство обработки информации. Анализ статистических данных и восстановление скрытых закономерностей. – СПб.: ООО «ДиаСофтЮП», 2002. – С. 157-161, 192-193, 250-253.

n Наследов А. SPSS: компьютерный анализ в психологии и социальных науках. – Питер, 2005. – С. 380-387.

n Паніотто В.І., Максименко В.С., Марченко Н.М. Статистичний аналіз соціологічних даних. – К.: Вид.дім “КМ Академія”, 2004. – С. 65-80, 201-206).

n OCA Учебник online. – Доступно на: http://www.oca.com.ua/

Кислова О. М. Курс «Методи аналізу соціологічної інформації»

Аналіз розбіжностей середніх

Повторення: резюме попередньої лекції

Аналіз розбіжностей застосовується для порівняння результатів дослідження двох (або більшої кількості) груп з метою визначення ступеня реальної відмінності в їхній поведінці, ціннісних орієнтаціях, електоральних настроях тощо.
      Кількісним показником такої відмінності є статистична значущість розбіжності.

Для розрахунку статистичної значущості розбіжностей існує велика кількість тестів, серед яких аналітик повинен обрати адекватний досліджуваним даним.

•  Для розрахунку статистичної значущості розходжень існує велика кількість методів, серед яких аналітик має обрати адекватний досліджуваним даним.

•  Вибір методу перевірки статистичної значущості розходжень визначається обсягами вибірок (досліджуваних груп), типом шкали аналізованої ознаки, формою її розподілу (нормальністю або ненормальністю),  залежністю/незалежністю вибірок та кількістю вибірок (дві або більше)

•  Тип шкали визначає, буде соціолог порівнювати відсотки чи середні значення.

•  Форма розподілу аналізованої ознаки, тобто відповідність чи невідповідність нормальному розподілу обумовлює  застосування параметричних чи непараметричних тестів.

•  Залежність або незалежність вибірок також впливає на вибір методу перевірки статистичної значущості розбіжностей. Існують окремі методи для залежних та незалежних вибірок.

•  Кількість вибірок. Для двох вибірок застосовують одні методи (наприклад, Т-тести). Коли ж порівнюємо одночасно більше за дві вибірки, то не всі тести можна застосовувати, але існують спеціальні методи призначені сама для таких випадків – дисперсійний аналіз.

1.  Вибір тесту для перевірки статистичної значущості розбіжностей залежить від типу шкали аналізованих ознак
 Від типу шкали залежить, будемо ми застосовувати середні значення чи проценти при порівнянні певних характеристик досліджуваних груп.

2.  .     Вибір тесту для перевірки статистичної значущості розбіжностей середніх залежить від того, чи є розподіл аналізованої ознаки нормальним.

 Від нормальностіабо ненормальності розподілу залежить, будемо ми застосовувати параметричні чи непараметричні тести при порівнянні певних характеристик досліджуваних груп.

Параметричні та непараметричні критерії розбіжностей

•  Критерій розбіжності називають параметричним, якщо він ґрунтується на наявному вигляді розподілу генеральної сукупності (як правило, нормальному), використовує параметри цієї сукупності (середні, дисперсії тощо).

•  Критерій розбіжності називають непараметричним, якщо він не базується на припущенні щодо виду розподілу генеральної сукупності та не використовує параметри цієї сукупності.

•  Параметричні критерії мають більшу потужність у порівнянні з непараметричними, вони здатні з більшою вірогідністю відкидати нульову гіпотезу, якщо вона невірна. Тому у випадках, коли вибірки взято з нормально розподілених генеральних сукупностей, варто віддавати перевагу параметричним критеріям.

•  Проте практика показує, що розподіл переважної більшості даних, одержуваних у соціологічних опитуваннях, не відповідає нормальному розподілу, тому застосування параметричних критеріїв для аналізу результатів соціологічних досліджень може призвести до помилок у статистичних висновках. У таких випадках зазвичай застосовують непараметричні критерії.

•  Вибір тесту для перевірки статистичної значущості розбіжностей середніх залежить від того, залежні або незалежні порівнювані нами вибірки.

 Існують окремі методи перевірки статистичної значущості розбіжностей для залежних та незалежних вибірок.

Незалежні та залежні (парні) вибірки

•  Якщо можна встановити гомоморфізм (тобто відповідність, коли одному випадку з вибірки X відповідає один і тільки один випадок з вибірки Y і навпаки) для кожного випадку у двох вибірках, то такі вибірки називаються залежними або парними.

•  Залежні вибірки характеризуються кореляцією думок респондентів, які утворюють пару.

•  У соціологічних дослідженнях застосовують тести для парних вибірок, коли порівнюють різницю у відповідях на різні запитання однієї групи респондентів.

•  У випадку відсутності взаємозв'язку між вибірками вони вважаються незалежними. В соціологічних дослідженнях дві вибірки (дві різні групи респондентів) практично завжди є незалежними.

Приклади залежних (пов’язаних) вибірок:

² пари близнюків;

² чоловіки й дружини;

² два виміри якої-небудь ознаки до й після експериментального впливу.

Приклади незалежних (непов’язаних) вибірок:

² чоловіки й жінки;

² соціологи й математики;

² мешканці Харкова та мешканці Києва.

Вибір методу для перевірки статистичної значущості розбіжностей середніх залежить також від кількості  порівнюваних вибірок.

 Для двох вибірок застосовують одні методи (наприклад, Т-тести або критерій Манна-Уітні). Коли ж порівнюємо одночасно більше за дві вибірки, то не всі тести можна застосовувати, але існують спеціальні методи призначені сама для таких випадків – дисперсійний аналіз.