



















1. Классификация СУЭП: по виду цепи воздействия и принципу построения.
По виду цепи воздействия: системы с разомкнутой(отсутствуют обратные связи) и замкнутой(повышение точности управления) цепью воздействия.
По принципу построения:
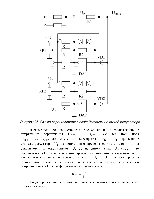
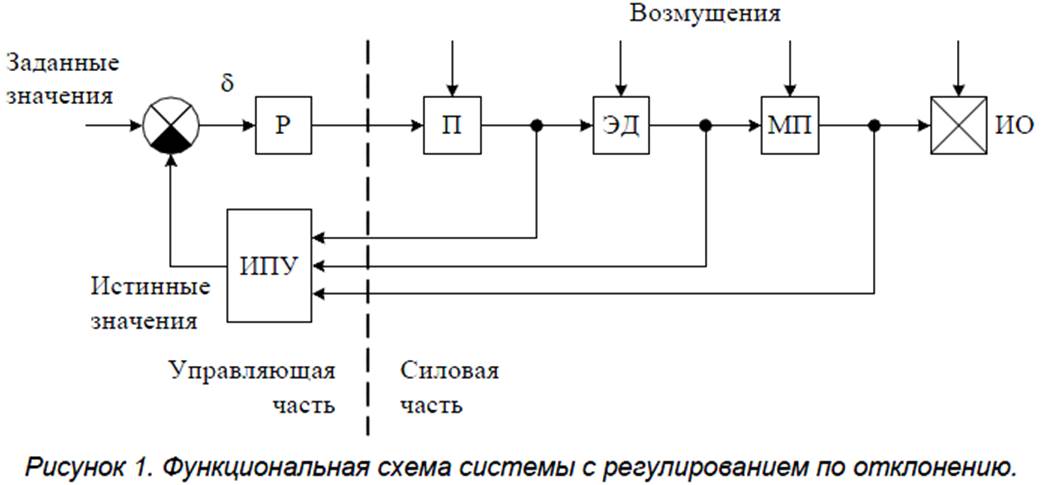
1. Системы с регулированием по отклонению.
Регулятор Р и измерительно-преобразовательное устройство ИПУ образуют управляющую часть (УЧ). В силовую часть (СЧ) входят: управляемый преобразователь УП, электродвигатель ЭД, механическая передача МП. ИО – исполнительный орган. δ – сигнал ошибки.
2. Системы с комбинированным управлением обеспечивают уменьшение или полное устранение ошибки по окончанию переходного процесса.
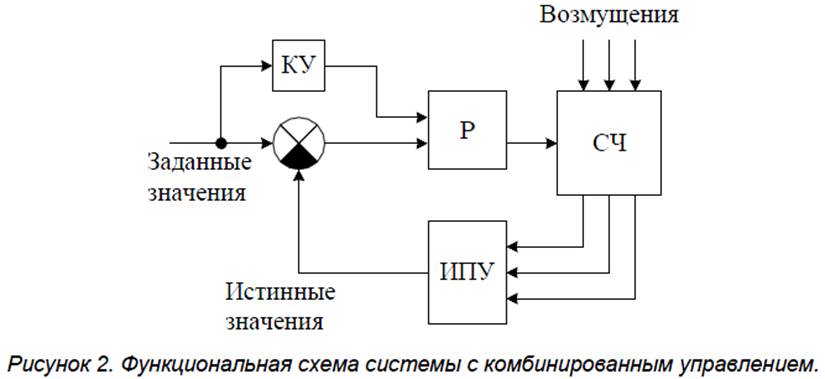
При отсутствии возмущений и стабильных параметрах СЧ компенсационное устройство КУ обеспечивает подачу на вход регулятора дополнительного сигнала для компенсации ошибки переменных.
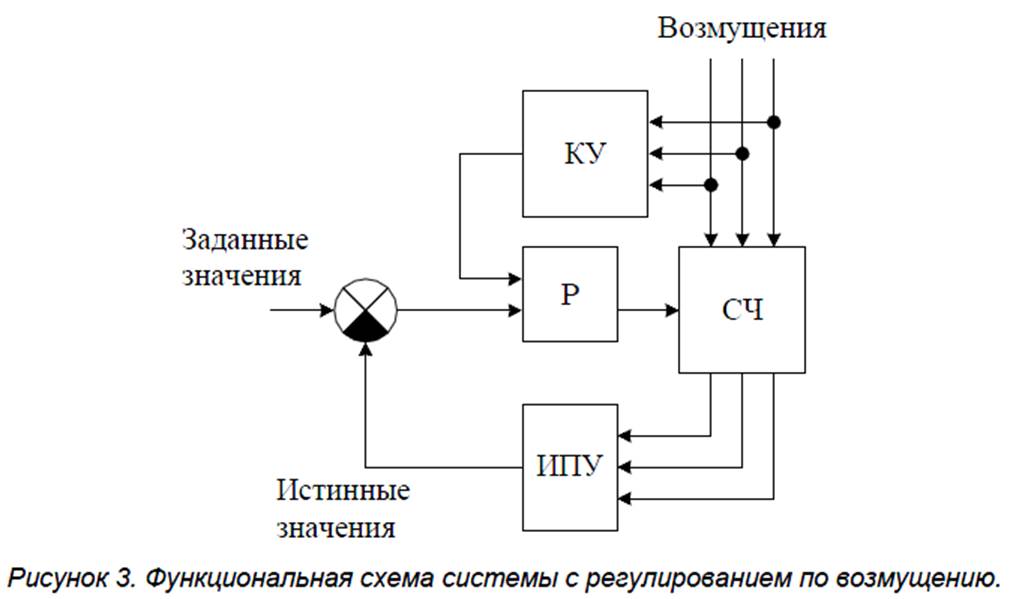
3. Инвариантные системы (системы с регулированием по возмущению) позволяют уменьшить, а в идеальном случае полностью устранить ошибки от возмущений.
Устройство компенсации КУ обеспечивает измерение возмущений и вырабатывает сигналы для компенсации их воздействия.
Классификация СУЭП: по основной выполняемой функции (по основной выполняемой функции).
Можно выделить 7 групп систем:
1. Обеспечивает пуск, торможение и реверс при питании двигателя от сети.
2. Аналогична первой группе, но производиться формирование переходных процессов с помощью логического управления со ступенчатым воздействием на двигатель, например переключение резисторов.
3. Обеспечивает оптимальные процессы пуска, торможения и реверса с точки зрения быстродействия при условии ограничения тока или момента.
4. Обеспечивают задание и автоматическую стабилизацию (введение обратной связи по
соответствующей переменной) скорости или другой координаты.
5. Осуществляют следящее управление, получение требуемой координаты (обычно положение и скорость) с требуемой точностью.
6. Обеспечивают автоматическое управление ЭП по заранее заданной программе.
7. Системы, обеспечивающие выбор наилучших режимов работы электроприводов в случае непредвиденного изменения возмущающих воздействий. Такие системы называют адаптивными или оптимальными.
2. Математический аппарат.
СУЭП описываются системами нелинейных дифференциальных уравнений, которые характеризуют зависимости переменных системы друг от друга и от входных воздействий.
Дифференциальные уравнения обычно используют в нормальной форме Коши. применяют структурные схемы. При сложных системах, систему дифференциальных уравнений представляют в матричной форме и используют матричные структурные схемы. Для облегчения анализа и синтеза линеаризованных систем применяют операторные уравнения. Воспользоваться указанными методами математического аппарата при аналитическом решении можно, если нелинейности гладкие и допускают линеаризацию, либо не оказывают существенного влияния на работу системы управления. Когда нелинейности не гладкие (релейная характеристика, петля гистерезиса, люфт, насыщение и т.д.) используют метод гармонической линеаризации, или численные методы решения систем дифференциальных уравнений. Также, для упрощения записи в ряде случаев используют относительные величины, т.е. нормирование.
Линеаризация нелинейных дифференциальных уравнений: порядок применения.
Под линеаризацией понимают замену нелинейных членов дифференциальных уравнений линейными. При этом используют следующие приемы:
1. Линейная аппроксимация, т.е. замена нелинейных характеристик элементов систем линейными (кривая намагничивания, угловая характеристика синхронной машины).
2. Пренебрегают нелинейными членами из-за их малости (например при расчете сопротивления якорной цепи СУЭП постоянного тока пренебрегают сопротивлением щеточно-коллекторного контакта).
3. Используют разложение в ряд Тэйлора. Данный прием позволяет избавиться от произведения переменных.
Разложение в ряд Тэйлора применяется в следующем порядке:
1. Определяется начало и направление отсчета каждой из переменных.
2. Записывается система нелинейных дифференциальных уравнений.
3. Определяются значения координат для установившегося рабочего режима X и задаются малые приращения переменных в процессе регулирования ∆x .
4. Производиться линеаризация путем подстановки в уравнения значений переменных, представленных в виде суммы установившегося значения и малого приращения x= X+∆x . При этом появляются слагаемые 3 типов:
4.1.X∙X, относящиеся только к описанию статических режимов.
4.2.X∙∆x,где установившееся значение переменной - в роли постоянного коэффициента.
4.3.∆x ∙ ∆x , которыми пренебрегают из-за их малости.
5. Записывают линеаризованную систему уравнений но уже в отклонениях переменных.
6. По линеаризованной системе уравнений строится структурная схема.
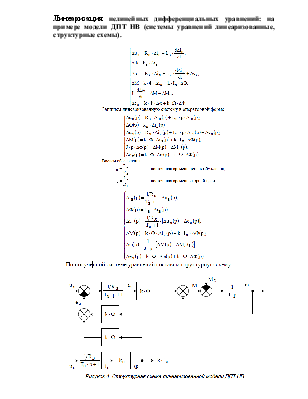
Линеаризация нелинейных дифференциальных уравнений: на примере модели ДПТ НВ (уравнения исходные, процесс линеаризации уравнений для цепи якоря и момента, система уравнений линеаризованная).
Исходная система уравнений
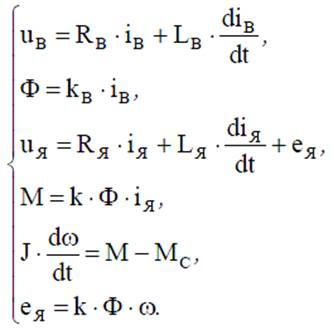
линеаризация уравнений для цепи якоря и момента
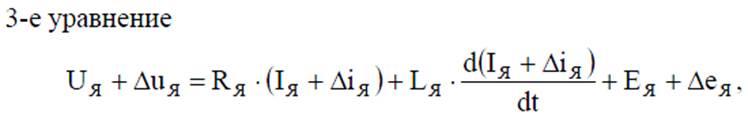
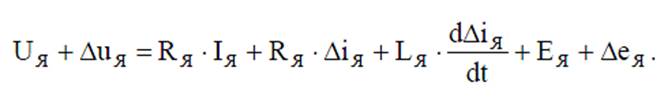
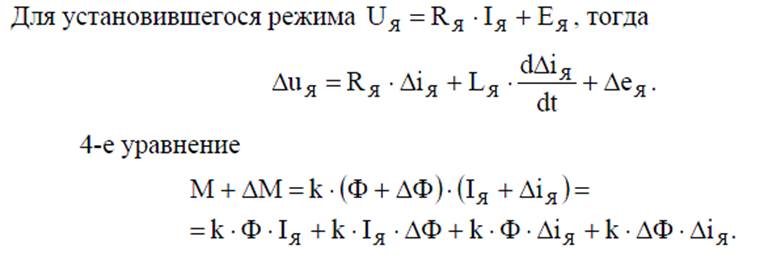
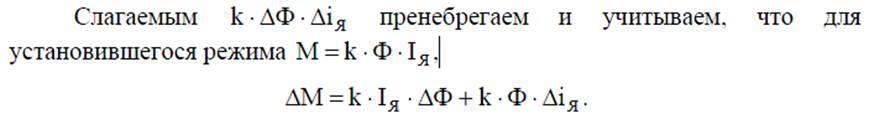
система уравнений линеаризованная
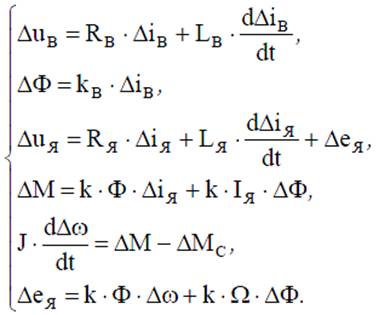
Линеаризация нелинейных дифференциальных уравнений: на примере модели ДПТ НВ (системы уравнений линеаризованные, структурные схемы).



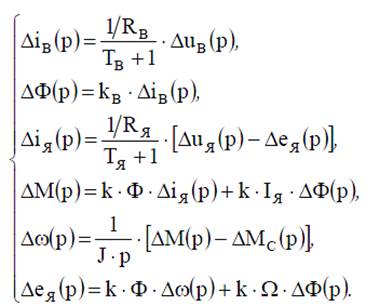
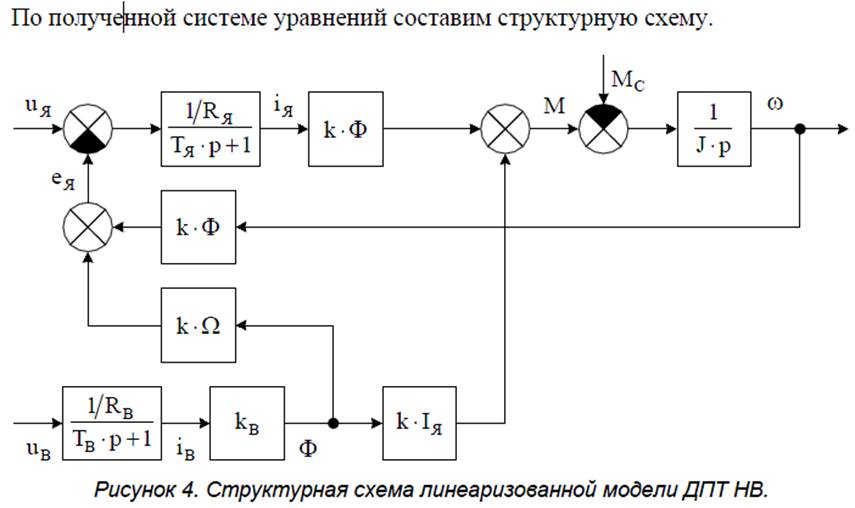
3. Математическое описание линеаризованных систем: структурная схема, пространство состояний, форма Коши.
Структурная схема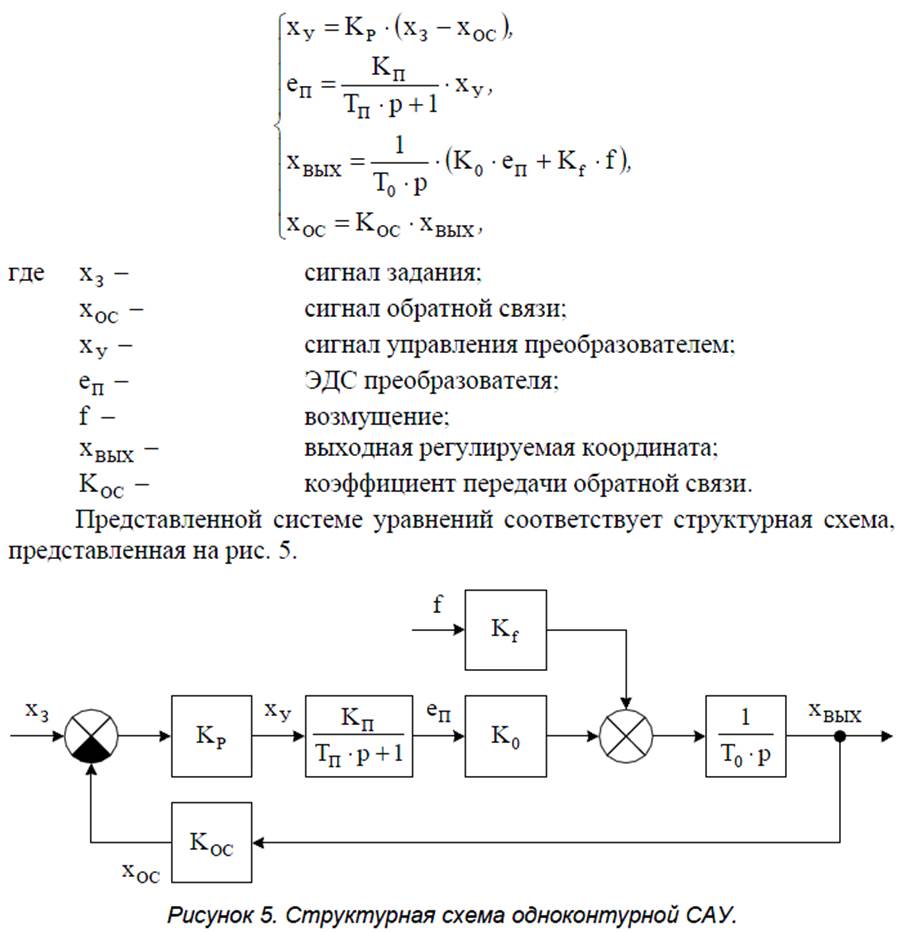
пространство состояний
Т.е. состояние САУ n-го порядка в любой момент времени можно охарактеризовать изображающей точкой в n-мерном пространстве. Координатами пространства являются выходные переменные динамических элементарных звеньев. Для рассматриваемой САУ 2-го порядка координатами пространства будут переменные eп и xвых . Представлению в пространстве состояний соответствует запись дифференциальных уравнений в нормальной форме Коши.
форма Коши
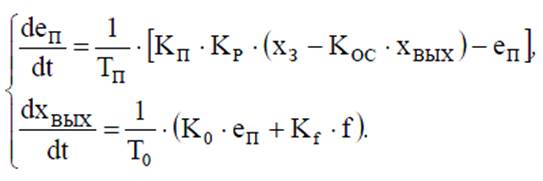
Математическое описание линеаризованных систем: относительные единицы.
Обычно для достаточно сложных систем с целью уменьшения количества коэффициентов, упрощения записи и увеличения наглядности используют нормирование, т.е. переход к относительным единицам. Если какое-то значение выходной переменной принять за базовое XВЫХ.Б, то можно определить базовые величины для остальных переменных
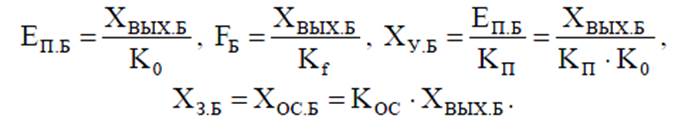
![]() – относительный коэффициент передачи регулятора.
– относительный коэффициент передачи регулятора.
В итоге
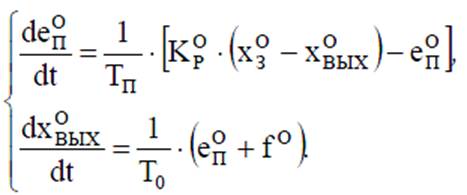
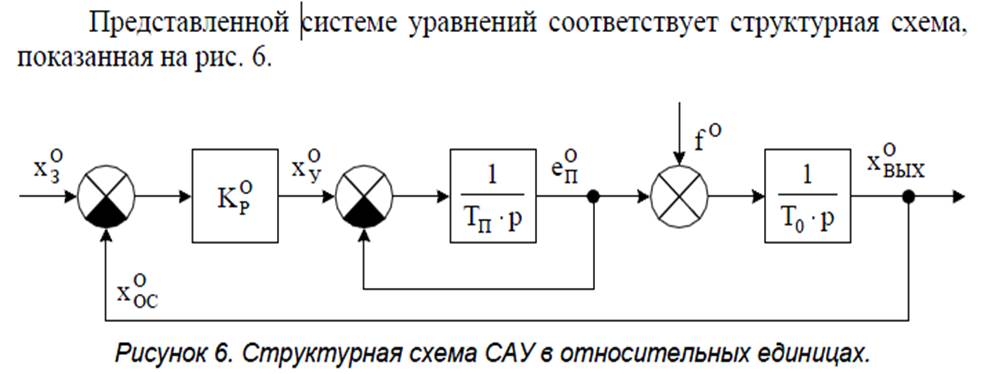
Математическое описание линеаризованных систем: векторно-матричная
форма.
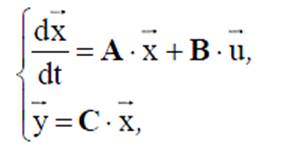



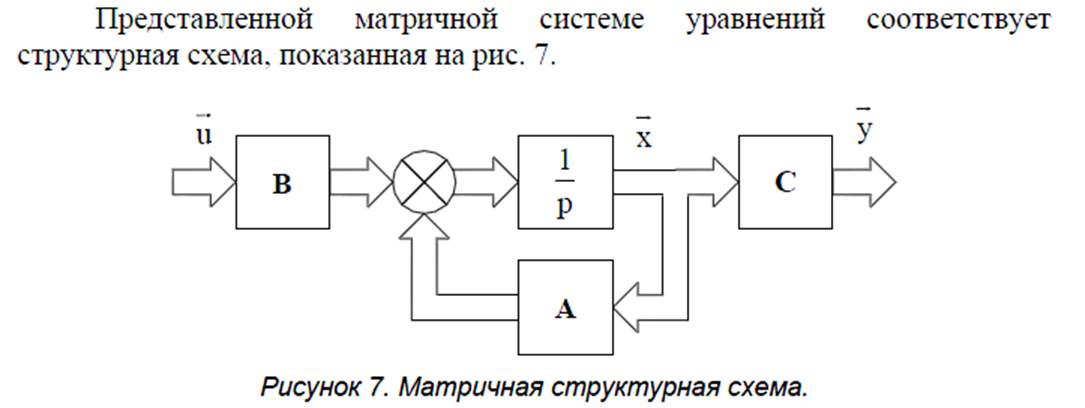
4. Методы синтеза СУЭП.
Сам синтез заключается в выборе структуры САУ, схемы и параметров регулирующих устройств. Конечной целью синтеза является обеспечение электроприводом статических и динамических показателей.
В зависимости от общего подхода к синтезу систем, формирование статических и динамических свойств можно рассматривать как единую или как две различные задачи. В последнем случае, для получения значения какой-либо переменной с заданной статической точностью при регулировании используется либо отрицательная обратная связь по этой переменной, либо обратная связь для компенсации возмущения, влияющего на переменную.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.