Формирование требуемых динамических свойств, т.е. синтез систем по динамическим показателям является обратной задачей анализа динамики. По заданным показателям выбирается вид переходного процесса, желаемая логарифмическая характеристика или желаемое распределение корней характеристического уравнения. Затем на основе их сравнения с характеристиками или корнями имеющейся структуры выбирают
корректирующие динамические звенья.
На практике чаще всего применяют 3 метода синтеза:
1. Частотный метод.
2. Метод оптимизации контуров регулирования.
3. Метод аналитического конструирования.
Наиболее удобным при расчетах и наладке системы управления является метод оптимизации контуров регулирования.
5. Стандартные настройки контуров: технический оптимум.
Рассмотрим простейший контур регулирования (в относительных единицах при единичной обратной связи).
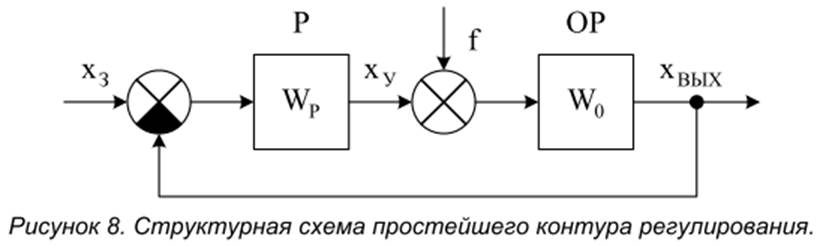
Где
Р - регулятор с передаточной функцией ![]() ;
;
ОР - объект регулирования с передаточной функцией ![]() .
.
Передаточная функция замкнутого контура
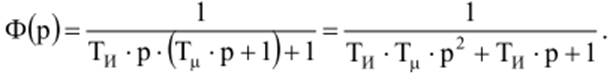
Обозначим
![]() С точки зрения
перерегулирования, времени переходного процесса и колебательности наилучший
вариант обеспечивается при m
= 2 . Тогда
С точки зрения
перерегулирования, времени переходного процесса и колебательности наилучший
вариант обеспечивается при m
= 2 . Тогда
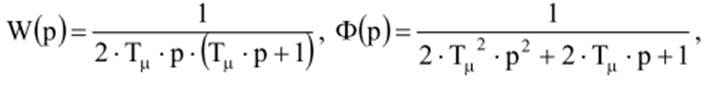
и
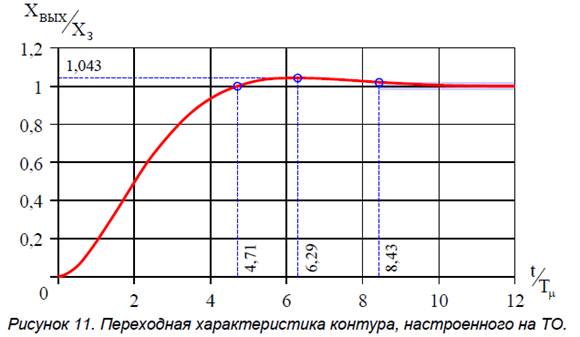
контур представляет собой колебательное звено с коэффициентом затухания ![]() . Логарифмическая и
переходная характеристики контура приведены на рис. 10 и 11.
. Логарифмическая и
переходная характеристики контура приведены на рис. 10 и 11.

Стандартные настройки контуров: симметричный оптимум.
Логарифмическая характеристика такого контура представлена на рис. 13. Данный способ настройки получил название симметричного оптимума.
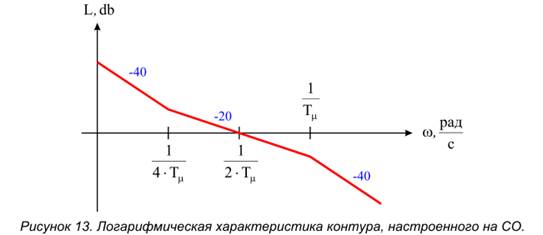
Переходной
процесс по управлению в таком контуре протекает со значительным
перерегулированием ![]() , вызываемым, в основном, наличием
форсирующего звена. Длительность переходного процесса составляет
, вызываемым, в основном, наличием
форсирующего звена. Длительность переходного процесса составляет ![]() .
.
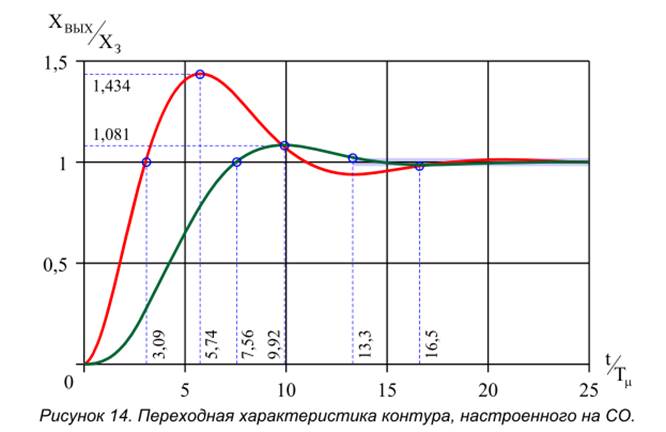
На рис. 14 изображены переходные процессы контура по управлению при отсутствии и при наличии фильтра на входе.
Итак, для настройки контура регулирования на технический оптимум необходимо получить передаточную функцию контура регулирования
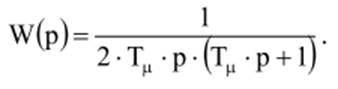
При интегрирующем объекте регулирования для исключения ошибки контура по возмущению можно настроить контур на симметричный оптимум, добавив в передаточную функцию регулятора, настроенного на ТО ПИ-звено
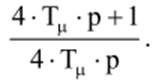
Тогда передаточная функция контура будет иметь вид
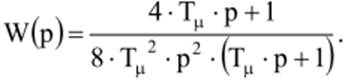
Т.е. производится оптимизация по статической ошибке по возмущению.
6. Обзор стандартных настрое контуров.
Пусть общий вид уравнения
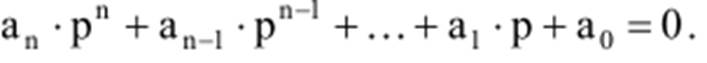
Введем оператор s
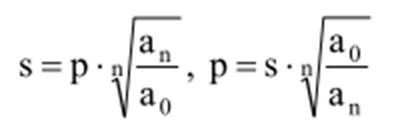
и подставим в уравнение
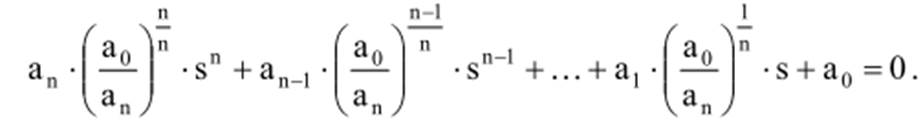
Разделив
на ![]() , получим
, получим
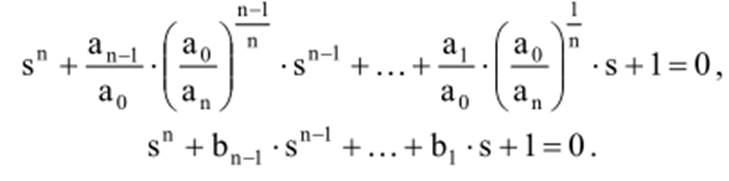
Нормирование подобным образом характеристического уравнения равносильно применению нормирующей базовой частоты
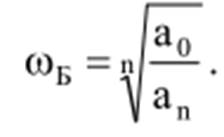
Относительное время при этом
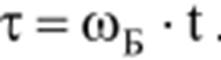
7. Понижение расчетного порядка контура регулирования.
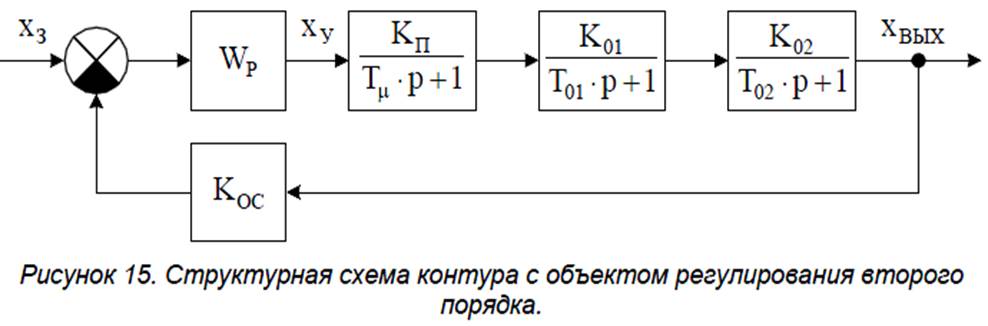
Контур
содержит регулятор с передаточной функцией ![]() , управляемый преобразователь УП с
суммарной малой постоянной времени
, управляемый преобразователь УП с
суммарной малой постоянной времени ![]() , объект регулирования второго порядка
с постоянными времени
, объект регулирования второго порядка
с постоянными времени ![]() и
и ![]() .
.
В таком контуре можно произвести настройку на технический оптимум, если использовать ПИД-регулятор. Передаточная функция неизменяемой части
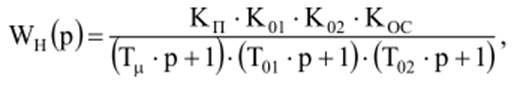
а требуемая передаточная функция регулятора
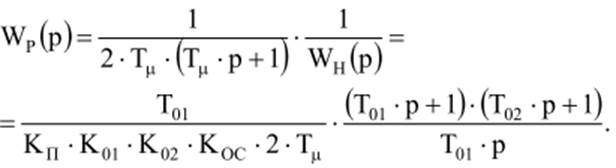
При
этом исключается влияние постоянных времени ![]() и
и ![]() на переходные процессы.
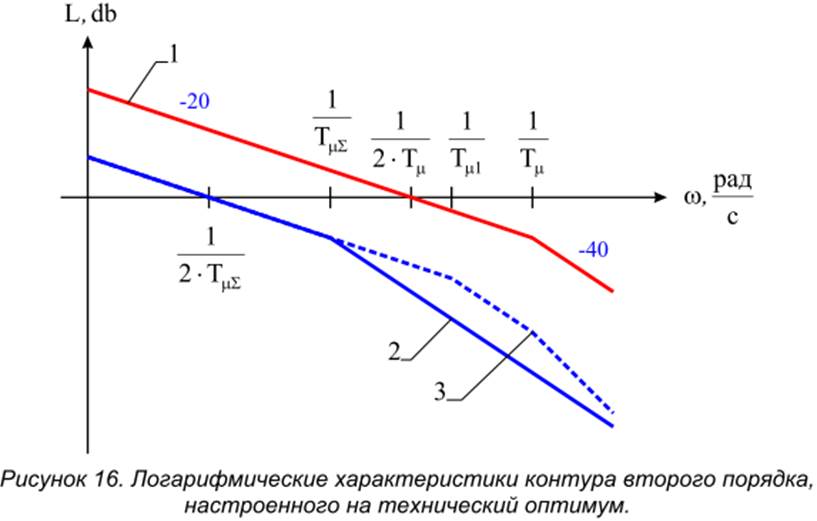
Логарифмическая характеристика контура показана на рис. 16 (кривая 1).
на переходные процессы.
Логарифмическая характеристика контура показана на рис. 16 (кривая 1).
Но, если одна из них, например ![]() незначительна, и нет необходимости
ее компенсировать, то, отнеся ее к малым постоянным времени для
настройки на технический оптимум можно использовать ПИ-регулятор
незначительна, и нет необходимости
ее компенсировать, то, отнеся ее к малым постоянным времени для
настройки на технический оптимум можно использовать ПИ-регулятор
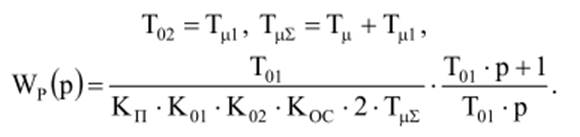
Логарифмическая характеристика контура в этом случае показана на рис. 16 (кривая 2).
Передаточная функция контура, без объединения малых постоянные времени
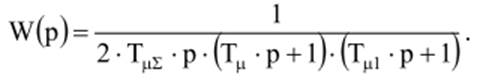
Соответствующая
ей характеристика – кривая 3 на рис. 16. Как видно из характеристик 2 и 3,
снижение расчетного порядка за счет объединения малых постоянных времени
приводит к выбору такого быстродействия, что наибольшая из малых
постоянных времени ![]() дает частоту сопряжения правее
частоты среза более чем на октаву. Т.е. запас устойчивости по фазе в
контуре 3-го порядка не менее, чем в контуре 2-го порядка, настроенном на
технический оптимум.
дает частоту сопряжения правее
частоты среза более чем на октаву. Т.е. запас устойчивости по фазе в
контуре 3-го порядка не менее, чем в контуре 2-го порядка, настроенном на
технический оптимум.
Звенья с малыми постоянными времени располагаются и в каналах обратных связей. При определении эквивалентной постоянной времени для звена в прямом канале регулирования лучше воспользоваться не суммированием, а формулой Д.С. Ямпольского
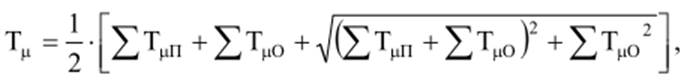
где ![]() - малые постоянные времени звеньев
в прямом канале,
- малые постоянные времени звеньев
в прямом канале,
![]() - малые постоянные времени звеньев
в канале обратной связи.
- малые постоянные времени звеньев
в канале обратной связи.
8. Частотный метод синтеза.
Частотный
метод синтеза - синтез по желаемым логарифмическим характеристикам. Если
передаточная функция неизменяемой части контура ![]() определена по параметрам элементов
(объект регулирования, преобразователь, обратная связь) и определен
коэффициент передачи регулятора
определена по параметрам элементов
(объект регулирования, преобразователь, обратная связь) и определен
коэффициент передачи регулятора ![]() по требуемым статическим
показателям, а желаемая передаточная функция
по требуемым статическим
показателям, а желаемая передаточная функция ![]() контура выбрана с учетом требований
динамики, то регулятор должен обладать передаточной функцией
контура выбрана с учетом требований
динамики, то регулятор должен обладать передаточной функцией
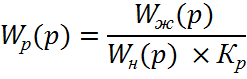
Рассматривая логарифмические характеристики
![]()
Т.о., имея асимптотические характеристики неизменяемой части контура и желаемую, геометрическим вычитанием можно определить асимптотическую характеристику регулятора.
Рассмотрим на примере одноконтурной системы управления скоростью двигателя постоянного тока.
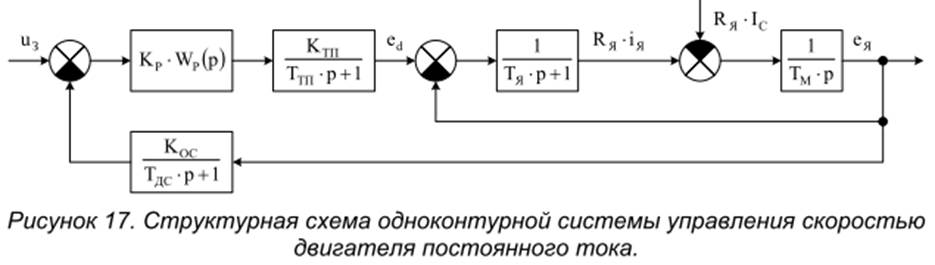
Если основная задача системы – стабилизация скорости, то можно производить синтез по возмущению. Передаточная функция системы по возмущению
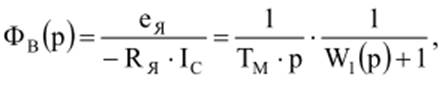
где
![]() - передаточная функция разомкнутого
контура по сигналу
- передаточная функция разомкнутого
контура по сигналу ![]()
Для получения ![]() преобразуем схему, как показано на рис.
18.
преобразуем схему, как показано на рис.
18.
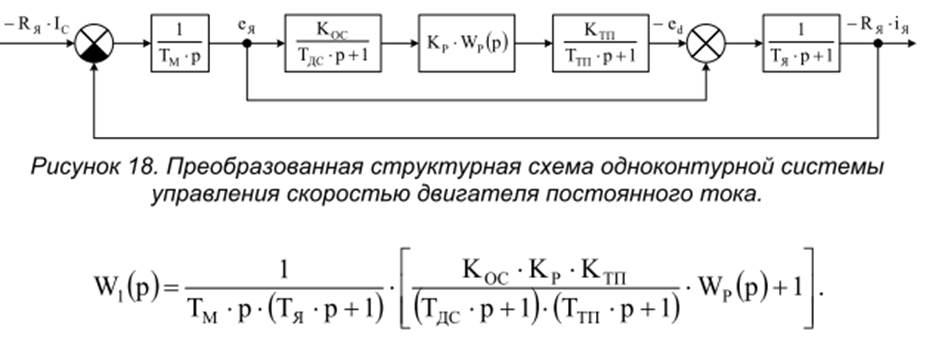
Пренебрегая
внутренней обратной связью двигателя по ЭДС якоря и заменяя два
апериодических звена одним эквивалентным с малой постоянной времени ![]() получим
получим
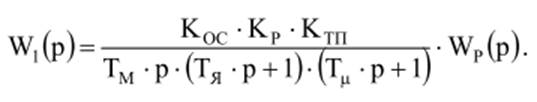
Логарифмическая амплитудная характеристика неизменяемой части системы
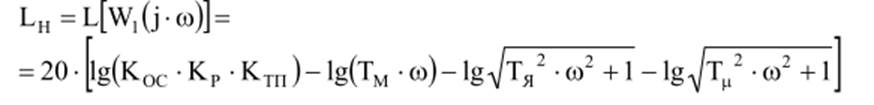
показана на рис. 19.
Если в качестве желаемой взять спрямленную характеристику, то
статические показатели не изменятся, замкнутый контур будет
соответствовать апериодическому звену, но частота среза![]() будет недопустимо большой
будет недопустимо большой ![]() . Это недопустимо из-за низкой
помехоустойчивости и возможном появлении автоколебаний. Обычно для электроприводов
постоянного тока контур скорости имеет частоту среза
. Это недопустимо из-за низкой
помехоустойчивости и возможном появлении автоколебаний. Обычно для электроприводов
постоянного тока контур скорости имеет частоту среза ![]() . Для обеспечения необходимого запаса
устойчивости в среднечастотной области характеристика должна иметь наклон
-20 db/дек . Для обеспечения этого желаемая
характеристика должна иметь две точки излома на частотах
. Для обеспечения необходимого запаса
устойчивости в среднечастотной области характеристика должна иметь наклон
-20 db/дек . Для обеспечения этого желаемая
характеристика должна иметь две точки излома на частотах ![]() и
и ![]() . Желаемая характеристика правее
частоты среза должна иметь изломы там же, где и характеристика
неизменяемой части. Путем геометрического вычитания получим характеристику
регулятора
. Желаемая характеристика правее
частоты среза должна иметь изломы там же, где и характеристика
неизменяемой части. Путем геометрического вычитания получим характеристику
регулятора ![]() , которая соответствует передаточной
функции
, которая соответствует передаточной
функции
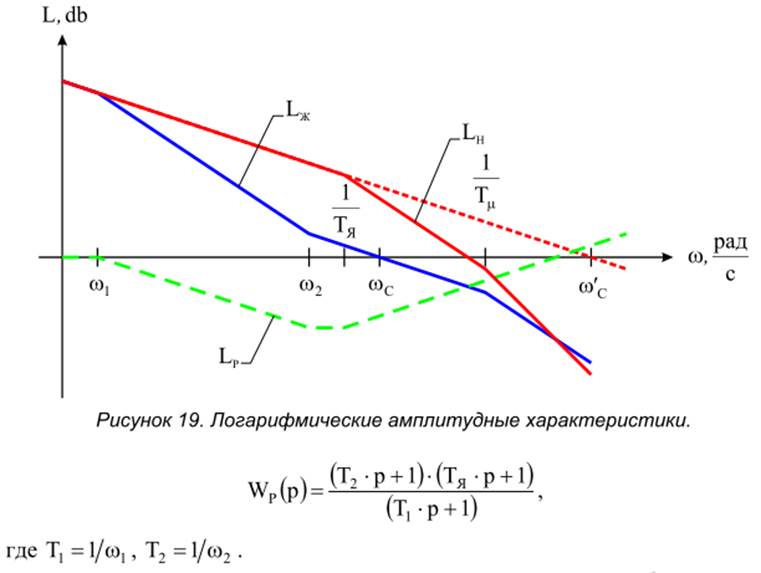
Т.о. основной задачей при частотном синтезе является выбор основных точек желаемой характеристики исходя из требуемого быстродействия, перерегулирования и достаточного запаса устойчивости по фазе или колебательности.
9. Ограничения координат САУ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.