Расчет надежности систем автоматики, страница 2

        В дальнейшем под объектами подразумеваются системы автоматизации производственных процессов, для которых существенно именно время безотказной работы. Введем для него обозначение . В теории надежности для измерения времени принята внесистемная единица – час.

         Как известно из теории вероятностей, исчерпывающей характеристикой случайной величины (в данном случае – ) является ее распределение,  т. е. вероятность того, что  меньше наперед заданного значения времени t. Эта вероятность является функцией t, что подчеркивается другим ее обозначением:

             .                                                          (1)

         В теории надежности вместо  используют эквивалентную ей характеристику − вероятность безотказной работы , определяемую как вероятность того, что   больше заданного значения времени t:

                                               .                                                       (2)

Обе характеристики связаны простым соотношением

                                   .                                                   (3)

Обычно при описании свойств безотказности простых элементов и несложных систем автоматики считают, что зависимость R(t) от времени имеет следующий вид (так называемый экспоненциальный закон надежности):

                                       , t≥ 0.                                                  (4)

        Постоянный  параметр  в этой зависимости называется интенсивностью отказов. Он имеет размерность 1/час. Чем больше , тем меньше вероятность R(t) того, что система будет работать без отказа до момента t, т. е. тем меньше ее надежность.

                   Распространенной характеристикой надежности является среднее время безотказной работы (средняя наработка до отказа), представляющее собой математическое ожидание случайной величины :

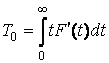                                            .                                                         (5)

Штрихом обозначена производная.

         В случае экспоненциального закона надежности между и существует простая связь

                                                  .                                                                   (6)

         Рассмотренные количественные характеристики или, как их называют иначе, показатели надежности  описывают свойства безотказности системы. Однако в понятие надежности включают и другие ее свойства – такие, как ремонтопригодность, долговечность и сохраняемость. При расчете надежности в курсовом или дипломном проекте достаточно ограничиться учетом свойств безотказности и  ремонтопригодности (приспособленности объекта к предупреждению, обнаружению и устранению отказов). Для количественного описания свойства ремонтопригодности пользуются показателем − средним временем восстановления системы после отказа.