Проблема надёжности измерений. Показатели надёжности невосстанавливаемых систем. Экономическое обоснование надёжности, страница 3

; ; ; ; . Определить объем представительной выборки.

         Решение:

1.  определяем вспомогательный коэффициент :

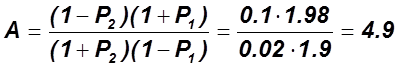
при  , при  .

Выбираем . В этом случае выше риск изготовителя.

2.  По таблице для заданных , , и  определяем .

3.  Составляем план испытаний: , ,  при  и .

2. Для известного закона распределения.

Для экспоненциального закона:

                        

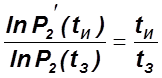
Сокращая время испытаний, мы увеличиваем значение , выбирая его из таблицы П4.

Пример №3:

Дано: , , . Определить объём выборки и составить план контроля.

1.  Задаёмся временем испытаний: , .

2.  Определяем соотношение : ,   .

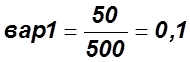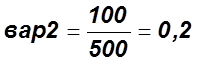3.  Задаёмся .

4.  По таблице для заданного  и  

                              

5.  По таблице П2 для заданных ,  и : ; для : . При : .

6.  План контроля , , , при , .

Для планирования испытаний с учётом интересов потребителя и изготовителя используется вспомогательный коэффициент  (смотри предыдущую задачу).

3.  Решение задачи графическим методом.

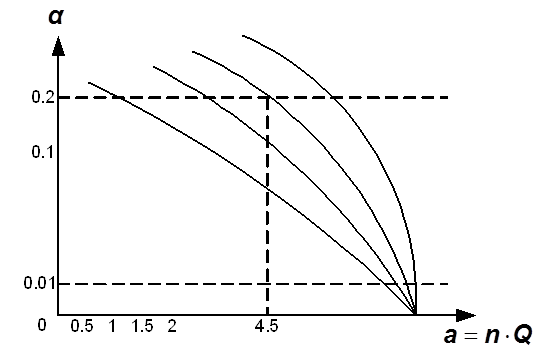                                                                                                     Недостаток:

              погрешность более 5%

    Преимущество:

                        Простота

               

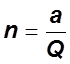
Пример:

, , . Определить .

1.  На пересечении ;  находим ;

2.  Находим .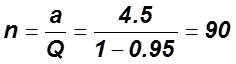

Определение межповерочного интервала.

1.  МПИ определяют для группы однотипных приборов.

2.  МПИ назначают в соответствии с условиями эксплуатации (ГОСТ 8.002).

3.  В процессе эксплуатации приборов МПИ корректируют.

4.  МПИ назначают из следующего ряда6 1, 2, 3, 4, 5…. Лет.

5.  Назначение МПИ устанавливают по разным методикам для рабочих СИ и образцовых СИ.

Исходные данные для определения МПИ.

1.  Значение показателей безотказности и интенсивности отказов.

                        

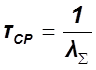
2.  Число поверяемых СИ.

3.  Число СИ, имеющих метрологические отказы - .

4.  Число Си, имеющие явные отказы.

5.  Суммарная погрешность СИ - .

6.  Допуск на контролируемые параметры - .

7.  Периодичность контроля - .

8.  Среднее время восстановления - .

9.  Коэффициент использования - .

10. Коэффициент метрологических отказов - .

Методика определения МПИ.

1.  Определение МПИ 

 - средняя наработка на метрологический отказ.

2. 

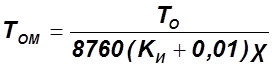
3. 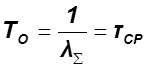  - средняя наработка на отказ.

4.   - требуемая вероятность метрологического отказа.

Пример: определение МПИ.

1.  Определяем       

2. 

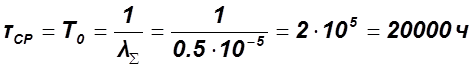
3. 

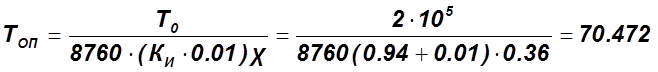
4. 

Значения коэффициентов  и .

СИ	Подгруппа
Радиотехнические	Г – генераторы Ф – фазометры Д – аттенюаторы В – вольтметры М – измерение мощности Ч – измерение частоты и времени И – импульсное напряжение У – усилители измерительные Б – источники питания Я – блоки измерительные	0,4 0,2 0,21 0,36 0,3 0,4 0,17 0,14 0,17 0,17	0,023 0,017 0,043 0,94 0,051 0,051 0,033 0,017 0,023 0,023
Электрические	щитовые переносные	0,22 0,39	0,21 0,081
Тепловые и механические	давления расхода температуры	0,27 0,25 0,23	0,49 0,34 0,28

Определение методики достоверности

,

где  - методическая погрешность;

          - инструментальная погрешность;

- погрешность оператора.

1) 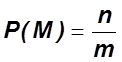,  - количество проверяемых параметров;

                  - общие параметры, необходимые для проверки.

2) ,  - вероятность забракования годного прибора;

 - вероятность признания годным, бракованного прибора.                       

3)  - выбираем из ряда (0,9; 0,95; 0,97; 0,99)        .

Определение  и  при независимых параметрах

прибора

;

.

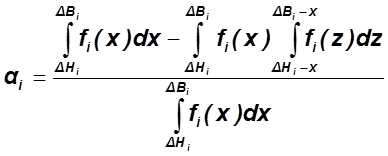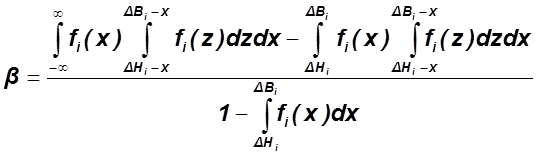Таблица значений  и

	Вероятность ложного отказа		Вероятность необнаруженных отказов
	-нормального распр - ния	- равномерного распр - ния	-нормального распр - ния	- равномерного распр - ния
0,1	0,006	0,012	0,004	0,011
0,2	0,013	0,026	0,011	0,021
0,3	0,02	0,039	0,015	0,032
0,4	0,028	0,052	0,021	0,04
0,5	0,035	0,066	0,026	0,049
0,6	0,044	0,079	0,031	0,056
0,7	0,053	0,093	0,036	0,063
0,8	0,061	0,106	0,041	0,07
0,9	0,071	0,12	0,046	0,076
1,0	0,081	0,13	0,05	0,082

Практическая методика

1)  Определяем  ;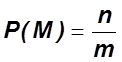

2)  Определяем ;

2.1) по таблице находим ;

2.2) по таблице находим  и  (нормальный закон);

3) Определяем  - выбираем из ряда (0,9; 0,95; 0,97; 0,99) .

4) .

Основные законы наработки до отказа.

1)  Экспоненциальное;

2)  Нормальное;

3)  Вейбулла – Гнеденко;

4)  Равномерное;

5)  Рэллея;

6)  Гамма;

7)  Эрланга.

Экспоненциальное распределение.

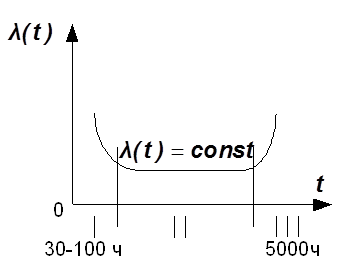
Экспоненциальное распределение нашло широкое применение в сложных измерительных системах.

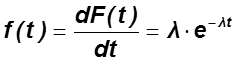
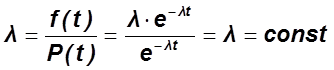
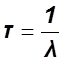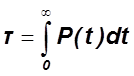,  - для непрерывной величины;

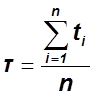 - для дискретной величины.

                           

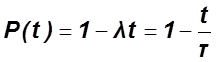
Погрешность формулы составляет

         Экспоненциальное распределение используется для определения безотказной работы  на интервале . Оно применяется в сложных системах без учёта этапа износа и старения. Основное преимущество этого распределения – простота математических выражений.

, ,

Нормальное распределение.