Проблема надёжности измерений. Показатели надёжности невосстанавливаемых систем. Экономическое обоснование надёжности, страница 2

3) ;

4) ;

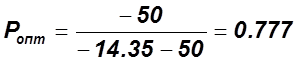5) .

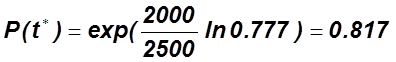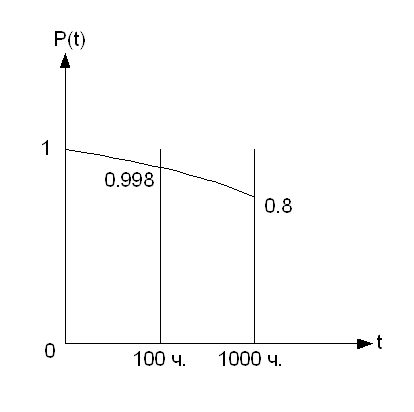
Локальные системы (В-2)

         Прибыль от использования системы известна. Система работает в масштабе реального времени. Оптимальный уровень надежности определяется из условия максимума экономического эффекта.

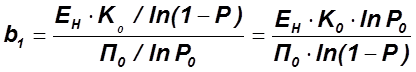
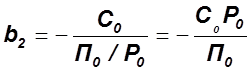
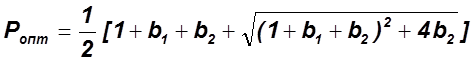
Пример 2:

Исходные данные: условие примера 1, известна прибыль

1) ;

2) ;

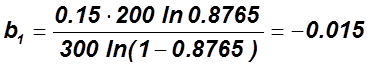3) ;

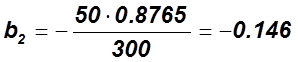4) ;

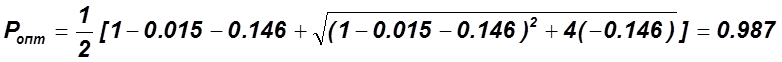5) .

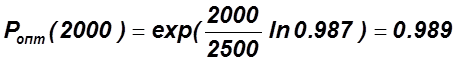Интегрированные многоуровневые системы.

Система работает в масштабе реального времени и при появлении отказов даёт ущерб. Оптимальный уровень надёжности определяется из условия минимума суммы и приведённых затрат на проектирование, изготовление, эксплуатацию.

;             

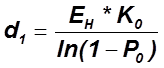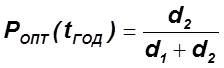
Пример 3:

Условие задачи №1, известен ущерб

1)  ;

2)  ;

3)  ;

4)  ;

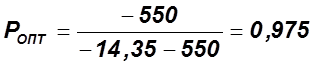5) 

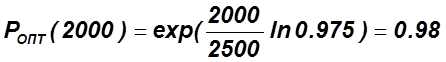
Пример 4:

Условие задачи №1, известен ущерб

1)  ;

2)  ;

3)  .

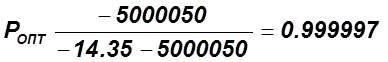Метод расчёта сверху вниз.

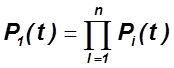
Если приборы равнонадёжные, то:

                                

          - интенсивность работы;

           - время отказов;

                    

Зная количество типовых модулей в приборах

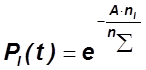
Пример:

Задана вероятность безотказной работы .  В системе имеется 3 прибор, которые содержат следующее количество элементов:

                                                  

1) 

2) 

3) 

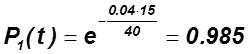
4) 

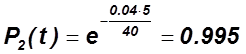
5) 

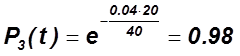
6) 

Классические методы расчёта простейших структур

последовательное

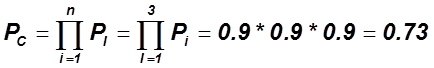
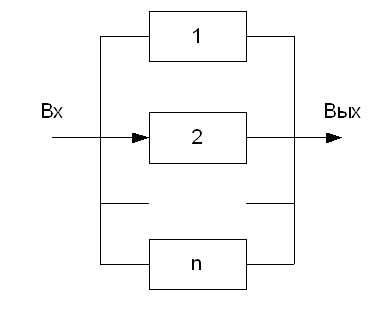                                                                                                  Параллельное

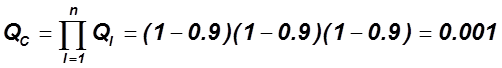
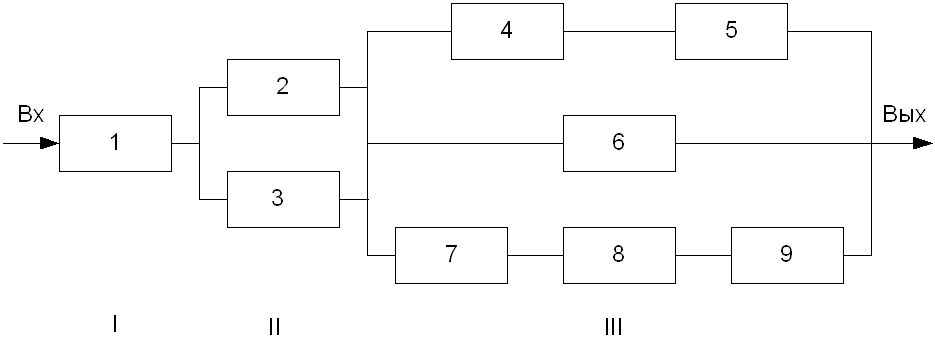
Смешенное

Сложную схему разбиваем на участки удобные для расчета известными нам методами

                        

                                            ;          ;

                                            ;  ;

                                                                        ;

                                                                         .

Экспоненциальный закон.

Расчет надежности системы

при последовательном соединении.

       

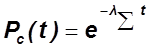
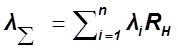
Нужно выбирать . Этот метод называется снизу вверх.

Расчет надежности более сложных структур.

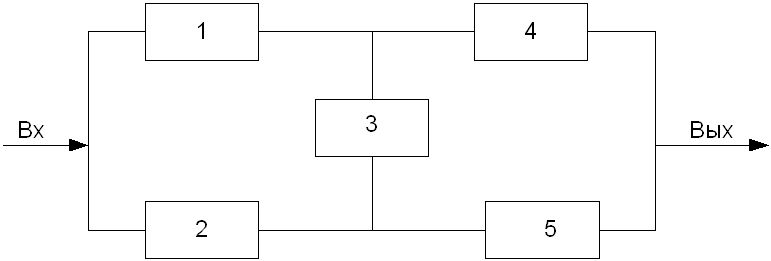
Метод перебора состояний

Если система не резервирована, то расчет ведется на один отказ.

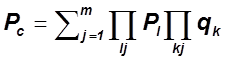
№ состояния	1	2	3	4	5	Вероятность состояния
1	+	+	+	+	+
2	-	+	+	+	+
3	+	-	+	+	+
4	+	+	-	+	+
5	+	+	+	-	+
6	+	+	+	+	-
7	-	-	+	+	+
8	-	+	-	+	+
9	-	+	+	-	+
10	-	+	+	+	-
11	+	-	-	+	+
12	+	-	+	-	+
13	+	-	+	+	-
14	+	+	-	-	+
15	+	+	-	+	-
16	+	+	+	-	-

Метод позволяет рассчитывать любые структуры. Недостаток: большая трудоёмкость. При большом количестве элементов в системе составляют программу.

         Варианты структур, которые можно рассчитывать по этому методу.

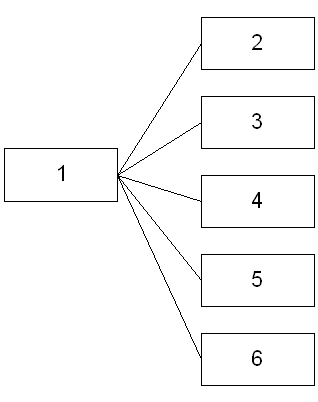Мостиковая

    При отказе первого элемента схема не работает.

Радиальная

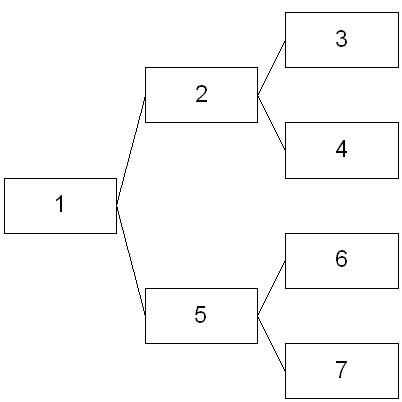
Древовидная

Если отказывает второй и четвертый, то третий блокируется

Кольцевая

   

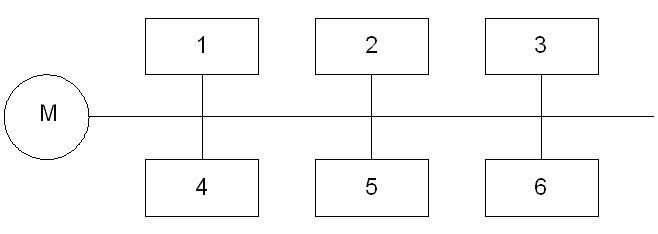
Магистральная

Метод разложения относительно особого

элемента

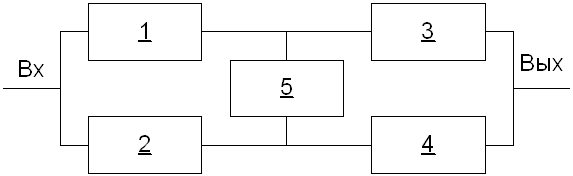
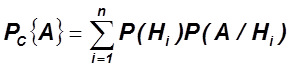
1)

 

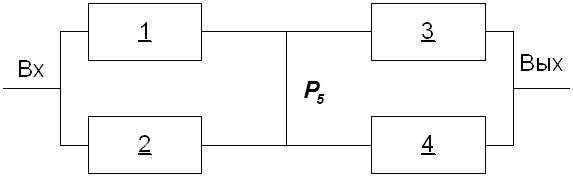
2)

                                                                                                          

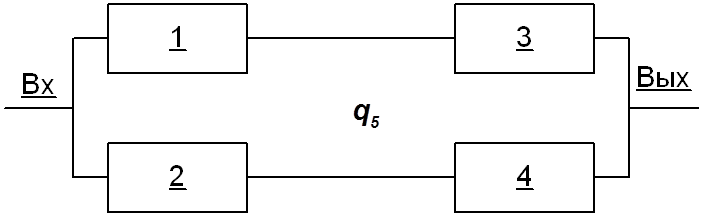
Метод минимальных путей и сечений

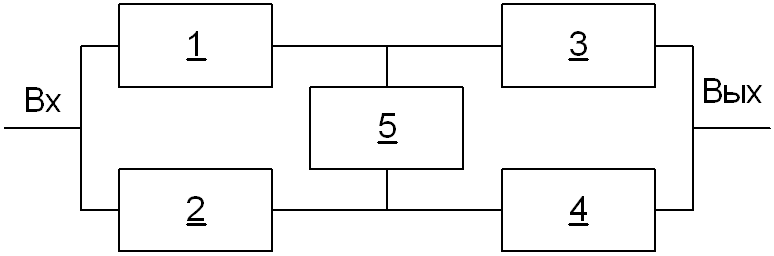
путей

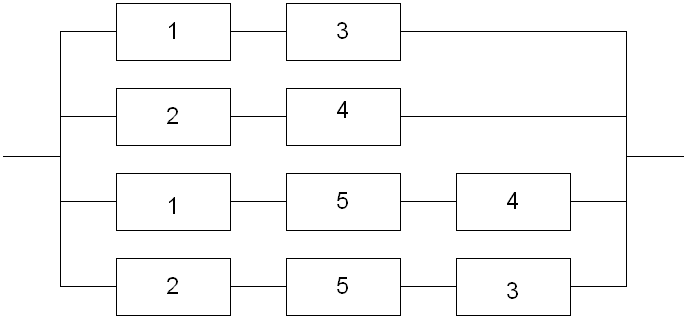
сечений

Логико-вероятностный метод

         Этот метод основан на математической логике и использует следующие законы:

1)  Тождества;

2)  Коммутативности;

3)  Ассоциативности;

4)  Дистрибутивности;

5)  Дуализма;

6)  Поглощения.

Метод однократной выборки

         Позволяет решить вопрос о приеме партии изделий на основании результатов испытаний представительной выборки случайно отобранной из общей партии изделий.

 - объем партии, .

 - объем представительной выборки, . ()

 - приёмное число отказов в представительной выборке ()

 - время испытаний ()

                                         - число фактически отказавших

                        Метод однократной выборки                     проводят как для известного закона распределения контролируемого параметра, так и для неизвестного.

1. Для известного закона распределения

         В этом случае используются два закона распределения: либо биномиальный, либо Пуассона.

Закон Пуассона: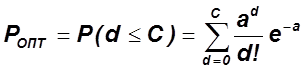              

  - количество приборов в выборке

 - вероятность отказов.

Пример №1:

         Задана вероятность безотказной выборки , ,  - интерес потребителя. Определить   и .

         Решение:

1.  Определяем , .

2.  По таблицам приложениям П2: для вероятности ; : ; для ; ; ; для ; ; .

Решение задачи, учитывающей интересы изготовителя () и потребителя ().

Если , то .

Риск заказчи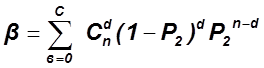ка:                         

- Вероятность для заказчика ().

 - Количество фактических отказов.

 - Количество допустимых отказов.

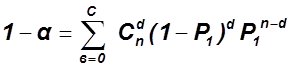
 - Риск изготовителя ().

Задача решается с помощью коэффициента :

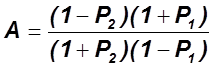
Пример №2: