Проблема надёжности измерений. Показатели надёжности невосстанавливаемых систем. Экономическое обоснование надёжности, страница 13

4.  системно – независимым аргументом;

5.  графовые модели.

Эмпирические модели

Эмпирические модели – основаны на анализе накопленной информации о функциональной зависимости программных протоколов ранее разработанных. На 1000 операторов 10 ошибок.

,

 - число операторов или  - программ.

1.1.  Модель Хостеда оценивает количество ошибок в программе после окончания её разработки:

 - коэффициент пропорциональности.

, - число операторов и операндов.

1.2.  Модель IBM.

 - число модулей ПО, потребовавших более 10 исправлений.

 - число модулей ПО, потребовавших менее 10 исправлений

1.3.  Модель, учитывающая число дефектов в программе в зависимости от объёма и сложности.

СОМР – сложность программы, определяющаяся функциями и количеством внутренних и внешних связей.

 - число операторов.

Недостатки эмпирических  моделей.

1.  Дают грубую приближённую оценку надёжности ПС, на этапе технических предложений позволяют выбрать наиболее рациональный вариант.

2.  Оперируют только с понятием корректности ПС, определяются числом программных ошибок.

3.  Не отражают динамики вычислительного процесса при эксплуатации программных средств.

Статистические модели

         Связаны с числом ошибок, которое определяется простыми статистическими методами (на основании интуитивных допущений). Эти модели не учитывают закон распределения случайных чисел.

2.1. Модель Миллса.

         Метод предполагает внесение некоторого известного количества ошибок в различные места программ. Далее разрабатывается контрольный тест, выявляющий искусственно внесённые ошибки и неизвестные.

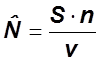
 - число искусственных ошибок, внесенных в программу.

 - число искусственных ошибок, выявленных в результате тестирования.

 - число ошибок, выявленных тестом и неизвестных нам.

 - статическая мера доверия, определяющая количество ошибок

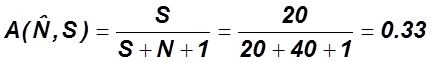
2.2. Модель Коркорэна

         Предполагает наличие в программе многих источников отказов, связанных с различными типами ошибок и разной вероятностью их проявления. Аргументом модели является число проколов программы .

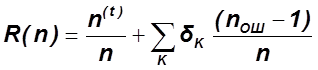 - вероятность безотказного функционирования.

 - число успешных прогонов.

 - число обнаруженных ошибок К-ого типа с вероятностью .

 

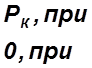
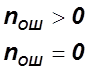
2.3. Модель параллельного тестирования.

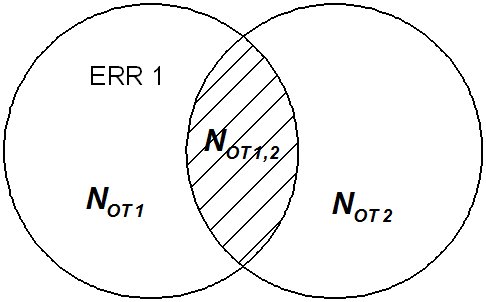
         Метод предусматривает участие 2-ух групп независимых программистов, каждая из которых использует свою стратегию поиска ошибок. Предполагается, что множество ошибок выявляется 1-м и 2-м тестом.

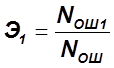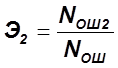; - эффективность тестов 1 и 2.

;       ;        .

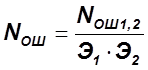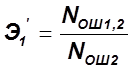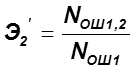Основные характеристики статистических моделей

1.  Статистические модели отражают подход к понятию надежности программных средств как единичные характеристики, оценивающие ее корректность.

2.  Основной параметр – число ошибок в программе.

3.  По применимости статистические модели относят к оценочным.

4.  Основная область использования статистических моделей – завершающая стадия разработки (эскизное проектирование, техническое и ОКР).

5.  Статистические модели могут ограничиваться на стадии фондирования.

Вероятностные модели

         Максимальная представительная группа, к которой относят наиболее сложные модели, описывающие случайный процесс обнаружения и проявления программных дефектов и отказов.

3.1. Модель Джелин - Моранды

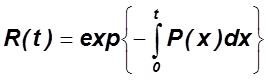 - вероятность безотказной А программ в интервале от 0 до .

,

 - число ошибок, обнаруженных за время ;

 - начальное количество ошибок;

 - коэффициент пропорциональности.

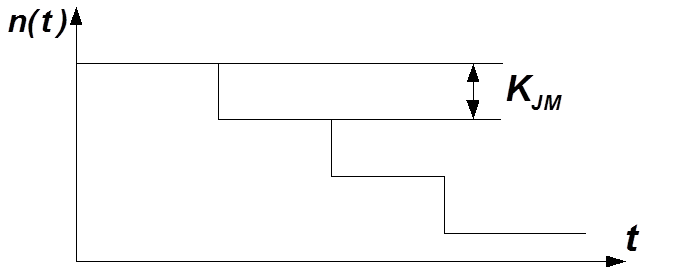
Модель не учитывает внесение новых ошибок в процессе исправления обнаруженных.

3.2. Модель Муссы

         В качестве аргумента показателей надежности выбрано определенное время  отладки и операционное время  функционирования программ в составе выполненной системы.

,

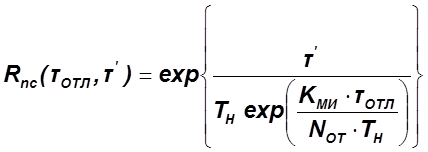 - время отладки;

 - время функционирования;

 - начальное время наработки программы на отказ;

 - коэффициент модели, учитывающий уплотнение тестового времени по сравнению со временем эксплуатации.

Вероятностные модели исследует надежность как единичное свойство программ, характерно только их корректность. По мере усложнения моделей число параметров увеличивается. По классификации применяемости вероятностные модели относятся к классу оценочных, они имеют ограниченное применение на завершающих стадиях жизненного цикла программных средств.

Основные причины ограниченного применения

1.  Поток программных отказов при приемосдаточных испытаниях характерен малой интенсивностью, чтобы выявить фактическое число ошибок в программе необходимо большое время и материальные затраты;

2.  На стадии сопровождения не все выявленные программы: ошибки подлежат устранению. Чаще всего вводят дополнительное ограничение на область входных данных имеющих возможность возникновения отказа;

3.  Статистический анализ данных о программных ошибках по представительным набором разных независимых проектов показал, что эти данные не могут быть описаны каким – либо общим законом распределения, так как причинами являются: влияние человеческого фактора, влияние операционной среды, влияние условий эксплуатации.

Модели с системно – независимых аргументам

Модель Нельсона

         В основе предположения, что специфицированная область значений векторов выдаваемых данных состоит из двух подмножеств:

1.  - наборы данных, не вызывающие отказов;

2.  - наборы данных, вызывающие отказы программ.

Тогда  вероятность отказа ,

 - случайный набор входных данных , который вызывает отказы программного обеспечения.

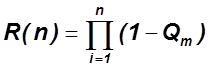 или .

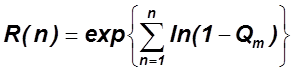Модель Нельсона – это одно параметрическая вероятностная модель с линейно – независимым аргументом. Практическое использование модели Нельсона вызывает трудности в связи со сложностью нахождения распределения вероятности.

         Для устранения этих недостатков используются структурные графовые модели.