Основные технические характеристики ЦИП и АЦП, страница 5

Таким образом, расхождение между qN_i и x(t_i) характеризует точность результатов преобразования. Для более детального выявления причин этого расхождения на рис.1.20,б в более крупном плане показан небольшой участок x(t). Здесь дополнительно учтены обстоятельства, которые было бы трудно показать на рис 1.20, а:

1)номинальные значения дискретных уровней q_номN_i отличаются от их действительных значений qN_i(горизонтальные штрихпунктирные линии);

2) действительные моменты времени начала циклов преобразования (вертикальные штрихпунктирные линии) отличаются от их номинальных значений ; если, например, команда начала цикла синхронизирована сетевым напряжением, то нестабильность его частоты будет создавать эти отличия.

Расхождение между полученным результатом !!!(темная точка) и истинным мгновенным значением !!!(крестик), которое можно назвать абсолютной погрешностью цифрового измерения этого мгновенного значения !!!!, содержит несколько составляющих, обусловленных разными причинами:

– из-за того, что процесс преобразования требует определенного времени ;

 – из-за того, что моменты времени t_i, к которым относятся числа N_i, отличаются от моментов, когда в действительности начинаются очередные циклы преобразования;

– из-за того, что численный результат измерения N_i соответствует номинальным значениям дискретных уровней, которые отличаются от действительных значений;

– из-за самой дискретности этих уровней.

Перечисленные составляющие можно разделить на две группы:

1) и  зависят не только от свойств прибора, но и от поведения во время исследуемого процесса; при большей скорости изменения x(t) они увеличиваются [см. соседний (i+1)-й цикл], если x(t)=const(статика), они исчезают, эти составляющие можно назвать динамическими погрешностями;

2)  и  остаются и при x(t)=const; их можно в этом смысле назвать статическими погрешностями;

Надежность

Вопросы надежности рассматриваются в специальной технической литературе и соответствующих курсах (см., например, !50!). Здесь остановимся только на определении основных показателей, характеризующих надежность ЦИУ.

Надежность – это свойство относящееся к любым техническим объектам, в частности к средствам измерений.

Надежность – это сложное свойство включающее свойства безотказности, долговечности, ремонтопригодности и сохраняемости. Эти понятия в иерархической системе стоят «под » надежностью. Их количественные характеристики – это показатели надежности. Все эти понятия основаны на изучении явлений отказа, т.е. нарушения работоспособности объекта. Отказ – это случайное событие, а интервал времени от начала эксплуатации работоспособного объекта(t=0) до отказа (t=T) – непрерывная случайная величина с областью возможных значений 0<T<. Функция распределения случайной величины T выражает вероятность того, что в течении времени t произойдет отказ Q(t)=Bep(T<t), где ВерА – вероятность события А, а функция P(t)=1-Q(t)=Bep(t<T)- вероятность того, что за время t отказа не будет, т.е. вероятность безотказной работы. Функция Q(t) является неубывающей, а P(t) – невозрастающей, причем Q(0)=P()=1 и Q()=P(0)=1. Для количественной характеристики надежности применяют разные числовые характеристики функции распределения Q(t).

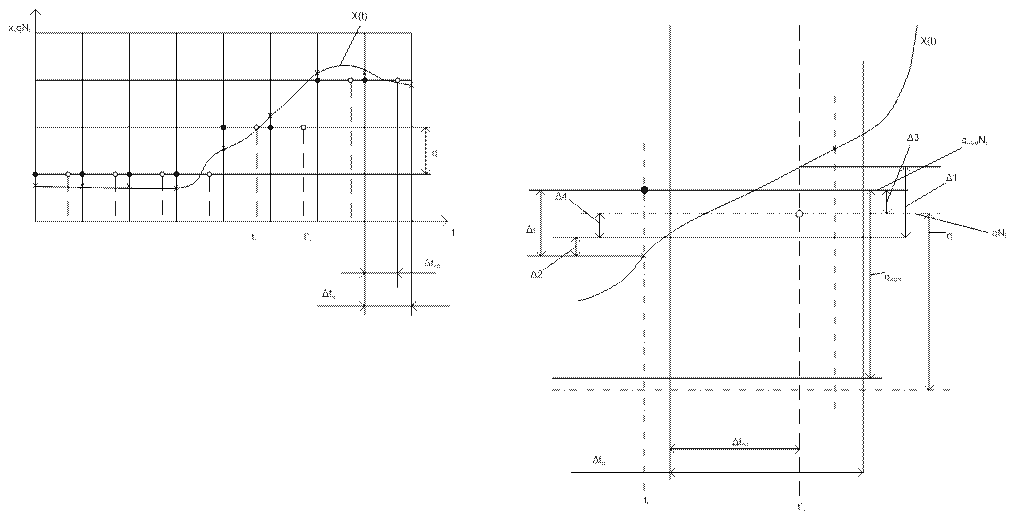Рис. 1.20

Согласно стандарту [16] основным показателем надежности для любых средств измерения устанавливается так называемая наработка на отказ. Применительно к ним под «наработкой » понимают продолжительность работы объекта, а под «наработкой на отказ» (обозначим T₀) – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течении этой наработки [46]. Это – вероятностное определение понятия T₀. Согласно [16] значение T₀ в новых разработках должно быть не менее 1000ч.

Нормирование показателей надежности сопряжено, разумеется, с их экспериментальной проверкой, т.е. с испытаниями на надежность. Испытания состоят в накоплении статистических данных об отказах в течение длительного времени на многих экземплярах. И все же ограниченность времени испытаний и ограниченность выборки, т.е. количества испытуемых объектов, приводят к тому, что получаемые статистические значения показателей надежности отличаются от вероятностных значений, представляют их приближенные оценки. Статистическая оценка «наработки на отказ» может быть вычислена по результатам испытаний следующим образом:

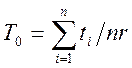
где n- число испытываемых объектов; r – число отказов за время испытаний; t_i – наработка i-го объекта до отказа.

Согласно стандарту [44] для ЦИУ, измеряющих (преобразующих) напряжения токи и сопротивления, в качестве показателя безотказности в соответствии с требованием стандарта [16] установлена наработка на отказ, причем значение Т₀ должно быть не менее 1500 ч для ЦИП и 2000ч для АЦП. Показателями долговечности стандарт [44] устанавливает либо средний срок службы, либо средний ресурс, либо так называемый гамма-процентный ресурс. Срок службы и ресурс – это соответственно календарная продолжительность эксплуатация объекта и его наработка от ее начала или возобновления после среднего или капитального ремонта до наступления такого предельного состояния, при котором дальнейшая эксплуатация должна быть прекращена по тем или иным причинам. Средний срок службы и средний ресурс в вероятностном смысле являются математическими ожиданиями этих показателей, а при испытаниях их статистические оценки определяются как средние арифметические значения для испытуемой выборки.

Гамма – процентный ресурс – это наработка, в течении которой объект не достигнет предельного состояния с заданной вероятностью , %.

Согласно стандарту [44] значение среднего срока службы ЦИУ до списания должно быть не менее 8 лет, а значение ресурса (среднего или гамма- процентного при =0,90; 0,95; 0,98) должно выбираться из ряда 2000; 3000; 5000; 8000; 16000; 25000; 50000ч.

В качестве показателя ремонтопригодности стандарт [44] устанавливает среднее время восстановления. В вероятностном смысле – это математическое ожидание времени восстановления работоспособности.

При наличии статистических данных о длительностях восстановления ряда объектов (включая время поиска причины отказа) оценка среднего времени восстановления вычисляется как среднее арифметическое длительностей в данной выборке. Согласно [44] среднее время восстановления должно выбираться из ряда 1; 1,5; 2; 4; 6; 10; 12; 18; 24; 36; 48; 96ч.