Основные технические характеристики ЦИП и АЦП, страница 4

за 24 ч при 231⁰С, относительной влажности не более 50 %;

за 3 мес при 205⁰С, относительной влажности не более 95%;

за год при 10-35⁰С, относительной влажности не более 95%.

ТАБЛИЦА

Uном, B	c/d

Для моделей высокой точности помимо этого могут быть указаны в отдельности временная и температурная нестабильность, например  (0,002% of R+0,001% of FS) за 24 ч; (0,01% of R+0,02% of FS) за 3 мес при    1⁰С; относительной влажности не более 50%; (0,0002% of R+0,0001% of FS) на 1⁰С в диапазоне 0-50⁰С.

В последние годы в СССР в соответствии с идеями, нашедшими отражение в [15], при нормировании точности все больше учитывается тот факт, что общая погрешность  является случайной величиной, поскольку она может быть представлена в виде суммы

,

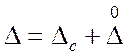Поэтому в [16 u 44] предусматриваются два варианта нормирования основной погрешности любых средств измерения:

а) в виде предела допускаемой общей погрешности, например ;

б) в виде отдельных пределов для систематической составляющей, например  и среднего квадратического отклонения случайной составляющей, например .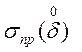

Быстродействие

Обычно быстродействие ЦИП и АЦП характеризуется временем одного преобразования входной величины в код или частотой повторения таких преобразований.

Примеры.1. Цифровой вольтметр совершает одно преобразование измеряемого напряжения в код за 20 мес, т. е. частота повторения таких преобразований составляет 50 преобр./с.

2. Цифровой вольтметр высокой точности совершает одно преобразование за 1 с.

3. В цифровой частотомере время одного преобразования измеряемой частоты в код, т.е. время счета, может быть установлено по выбору 0,1; 1,0; 10с.

4. В АЦП время одного преобразования напряжения в двоичный код составляет 50 мкс, т.е. частота повторения преобразований 2!10⁴ преобр./с (существуют АЦП, у которых частота повторения 10⁶ преобр./с и более).

Смысл этой характеристики, в частности, состоит в том, что по ней можно ориентировочно определить, пригоден ли данный ЦИП или АЦП для получения информации о меняющейся во времени величине x(t)=var. Например, может быть поставлено такое условие: за время одного преобразования изменения x(t) не должно превышать одного кванта q:

.

При таком условии ЦИП или АЦП с данными значениями q и  пригоден для исследования процессов x(t), скорость которых dx/dt не превышает значения .

Это, конечно, не значит, что человек, наблюдающий показания ЦИП, может составить себе представление о процессе, меняющемся с такой скоростью. Человек не сможет даже прочитать многоразрядные числа, меняющиеся со скоростью, например, 50 чисел/с. Предполагается, что информация о процессе не непосредственно воспринимается человеком, а поступает либо в память ЭВМ, либо на быстродействующее регистрирующее устройство и т.п. А для непосредственного восприятия человеком в ЦИП предусматривается устройство, обеспечивающее сравнительно длительную выдержку (экспозицию)  цифрового показания на отсчетном устройстве. Обычно  можно плавно регулировать специальной рукояткой, например, в пределах от 1 до 5с.

В более общем смысле показатели быстродействия связаны с динамическими погрешностями получаемых цифровых результатов измерения.

Рассмотрим этот вопрос.

Положим, что при работе в циклическом режиме временная последовательность кодовых слов каким-нибудь способом зарегистрирована, например напечатана в виде колонки цифр на бумажной ленте. Что можно при этом сказать о точности полученных результатов? Какой смысл имеет само это понятие? Для ответа на этот вопрос нужно прежде всего выяснить, что будем считать окончательным результатом.  Нужно знать, для чего получена последовательность зарегистрированных чисел N₁,N₂,…,N_m, как она будет далее использоваться. Пусть, например, конечная цель состоит в том, чтобы найти среднее значение преобразованного непрерывного процесса за промежуток времени

,

где - длительность одного цикла преобразования.

В этом случае окончательным результатом следует считать среднее арифметическое полученных чисел

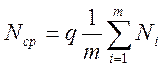
При этом величина абсолютной погрешности

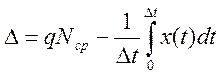                                              (1.16)

характеризует точность результата

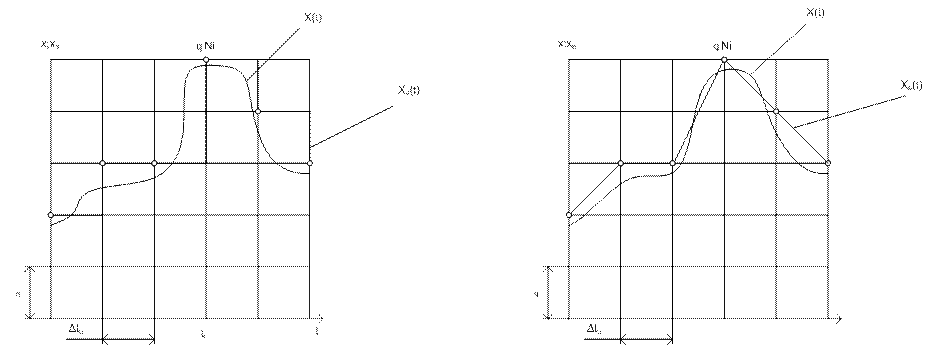Рис. 1.19

Рассмотрим другой пример. Последовательность чисел N₁,N₂,…,N_m  зарегистрирована для того, чтобы по ней «восстановить» исходный процесс x(t). Каждое число N_i «приписывается» к определенному моменту времени t_i, обычно к началу или к концу данного цикла преобразования. По полученным точкам N_i(t_i) можно построить аппроксимацию x_a(t) исходного процесса x(t). Обычно применяют простейшие аппроксимации – ступенчатую(рис. 1.19,а) или кусочно-линейную(рис. 1.19, б). В этом случае определить точность результата – это значит определить степень близости x_a(t) к x(t) по какому-либо критерию. Часто берут критерий максимального отклонения, в котором мерой близости служит величина

.

На рис. 1.19 видно, что кусочно-линейная аппроксимация при прочих равных условиях дает лучшее приближение.

Если важна некоторая общая, интегральная близость x_a(t) к x(t) на участке времени , а отдельные кратковременные всплески типа рис. 1.8,в не имеют существенного значения при исследовании x(t), то применяют интегральный критерий

,                                             (1.18)

А также критерий среднего квадратического отклонения

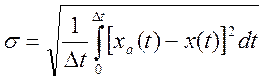
Следует отметить, что формулы (1.16)-(1.19) определяют понятие «точность результата» для рассмотренных случаев, но не дают возможности оценить её количественно, ибо истинная функция x(t) неизвестна (иначе её незачем было бы исследовать). Однако на основании предыдущего опыта могут быть известны некоторые ориентировочные или статистические априорные сведения об x(t). Тогда разумно выбранное определение понятия точности результата может помочь решить ряд практических вопросов.

Во многих случаях заранее неизвестно, какие операции будут производиться с последовательностью зарегистрированных чисел. Тогда окончательным результатом следует считать эту последовательность N_i(t_i), а в понятие «точность результата» вкладывать расхождение между получаемыми мгновенными значениями qN_i(t_i) и истинными мгновенными значениями исходного процесса x(t_i) в эти же моменты времени. Рассмотрим эти расхождения. Будем для определенности считать, что числа N_i приписываются к началу каждого данного цикла. На рис. 1.20, а вертикальные пунктирные линии соответствуют моментам времени t’_i, когда заканчивается процесс преобразования в каждом данном цикле. Светлыми кружками обозначены значения qN_i, полученные в эти моменты времени и соответствующие числовым результатам N_i. Темные кружки отражают то обстоятельство, что значения qN_i, фактически полученные в моменты времени t’_i, приписаны моментам времени t_i, т.е. к началу каждого цикла. Крестиками отмечены мгновенные значения x(t_i).