Рассмотрим сначала погрешность дискретности. Возьмем
времяимпульсный цифровой вольтметр (ВИ ЦВ) и будем считать, что преобразователь
U_ в ![]() и Gидеален. Формула (1.5) была
написана при допущении, что погрешности отсутствуют, в том числе и погрешность
дискретности. Обратим внимание на два обстоятельства: а) сигналы 1 и
2 (рис. 1.3,6) несинхронизированы, т. е. их взаиморасположение во
времени произвольно; б) сигнал 1 неизменен, а длительность импульса в
сигнале 2 может принимать бесчисленное множество значений — это
непрерывная величина (Н). На рис. 1.11,а показано наихудшее в некотором смысле
взаиморасположение сигналов 1 и 2 и соотношение между
и Gидеален. Формула (1.5) была
написана при допущении, что погрешности отсутствуют, в том числе и погрешность
дискретности. Обратим внимание на два обстоятельства: а) сигналы 1 и
2 (рис. 1.3,6) несинхронизированы, т. е. их взаиморасположение во
времени произвольно; б) сигнал 1 неизменен, а длительность импульса в
сигнале 2 может принимать бесчисленное множество значений — это
непрерывная величина (Н). На рис. 1.11,а показано наихудшее в некотором смысле
взаиморасположение сигналов 1 и 2 и соотношение между ![]() и То (
и То (![]() равно целому количеству периодов Т0).
Действительно, в этой ситуации малейшие смещения сигнала 2 и малейшие
изменения
равно целому количеству периодов Т0).
Действительно, в этой ситуации малейшие смещения сигнала 2 и малейшие
изменения ![]() могут давать три
результата: N— 1; N; N+1. Поскольку само значение
могут давать три
результата: N— 1; N; N+1. Поскольку само значение ![]() , а значит, и U_ практически неизменны, это
означает, что может возникать абсолютная погрешности ±q. При любом другом
взаиморасположении сигналов 1 и 2 при любом соотношении между
, а значит, и U_ практически неизменны, это
означает, что может возникать абсолютная погрешности ±q. При любом другом
взаиморасположении сигналов 1 и 2 при любом соотношении между ![]() и Т0 эта
погрешность будет меньше. Но это ещё не погрешность дискретности. Здесь
действуют два упомянутых выше фактора: во-первых, асинхронность сигналов 1и
2; во-вторых, округление непрерывной величины
и Т0 эта
погрешность будет меньше. Но это ещё не погрешность дискретности. Здесь
действуют два упомянутых выше фактора: во-первых, асинхронность сигналов 1и
2; во-вторых, округление непрерывной величины ![]() до ближайшего уровня
дискретной величины NT0.
до ближайшего уровня
дискретной величины NT0.
Первый фактор обусловлен некоторым
несовершенством структуры преобразования ![]() в код, и его можно
устранить, усовершенствовав эту структуру (рис. 1.11,б). Здесь начала
импульса Пуск переходом
в код, и его можно
устранить, усовершенствовав эту структуру (рис. 1.11,б). Здесь начала
импульса Пуск переходом ![]() сигнала 1(рис.
1.11,в), а на счетчик импульсов воздействуют переходы
сигнала 1(рис.
1.11,в), а на счетчик импульсов воздействуют переходы ![]() . Этим достигается не только
синхронизация, но и такое взаиморасположение сигналов 1 и 2, при котором
остается только второй фактор – округление
. Этим достигается не только
синхронизация, но и такое взаиморасположение сигналов 1 и 2, при котором
остается только второй фактор – округление ![]() до ближайшего уровня NT0
, что обуславливает абсолютную погрешность, не выходящую за пределы
до ближайшего уровня NT0
, что обуславливает абсолютную погрешность, не выходящую за пределы ![]() Это – в чистом виде погрешность
дискретности. На рис 1.11,г показана зависимость результата измерения Nqот значения измеряемой
величины U_ рассматриваемого ВИ Ц при отсутствии всех инструментальных
погрешностей, а также зависимость абсолютной погрешности дискретности
Это – в чистом виде погрешность
дискретности. На рис 1.11,г показана зависимость результата измерения Nqот значения измеряемой
величины U_ рассматриваемого ВИ Ц при отсутствии всех инструментальных
погрешностей, а также зависимость абсолютной погрешности дискретности ![]() от U_. Как видно,
от U_. Как видно,
![]()
![]() (1.8)
(1.8)
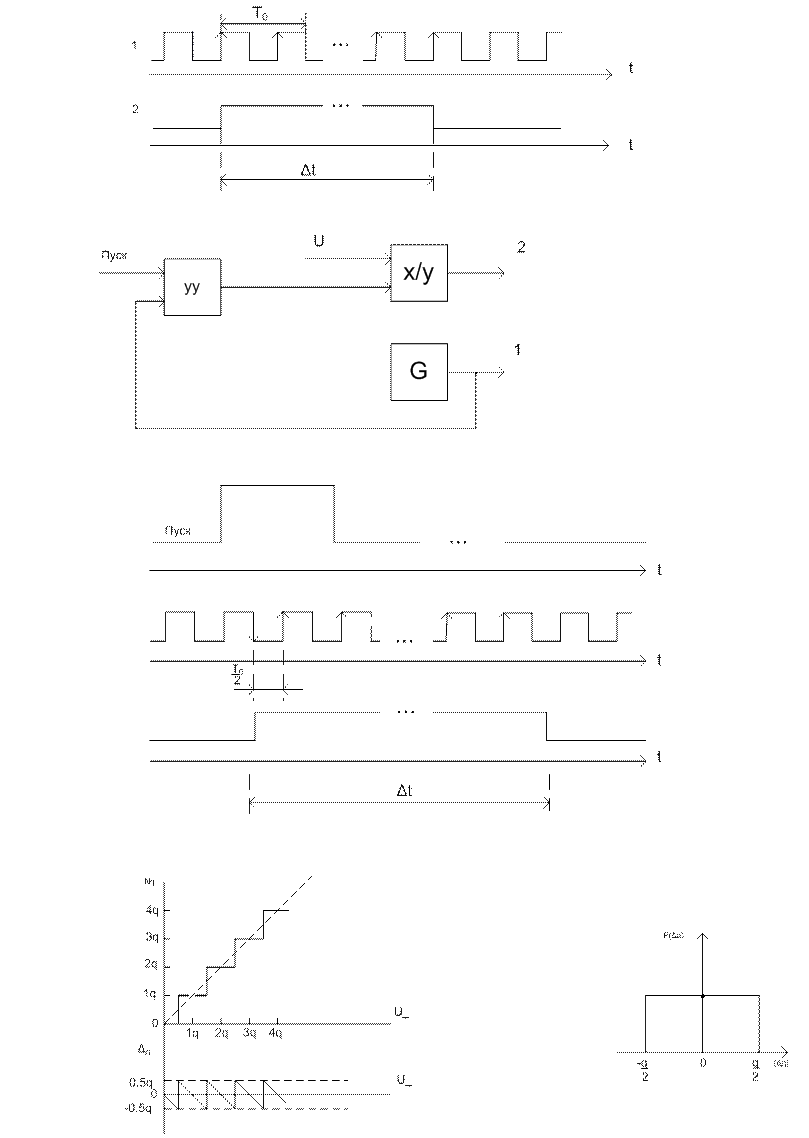
Рис. 1.11
Относительная и приведенная погрешности дискретности соответственно определяются формулами
![]()
![]() (1.9)
(1.9)
![]()
![]() (1.10)
(1.10)
Формулы (1.8)-(1.10) справедливы не только для ВИ ЦВ, но и для любых ЦИП и АЦП; то же самое можно сказать и о рис 1.11, г, если по оси абсцисс откладывать не U_, а любую измеряемую(преобразуемую) величину Х.
Пример. Для ЦВ с диапазоном измерения ![]() В имеем Uном=1 В; q=10
мкВ; Nном=105, следовательно,
В имеем Uном=1 В; q=10
мкВ; Nном=105, следовательно, ![]() мкВ;
мкВ; ![]()
Всю совокупность значений погрешности
дискретности можно рассматривать как функцию случайной величины, а именно –
значений измеряемой величины Х. Естественно считать, что значения Х
в пределах каждого кванта равновероятны. Тогда закон распределения погрешности
дискретности – это закон равномерной плотности. На рис. 1.11,д показана
плотность распределения абсолютной погрешности дискретности ![]()
График симметричен относительно оси ординат, т. е. математическое ожидание погрешности дискретности
![]()
а дисперсия определяется выражением
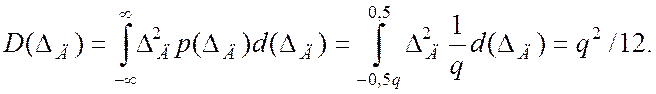 (1.11)
(1.11)
Соответственно среднее квадратическое отклонение
![]() .
(1.12)
.
(1.12)
Из (1.8) — (1.12) следует, что все характеристики погрешности дискретности известны, если известны qи Nном. Эти характеристики не требуют экспериментальной проверки.
Перейдем теперь к инструментальным погрешностям
и вернемся к ВИ ЦВ. Из двух инструментальных погрешностей этого ЦВ, а
именно ![]() — от
несовершенства генератора импульсов Gи
— от
несовершенства генератора импульсов Gи ![]() —от несовершенства преобразователя U_ в
—от несовершенства преобразователя U_ в ![]() (рис. 1.11,б),рассмотрим только
(рис. 1.11,б),рассмотрим только ![]() , считая
, считая ![]() .
Несовершенство Gпроявляется в том, что из-за некоторой неточности
установки и нестабильности действительное значение частоты импульсов сигнала 1
несколько отличается от номинального:
.
Несовершенство Gпроявляется в том, что из-за некоторой неточности
установки и нестабильности действительное значение частоты импульсов сигнала 1
несколько отличается от номинального:
![]()
Это приводит к тому, что действительное значение кванта этого ЦВ тоже будет несколько отличаться от номинального.
В самом деле, для этого ЦВ имеем
![]()
где S — коэффициент преобразования U_ в ![]() ;
;
![]()
Отсюда
![]()
Приближенность равенств в последних двух формулах
связана с тем, что в них не учитывается погрешность дискретности ![]() .
.
При f0=f0ном и S=Sном имеем q=qном, но при ![]() и S=Shom квант
и S=Shom квант ![]() , Пусть для
определенности
, Пусть для
определенности ![]() ,
тогда
,
тогда ![]() .
В этом случае
.
В этом случае
![]()
следовательно, общая абсолютная погрешность
![]()
На рис. 1.12,а показана зависимость результатов
измерения qномN от
значений U_ для нескольких первых
квантов с учетом ![]() , а на рис.
1.12,6 — с учетом только
, а на рис.
1.12,6 — с учетом только ![]() . Из рисунка видно, что наличие
. Из рисунка видно, что наличие ![]() соответствует
изменению наклона прямой линии, выражающей функцию преобразования ЦИП, по
отношению к номинальной. Такая погрешность называется мультипликативной. В
общем случае инструментальная погрешность ЦИП может содержать, три
составляющие: мультипликативную, аддитивную и нелинейную (рис. 1.13).
Аддитивная соответствует параллельному смещению прямой линии, выражающей
функцию преобразования ЦИП, по отношению к ее номинальному положению (рис.
1.13,г), а нелинейная — отклонению от прямолинейности (рис. 1.13,ж).
Абсолютное (
соответствует
изменению наклона прямой линии, выражающей функцию преобразования ЦИП, по
отношению к номинальной. Такая погрешность называется мультипликативной. В
общем случае инструментальная погрешность ЦИП может содержать, три
составляющие: мультипликативную, аддитивную и нелинейную (рис. 1.13).
Аддитивная соответствует параллельному смещению прямой линии, выражающей
функцию преобразования ЦИП, по отношению к ее номинальному положению (рис.
1.13,г), а нелинейная — отклонению от прямолинейности (рис. 1.13,ж).
Абсолютное (![]() )
и приведенное (
)
и приведенное (![]() )
значения мультипликативной составляющей линейно зависят от значений измеряемой
величины X(рис. 1.13,6), а относительное значение (
)
значения мультипликативной составляющей линейно зависят от значений измеряемой
величины X(рис. 1.13,6), а относительное значение (![]() ) не зависит (рис. 1.13,в).
) не зависит (рис. 1.13,в).
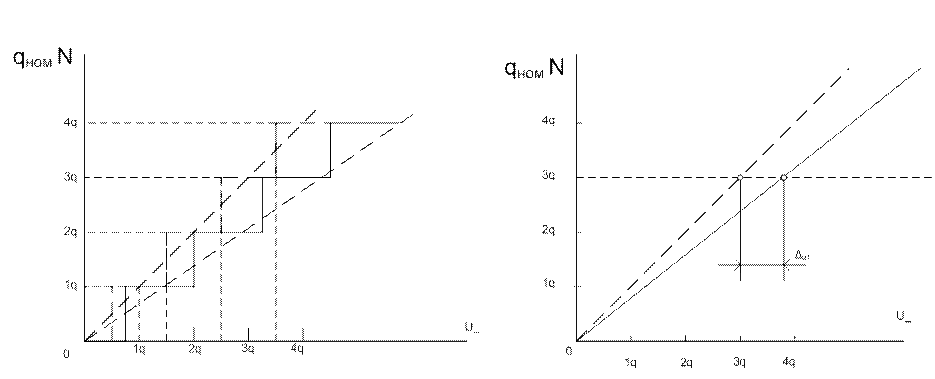 Рис. 1.12. Зависимость
результатов измерения от значений измеряемого напряжения.
Рис. 1.12. Зависимость
результатов измерения от значений измеряемого напряжения.
У аддитивной
составляющей, напротив, абсолютное (![]() )
и приведенное (
)
и приведенное (![]() )
значения не зависят от X(рис. 1.13,д), а ее относительное значение
(|6и.а) обратно пропорционально X, поэтому аддитивная
составляющая как бы «хуже» мультипликативной: при
)
значения не зависят от X(рис. 1.13,д), а ее относительное значение
(|6и.а) обратно пропорционально X, поэтому аддитивная
составляющая как бы «хуже» мультипликативной: при ![]()
![]() У нелинейной составляющей все три ее значения
У нелинейной составляющей все три ее значения ![]() ,
, ![]() и
и ![]() (рис. 1.13,з,
и) нелинейно зависят от X. На рис. 1.13,ж Показана монотонная
нелинейность. В некоторых случаях, например, в кодоимпульсных ЦИП, она может
иметь гораздо более сложный характер, с неравномерными скачками и разрывами.
(рис. 1.13,з,
и) нелинейно зависят от X. На рис. 1.13,ж Показана монотонная
нелинейность. В некоторых случаях, например, в кодоимпульсных ЦИП, она может
иметь гораздо более сложный характер, с неравномерными скачками и разрывами.
Само название «нелинейная» не требует пояснений. Заметим только, что если говорить о ней как о самостоятельной погрешности, то лучше пользоваться термином «погрешность линейности» или «погрешность из-за нелинейности».
Что же касается названий «мультипликативная» и «аддитивная», то они требуют пояснения. Если считать, что нелинейная составляющая отсутствует, то результат цифрового измерения можно представить в виде
![]()
Откуда видно, что учет мультипликативной погрешности требует умножения (miltiply), а аддитивной – добавления add. Здесь уместно ненадолго вернуться к погрешности дискретности, чтобы выяснить, нельзя ли и ее отнести к какому-либо из трех видов, как и составляющие инструментальной погрешности.
Если рассматривать всю совокупность возможных её значений в соответствии с рис. 1.11,в (1.8)-(1.10), то её можно назвать погрешностью линейности, если же брать только максимально возможные значения, то сами они имеют аддитивный характер, причем это симметричная двухзначная аддитивность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.