Основные технические характеристики ЦИП и АЦП, страница 3

 Рис 1.13.

.

Рис. 1.14.

Аддитивная и мультипликативная составляющие инструментальной погрешности существенно снижаются после выполнения двух операций, называемых «установка нуля» и «калибровка» (рис. 1.14). Первая из них состоит в том, что при Х=0 (например, для ЦВ при замкнутых накоротко входных зажимах) специальной регулировкой устанавливают нулевое показание ЦИП(N=0), а при второй на вход подается известное калибровочное значение Х=Х_к  и другой специальной регулировкой устанавливается соответствующее показание N=N_k.

Остается  нелинейность – её нужно обеспечить на достаточно низком уровне при проектировании прибора, и остается погрешность дискретности (на рис. 1.14 не показана) – её устранить принципиально невозможно.

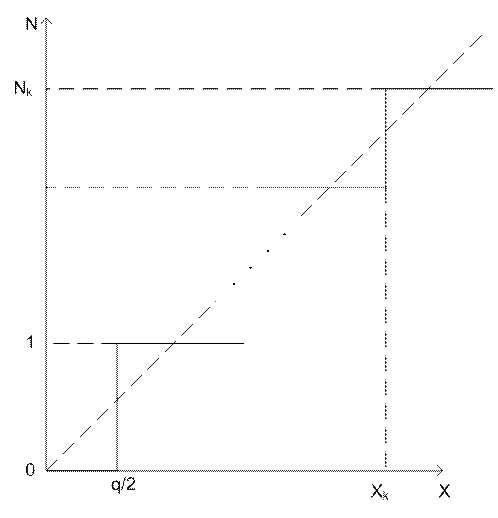
Рис. 1.14.

Процедура установки нуля и калибровки описана в предположении, что общая погрешность  существенно превышает максимальную погрешность дискретности, во всяком случае составляет нескольких квантов q. Так обычно и бывает в цифровых вольтметрах и других цифровых приборах. Однако в некоторых случаях  близка к– в цифровых частотомерах, в аналого-цифровых преобразователях, причем к последним иногда предъявляется требование, чтобы не превышала  в рабочих условиях эксплуатации. В этих случаях процедуру установки нуля и калибровки нужно приводить немного сложней (рис. 1.15). Для установки нуля нужно подать сигнал

X=X₀= 0,5q_ном

и регулировкой добиться такой ситуации, чтобы происходила смена показаний от N=0 к N=1 и обратно. При калибровке нужно подать сигнал

X=X_k=(N_k-0,5)q_ном

и другой регулировкой добиться смены показаний от N=N_k-1 к N=N_k и обратно.

Наличие случайной составляющей инструментальной погрешности приводит к тому, что значения Х₀ и Х_к, при которых происходят переходы  и , получаются несколько «размытыми», т. е. находятся в некоторых диапазонах. Пользуясь двумя регулировками, желательно установить их в положения, примерно соответствующие серединам этих диапазонов.

Однако полностью устранить аддитивную и мультипликативную составляющие инструментальной погрешности не удается по следующим причинам:

а) калибровочное значение Х_к само имеет некоторую погрешность относительно его номинала N_kq_ном;

б) и  изменяются во времени, а измерение может производиться не сразу после установки нуля и калибровки;

в) условия, при которых производиться измерение (температура окружающей среды, напряжение питание и др.), могут отличаться от условий, при которых производились установка нуля и калибровка;

г) в ЦИП с несколькими диапазонами измерения калибровка производится на одном из них, а измерение – на любом.

В АЦП, работающих в системах с ЭВМ, а также в ЦИП, содержащих микропроцессор, есть и другой, более эффективный путь снижения влияния аддитивной и мультипликативной составляющих без всяких регулировок. Он состоит в том, что автоматически через определенные промежутки времени в память ЭВМ или микропроцессора вводятся два числа N₀ и N_k, соответствующие подключению Х=0 и Х=Х_к. Из-за аддитивной и мультипликативной составляющих  и N_k=N_к.ном.. В памяти хранится также число N_к.ном. К каждому результату измерения N автоматически вводится поправка; поправленный результат вычисляется по формуле

N’=N_к.ном(N-N₀)/(N_к-N₀).

Автоматическое обновление чисел N₀ и N_k может производиться достаточно часто, поэтому уменьшается влияние факторов, отмеченных выше в пп. «б» и «в».

Применяются, конечно, и технологические способы снижения и : точные и стабильные резисторы, высококачественные усилители, термостатирование наиболее ответственных элементов и т.п.

Несмотря на все меры некоторый уровень ,  и  остаются. Нормируется обычно общая погрешность в виде предела допускаемой абсолютной (), или приведенной (), или относительной () погрешности.

Если бы у прибора была только аддитивная составляющая, то можно было бы задать  или в виде одного числа, например мкВ или; если бы была только мультипликативная, то можно было задать  в виде одного числа. Но в действительности есть все три составляющие. Как же тогда задать предел допускаемой погрешности? Можно, конечно, и в этом случае задать его в виде одного числа, например мкВ (рис 1.16) для цифрового вольтметра. Однако это невыгодно, потому что при этом характеризуем прибор хуже, чем он есть на самом деле: в заштрихованной зоне

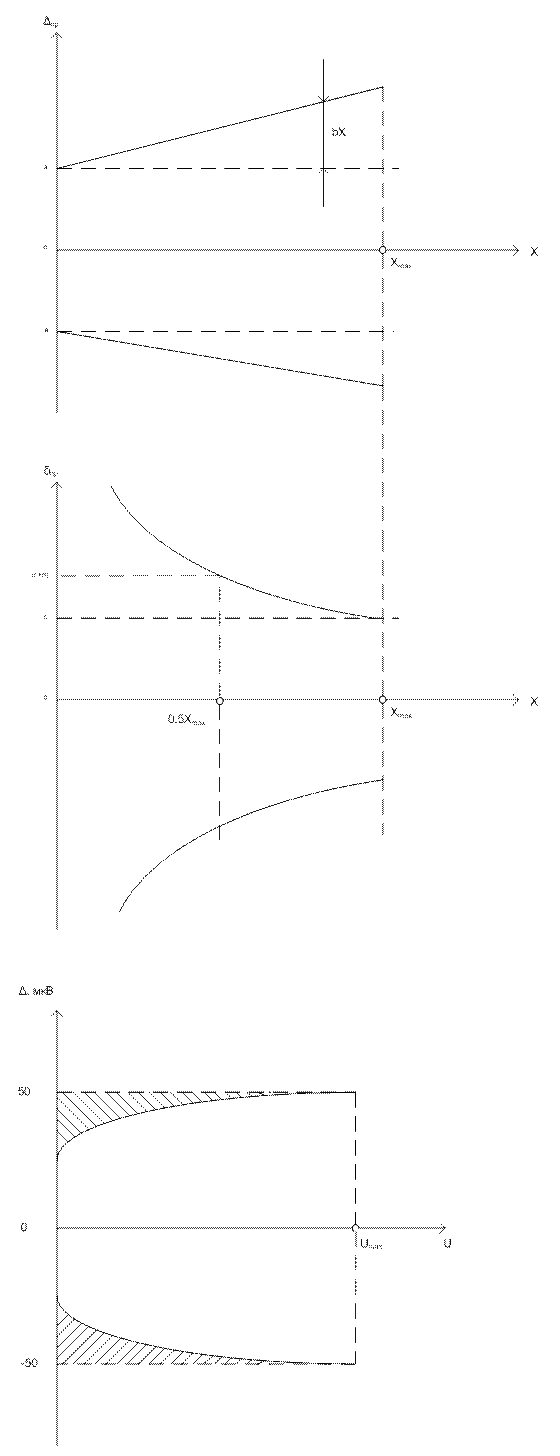Рис. 1.15.

не бывает значений погрешности. Поэтому для сравнительно дорогих и сложных приборов, к которым относятся ЦИП, применяют более сложные формы выражения предела допускаемой погрешности: не в виде одного числа, а в виде функции, обычно самой простой – линейной (рис. 1.17,а)

,

или (рис. 1.17, б) в процентах

Причем с-d=100b;

Согласно [14] при нормировании в форме (1.15) класс точности обозначается в виде дроби c/d, например 0,01/0,005, причем числа c и  dвыбираются из ряда [1; 1,5; (1,6); 2; 2,5; (3); 4; 5; 6]*10^k, где k=1; 0; -1; -2 и т.д. Значения в круглых скобках не рекомендуемы.

Если бы отсутствовала нелинейная составляющая, то коэффициенты b или (c-d) в (1.14), (1.15) соответствовали бы мультипликативной составляющей, а a и d – сумме аддитивной составляющей и погрешности дискретности. Если бы вообще отсутствовала инструментальная погрешность, то было бы

b=0;

Иностранные фирмы нормируют точность ЦИП в несколько иной форме, например

,

где R-reading(показание); FS-fullscale(полная шкала).

Пусть эти данные относятся к цифровому вольтметру с диапазоном измерения от 0 до 1, 1999 В. Если бы это был отечественный прибор, то в соответствии с [14] его точность в процентах следовало бы нормировать в виде

,

где U-в вольтах.

Можно проверить, нет ли противоречия в этих данных: сомножитель 0,01 должен быть заведомо больше максимальной приведенной погрешности дискретности. Для данного прибора в соответствии с (1.10) имеем

,

т.е противоречия нет.

Для ЦИП с несколькими диапазонами измерения могут нормироваться разные значения основной погрешности и изменений показаний на разных диапазонах. В табл. 1.6 приведен соответствующий пример: по (1.15) вычислены значения предела основной погрешности  на границах диапазонов цифрового вольтметра.

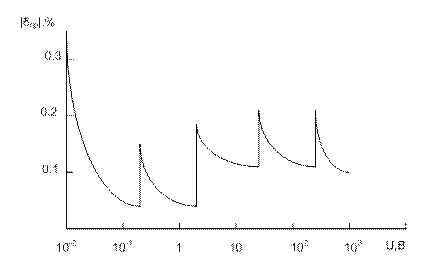
Рис. 1.18

Зависимость  показана на рис. 1.18 в логарифмическом масштабе по оси абсцисс. На рисунке не показан начальный участок 1-го диапазона (мВ), где при .

Выше отмечалось, что иностранные фирмы при нормировании точности выражают погрешность в форме, отличающейся от принятой в СССР. Более существенным является отличие в самих условиях нормирования. Иностранные фирмы обычно не пользуются понятиями основной погрешности и изменений показаний под действием влияющих факторов. Они гарантируют одно или несколько значений предела допустимой погрешности для определенного комплекса условий эксплуатации прибора, например