Другие предметы \ Основы метрологии и теории измерений

Критерий Смирнова для определения промахов в выборке. Параметрические критерии

Страницы работы

12 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Содержание работы

Критерий Смирнова
        Применяется для определения промахов в выборке в предположении нормального распределения случайной измеренной величины, для которой генеральные параметры неизвестны, а известны лишь их оценки, полученные по выборочным результатам наблюдений.

1.  Определить случайные отклонения: .

2.  Определить оценку среднего квадратического отклонения результатов наблюдений: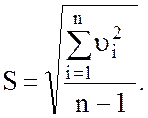

3.  Определить отношение максимального по модулю значения случайного отклонения к оценке СКО и сравнить с допустимым из таблицы: 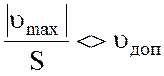. Если частное меньше , то проверяемое значение промахом не является, если больше, то проверяемое значение – промах, которое необходимо исключить из выборки и пересчитать оценку САЗ и СКО.

n
q = 0,10 (Pдов = 0,90)
q = 0,05 (Pдов = 0,95)
q = 0,01 (Pдов = 0,99)
3
1,15
1,15
1,15
4
1,42
1.46
1.49
5
1,60
1,67
1,75
6
1,73
1,82
1,94
7
1,83
1,94
2,10
8
1,91
2,03
2,22
9
1,98
2,11
2,32
10
2,03
2,18
2,41
11
2,09
2,23
2,48
12
2,13
2,29
2,55
13
2,17
2,33
2,61
14
2,21
2,37
2,66
15
2,25
2,41
2,70
16
2,28
2,44
2,75
17
2,31
2,48
2,78
18
2,34
2,50
2,82
19
2,36
2,53
2,85
20
2,38
2,56
2,88
21
2,41
2,58
2,91
22
2,43
2,60
2,94
23
2,45
2,62
2,96
24
2,47
2,64
2,99
25
2,49
2,66
3,01
30
2,70
2,93
3,40
40
2,79
3,02
3,48
50
2,86
3,08
3,54
100
3,08
3,29
3,72
250
3,34
3,53
3,95
500
3,53
3,70
4,11
Распределение Стьюдента

k/Pдов

0.80

0.90

0.95

0.98

0.99

0.995

0.999

1

3.08

6.31

12.71

31.82

63.66

127.32

636.62

2

1.89

2.92

4.30

6.93

9.53

14.09

31.60

3

1.64

2.35

3.18

4.54

5.84

7.45

12.94

4

1.53

2.13

2.78

3.75

4.60

5.60

8.61

5

1.48

2.02

2.57

3.37

4.03

4.77

6.86

6

1.44

1.94

2.45

3.14

3.71

4.32

5.96

7

1.42

1.90

2.37

3.00

3.50

4.03

5.41

8

1.40

1.86

2.31

2.90

3.36

3.83

5.04

9

1.38

1.83

2.26

2.82

3.25

3.69

4.78

10

1.37

1.81

2.23

2.76

3.17

3.58

4.59

11

1.36

1.80

2.20

2.72

3.11

3.50

4.44

12

1.36

1.78

2.18

2.68

3.06

3.43

4.32

13

1.35

1.77

2.16

2.651

3.01

3.37

4.22

14

1.34

1.76

2.15

2.62

2.98

3.33

4.14

15

1.34

1.75

2.13

2.60

2.95

3.29

4.07

16

1.34

1.75

2.12

2.58

2.92

3.25

4.02

17

1.33

1.74

2.11

2.57

2.90

3.22

3.97

18

1.33

1.73

2.10

2.55

2.88

3.20

3.92

19

1.33

1.73

2.09

2.54

2.86

3.17

3.88

20

1.33

1.73

2.09

2.53

2.85

3.15

3.85

21

1.32

1.72

2.08

2.52

2.83

3.14

3.82

22

1.32

1.72

2.07

2.51

2.82

3.12

3.79

23

1.32

1.71

2.07

2.50

2.81

3.10

3.77

24

1.32

1.71

2.06

2.49

2.80

3.09

3.75

25

1.32

1.71

2.06

2.48

2.79

3.08

3.73

26

1.32

1.71

2.06

2.48

2.78

3.07

3.71

27

1.31

1.70

2.05

2.47

2.77

3.06

3.69

28

1.31

1.70

2.04

2.46

2.76

3.05

3.67

29

1.31

1.70

2.04

2.46

2.76

3.04

3.66

30

1.31

1.70

2.04

2.46

2.75

3.03

3.65

40

1.30

1.68

2.02

2.42

2.70

2.97

3.55

60

1.30

1.67

2.00

2.39

2.66

2.91

3.46

90

1.29

1.66

1.98

2.36

2.62

2.86

3.37

120

1.28

1.64

1.96

2.33

2.58

2.81

3.29

Число степеней свободы определяют какk=n –1,   K=N–m, К =n–m,

где  n - количество измерений в выборке;

N - суммарное количество измерений в нескольких сериях (объединяемых) при неравноточных измерениях;

m – количество серий (выборок) при неравноточных измерениях

Похожие материалы

Информация о работе

ВУЗ:
Национальный аэрокосмический университет имени Н. Е. Жуковского (ХАИ)
Предмет:
Основы метрологии и теории измерений
Тип:
Задания на контрольные работы
Категория:
Другие предметы (Технические предметы)
Размер файла:
378 Kb
Скачали:
0
Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.