Критерий Смирнова для определения промахов в выборке. Параметрические критерии, страница 3

m	Уровень значимости  q = 0,01(Рдов = 0,99)
3	0,8335	7933	7606	7335	7107	6912	6743	6059	5153
4	7212	6761	6410	6129	5897	5702	5536	4884	4057
5	6329	5875	5531	5259	5037	4854	4697	4094	3351
6	5635	5195	4866	4608	4401	4229	4084	3529	2858
7	5080	4659	4347	4105	3911	3751	3616	2105	2494
8	4627	4226	3932	3704	3522	3373	3248	2779	2214
9	4251	3870	3592	3378	3207	3067	2950	2514	1992
10	3934	3572	3308	3106	2945	2813	2704	2297	1811
12	3428	3099	2861	2680	2535	2419	2320	1961	1535
15	2882	2593	2386	2228	2104	2002	1918	1612	1251
20	2288	2048	1877	1748	1646	1567	1504	1248	0960
24	1978	1759	1608	1495	1406	1338	1283	1060	0810

    m– количество объединяемых групп (серий, выборок) измерений

k – число степеней свободы: k= n-1,   

где  n – число результатов в выборке (группе, серии) 

Проверка распределения результатов наблюдений в выборке

на соответствие нормальному закону распределения

        При малом числе результатов наблюдений в выборке (n не более 61) соответствие их распределения нормальному закону проверяют при помощи составного  d - критерия.

        Критерий 1.   Вычисляют отношение  

,

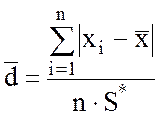где  n – количество результатов наблюдений в выборке,

       х_i – результат наблюдения,  – среднее арифметическое значение,

      – смещенная оценка среднего квадратического отклонения:

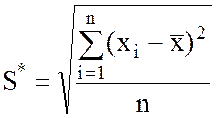
        Результаты наблюдений выборки можно  считать распределенными нормально, если:

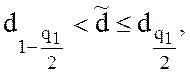
где 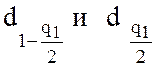  -  квантили распределения, выбираемые из таблицы статистики d, по количеству наблюдений в выборке n,   и , причем  q₁ – заранее выбранный уровень значимости критерия.

Статистика d

n	()100%		100%
	1%	5%	95%	99%
16 21 26 31 36 41 47 51 61	0,9137 0,9001 0,8901 0,8826 0,8769 0,8722 0,8682 0,8648 0,8574	0,8884 0,8768 0,8686 0,8625 0,8578 0,8540 0,8508 0,8481 0,8422	0,7236 0,7304 0,7360 0,7404 0,7440 0,7470 0,7496 0,7518 0,7596	0,6829 0,6950 0,7040 0,7110 0,7167 0,7216 0,7256 0,7291 0,7366

Критерий 2.  Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m  разностей    превзошли   значение  (∙ S) .

Параметрические критерии

    Применяют для определения соответствия закона распределения случайных величин нормальному при малых выборках, когда построение гистограммы или кривой распределения нецелесообразно. При этом рассчитывают отдельные параметры распределения – коэффициент асимметрии и коэффициент эксцесса. Первый характеризует несимметричность распределения, второй – остро- или плосковершинность кривой распределения.

1. Коэффициент асимметрии:

     ;         .       

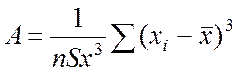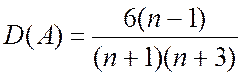     Если , то по данному параметру распределение можно признать нормальным.

2. Коэффициент эксцесса:

    ;       .    

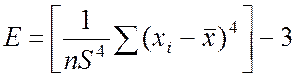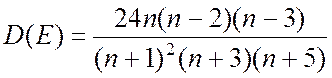Если  , то по данному параметру распределение можно признать нормальным.

Распределение  коэффициента  корреляции  R

Коэффициент корреляции может принимать значения 0 < R < 1.

Число степе-ней свободы k = n - 1	Уровень значимости, q
	0,10	0,05	0,02	0,01	0,001
2	0,900	0,950	0,980	0,990	0,999
3	0,805	0,878	0,934	0,959	0,992
4	0,729	0,811	0,882	0,917	0,974
5	0,669	0,754	0,833	0,874	0,951
6	0,621	0,707	0,789	0,834	0,925
7	0,582	0,666	0,750	0,798	0,898
8	0,549	0,632	0,716	0,765	0,872
9	0,521	0,602	0,685	0,735	0,847
10	0,497	0,576	0,658	0,708	0,823
12	0,457	0,532	0,612	0,661	0,780
14	0,426	0,497	0,574	0,623	0,742
16	0,400	0,468	0,543	0,590	0,708
18	0,389	0,456	0,528	0,561	0,679
20	0,369	0,433	0,503	0,549	0,665
25	0,323	0,381	0,445	0,487	0,597
30	0,296	0,349	0,409	0,449	0,554
35	0,275	0,325	0,381	0,418	0,519
40	0,257	0,304	0,358	0,393	0,490
45	0,248	0,287	0,338	0,372	0,465
50	0,231	0,273	0,322	0,354	0,443
60	0,211	0,250	0,295	0,325	0,408
70	0,195	0,232	0,274	0,302	0,380
80	0,183	0,217	0,256	0,283	0,357
90	0,173	0,205	0,242	0,264	0,337
100	0,164	0,195	0,230	0,254	0,321