Механика грунтов: Методические указания к выполнению курсовой работы, страница 3

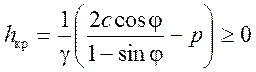
образуется участок отрицательного давления грунта на стенку (см. рис. 4.2). Принято, однако, считать, что удельная сила прилипания грунта к стенке мала и поэтому участок эпюры с растягивающим напряжением реализовываться не может. На участке  принимают = 0, в результате чего оказывается, что этот слой грунта не приходит в предельное состояние. В сыпучем грунте (с = Н = 0) эта проблема не возникает – эпюра активного давления треугольной формы и всюду положительна ( = 0).

          Результирующая активного давления на один метр длины стенки в случае, когда эпюра имеет вид треугольника > 0, определяется площадью треугольника давления:

,

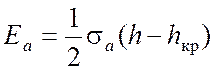где — высота стенки;  – активное давление на уровне подошвы стенки (.

          Линия действия ее проходит через центр тяжести треугольника давления, т.е. на расстоянии 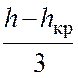 от уровня подошвы стенки.

Рис. 4.2. Расчетная схема к расчетам устойчивости стенки против сдвига и опрокидывания

4.2. Расчет устойчивости стенки против сдвига в плоскости подошвы

          Если активное давление достаточно велико, то оно может сдвинуть подпорную стенку в горизонтальном Направлении, так что произойдет сдвиг подошвы стенки по грунту. Такому смещению стенки препятствуют силы пассивного отпора грунта и силы трения подошвы стенки о грунт. По причине шероховатости подошвы стенки принято считать, что в плоскости подошвы происходит сдвиг грунта по грунту. Поэтому сила трения по подошве определяется в соответствии с законом Кулона по формуле

T=Gtgφ₀+c₀b,(4.7)

где G– вес стенки.        

          Для подсчета веса подпорной стенки ее поперечное сечение удобно разделить на элементарные фигуры: прямоугольники и треугольники, как показано на рис. 4.2. Вес любой такой части на единицу длины стенки определяется произве­дением

G_i = γ_бA_i,                                                                                  (4.8)

где А_i– площадь соответствующей фигуры.

          Степень устойчивости стенки против сдвига может быть оценена по коэффициенту запаса устойчивости

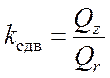,                                                                (4.9)

где Q_z, Q_r– результирующие удерживающих и сдвигаю­щих сил:

.                                                                                  (4.10)

          Стенка устойчива против сдвига, если выполняется условие [2]

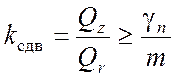,                                                       (4.11)

где γ_n – коэффициент надежности по назначению сооружения, принимаемый равным 1,1; т – коэффициент условий работы, принимаемый равным 0,9.

4.3 Расчет устойчивости стенки против опрокидывания

          При достаточно больших высоте подпорной стенки и величине активного давления может произойти опрокидывание стенки относительно переднего ребра фундаментной плиты (точка А₁на рис. 4.2). Очевидно, опрокинуть стенку стре­мятся силы активного давления Е_а' и Е_а", удерживают от опрокидывания силы собственного веса стенки G₁, G₂, G₃ и силы пассивного давления Е_p' и Е_p". Степень устойчивости стенки против опрокидывания оценивается коэффициентом запаса устойчивости

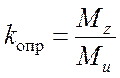,                                                               (4.12)

где М_z, М_и – момент удерживающих и момент опрокидывающих сил:

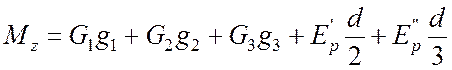 ;                                                (4.13)

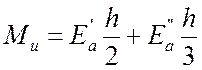 ,                                                                                                   (4.14)

здесь g_i – плечи сил G_i, относительно точки А₁.

          Стенка устойчива против опрокидывания, если выполняется условие [2]

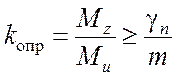,                                                                          (4.15)

где коэффициенты надежности и условий работы  принимаются равными:  γ_n= 1,1, m = 0,8.

4.4. Расчет устойчивости основания стенки против сдвига по круглоцилиндрическим поверхностям скольжения

          Помимо потери устойчивости самой подпорной стенки при большой нагрузке может произойти потеря устойчивости ее основания. В практике проектирования широко применяется проверка возможности потери устойчивости основания посредством сдвига по круглоцилиндрической поверхности скольжения. В полном объеме расчет этот трудоемок, поскольку требуется выполнить целый ряд проверок устойчивости по различным поверхностям скольжения, чтобы определить наиболее опасную круглоцилиндрическую поверх­ность скольжения и соответствующий ей наименьший коэффициент запаса устойчивости [1].

          В курсовой работе этот расчет выполняется в сокращенном объеме и до некоторой степени в упрощенном виде.

          При этом студенты специальности «Тоннели и метрополитены» выполняют проверки по трем поверхностям скольжения с тремя центрами вращения С₁ С₂, С₃, а студенты специальности «Строительство железных дорог» – только по одной поверхности с центром вращения С₂ (рис. 4.3).

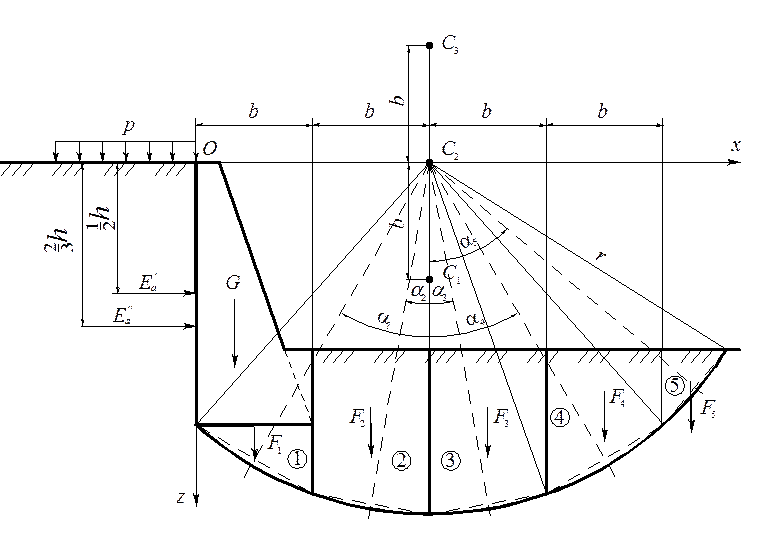
Рис. 4.3. Схема к расчету устойчивости основания стенки

          Поскольку излагаемый метод расчета относится к графоаналитическим методам, то точность его зависит, в частности, от масштаба и аккуратности выполнения расчетной схемы.

          Проверка устойчивости основания на сдвиг по каждой круглоцилиндрическои поверхности скольжения, выполняется в следующей последовательности.

          На расчетной схеме, вычерченной в подходящем масштабе, с помощью циркуля из выбранного центра вращения проводится круглоцилиндрическая линия скольжения (см. рис. 4.3). Выделенный ею сегмент вертикальными линиям делится на ряд отсеков. В курсовой работе рекомендуется выделить пять отсеков, как показано на рис. 4.3. Определяются площади отсеков A_iи их вес F_i=γ₀ A_i. При подсчете площадей разрешается необходимые размеры определять по чертежу, а дуги линий скольжения при этом заменять хордами.

          Устойчивость основания против сдвига по круглоцилиндрической поверхности оценивается величиной коэффициента запаса устойчивости

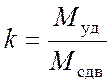,                                                      (4.16)

М_уд , М_сдв – моменты удерживающих и сдвигающих сил относительно центра вращения.

          Чтобы определить моменты удерживающих и сдвигающих сил, рассмотрим два отсека: один из левой части сегмента, другой из правой (рис. 4.4). Разложим силу веса F, действующую на отсек, на. нормальную N_iи касательную Q_iсоставляющие: