7.Обоснование неснижаемого оборота фонда запасных частей на складе депо.
разработка математической модели функционирования склада;
поиск такой величины запаса, при которой доход от работы склада будет максимальным.
В настоящей дипломной работе будем считать, что математическая модель задана в виде следующей системы алгебраических уравнений:
m * РN - l * РM = 0; j = M
m * Рj - K - l * Рj + l * Рj
+ 1 = 0; j ![]() (N, M).
(N, M).
2m * РN - K - (l + m) * РN + m * Р0 + l * РN + 1 = 0; j = N.
2m * Рj-K – (l + m) * Рj + l * Рj
+ 1 = 0; j ![]() ((n - 2)k,(n -
1)k) (7.1)
((n - 2)k,(n -
1)k) (7.1)
(n – i) * m * Рj -K – [l + (n – 1 – i) * m] * Рj + l * Рj + 1 = 0;
j ![]() (I * k, (i + 1) * k]; i = 1, n - 3
(I * k, (i + 1) * k]; i = 1, n - 3
- [l + (n – 1) * m] * Рj + l * Рj
+ 1 = 0; j ![]() (0,k]
(0,k]
- m * Р0 + l * Р1 = 0; j = 0.
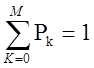 (7.2)
(7.2)
Здесь: Рj – вероятность того, что в каждый взятый момент времени на складе находится ровно j запасных частей;
m - параметр закона обслуживания (m=1/Т2);
Т2 – среднестатистическая периодичность пополнения запасов склада;
l - интенсивность изъятия деталей из склада в ремонт, (l=1/ Т1);
Т1 – среднестатистическая периодичность изъятия деталей из склада;
N – емкость пакета большого объема;
k - емкость пакета малого объема;
М – емкость склада в штуках;
n - емкость склада в пакетах;
j – количество деталей на складе (в штуках);
Как
видно из рисунка 7.1, для любого момента времени выполняется условие баланса: u + ![]() = n – емкость склада в пакетах.
= n – емкость склада в пакетах.
Примем: N = (n-1) * k, М = n * k;
Самым трудоемким этапом является решение системы (7.1) при ограничении (7.2).
Временно предположим, что известна вероятность Р0. Тогда из последнего уравнения рассматриваемой системы определим значение Р1:
Р1 = (m/l) * Р0;
Где S – среднее число запчастей, изъятых со склада в ремонт за время Т2 (S = l * (1 – P0) * T2);
q –эффект от того, что в нужный момент “под рукой” оказалась требуемая запасная деталь (q = 25000 у.е.);
С – затраты на хранение детали в течении Т2 (С = 3000у.е.);
Mx = 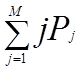 - математическое
ожидание числа деталей находящихся на складе.
- математическое
ожидание числа деталей находящихся на складе.
Идея оптимизации состоит в следующем. Зададимся множеством пар (k,n). Для каждой из них опираясь на уравнения (7.1, 7.2). а также на значения l и m, получим значение целевой функции П (М), где М = n * k.
Приведем технологию расчета значение целевой функции при k=2 и n=4.
Таким образом, для организации этих расчетов введем две таблицы.
|
Р1 |
а1Р0 |
|
а1 |
r |
|
|||
|
Р2 |
а2Р0 |
0,017919 |
а2 |
а1(1+3r) |
1,68 |
|||
|
Р3 |
а3Р0 |
0,050173 |
а3 |
а2(1+3r) |
4,704 |
|||
|
Р4 |
а4Р0 |
0,098862 |
а4 |
а3(1+2r)-3а1r |
9,2688 |
|||
|
Р5 |
а5Р0 |
0,185242 |
а5 |
а4(1+2r)-3а2r |
17,36736 |
|||
|
Р6 |
а6Р0 |
0,236179 |
а6 |
а5(1+r)-2а3r |
22,142976 |
|||
|
Р7 |
а7Р0 |
0,252852 |
а7 |
а6(1+r)-2а4r-r |
23,706202 |
|||
|
Р8 |
а8Р0 |
0,141707 |
а8 |
а7-а5r |
13,285786 |
|||
|
Р0 |
Р0 |
0,010666 |
åак |
92,755123 |
||||
Зададимся значениями Т1, Т2:
Т1 = 4 суток, Т2 = 6,7 суток, r = 0,6, при к = 2 и n = 4
Временно допустим, что нам известно Р0.
Из последнего уравнения системы (7.1) определяем выражение для Р1:
Р1 = r * Р0
Обозначим а1 = r и занесем это значение а1 в таблицу 7.2, а выражение для Р1 (т.е. а1 Р0) – в таблицу 7.1.
Значения Р1 и Р2 определяем из второго снизу уравнения системы (7.1):
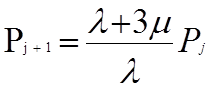
При j = 1
Р2 = (1 + 3r) Р1 = (1 + 3r) а1Р0 = а2Р0, где а2 = а1 (1 + 3r)
j = 2
Р3 = (1 + 3r) Р2 = (1 + 3r) а2Р0 = а3Р0, где а3 = а2 (1 + 3r)
Выражения для Р0 и Р0 получаем третьего снизу уравнения системы (7.1):
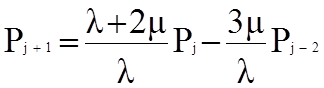
Пусть j =3
Р4 = (1 + 2r) Р3 - 3rР1 = [(1 + 2r) а3Р0 - 3r а1Р0] = а4Р0
Пусть j =4
Р5 = (1 + 2r) Р4 - 3rР2 = [(1 + 2r) а4Р0 - 3r а2Р0] = а5Р0
Выражение для Р6 найдём из четвертого уравнения снизу системы (7.1):
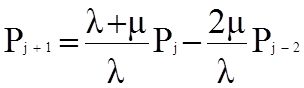
Пусть j =5
Р6 = [(1 + r) а5Р0 - 2r а3Р0] = а6Р0
Выражение для Р7 найдём из третьего уравнения сверху системы (7.1):
РN+1 = (1 + r) РN - rРN-2 - rР0,
т.к. N = (n – 1) * к = 6, то
Р7 = (1 + r)а6Р0 - 2r а4Р0 - rР0 = а7Р0
Выражение для Р8 получаем из второго уравнения сверху системы (7.1):
Рj+1 =Рj - rРj-2
При j =7 имеем:
Р8 = а7Р0 - r а5Р0 = а8Р0
Осталось определить выражение для Р0 из условия нормировки (7.2):
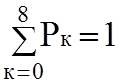
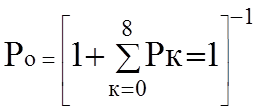
Р0 = 1/93,755 = 0,0107
Заполнив таблицы 7.1 и 7.2, получим значения Рj, где j = 0,1,2,…,8.
Затем по формуле (7.3) подсчитаем величину прибыли.
П(2,4) = 23716 у.е.
По аналогии рассматриваются другие варианты множества [к, n] (результаты сведены в таблицу 7.3).
Таблица 7.3
|
n |
k |
П(n, k) |
|
6 |
1 |
27575,8 |
|
6 |
2 |
12163,1 |
|
6 |
3 |
-4333,35 |
|
6 |
4 |
-20833,3 |
|
6 |
5 |
-37333,3 |
|
6 |
6 |
-51317,2 |
|
5 |
1 |
29109,21 |
|
5 |
2 |
18110,83 |
|
5 |
3 |
4665,843 |
|
5 |
4 |
-8833,35 |
|
5 |
5 |
-22333,3 |
|
4 |
1 |
28817,62 |
|
4 |
2 |
23716,91 |
|
4 |
3 |
13637,23 |
|
4 |
4 |
2704,462 |
|
3 |
1 |
28591,59 |
|
3 |
2 |
26830,38 |
|
3 |
3 |
21624,94 |
|
3 |
4 |
15019,25 |
Как видно из таблицы 7.3. наилучшим вариантом является пара (5,1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.