Полтавський державний педагогічний університет
ім. В. Г. Короленка
ПЛАН – КОНСПЕКТ УРОКУ
студентки групи Ф-51
Дорошенко Олени
План-конспект уроку
Тема: Теорема про три перпендикуляри
Теорема про три перпендикуляри, яку вивчають у 10-му класі, одна з важливих у курсі стереометрії. Вона знаходить широке застосування під час обчислення відстаней у просторі, зображення кутів між площинами та двогранних кутів.
Мета:
· ознайомити учнів з теоремою про три перпендикуляри;
· формувати вміння та навички використовувати теорему до розв'язування задач;
· вчити користуватися опорними фактами під час доведення тверджень і розв'язування задач;
· розвивати логічне мислення;
· виховувати активність, культуру мовлення і математичних записів.
Тип уроку: урок викладу нового матеріалу.
Обладнання: Моделі, таблиця, картки.
1. Організаційний момент. (2 хв.)
2. Актуалізація опорних знань. (10 хв.)
3. Вивчення нового матеріалу. (15 хв.)
4. Розв'язування задач на закріплення теореми. (10 хв.)
5. Підсумок уроку. (5 хв.)
6. Домашнє завдання. ( 3 хв.)
I. Організаційний момент.
II. Актуалізація опорних знань.
1. Фронтальне опитування класу:
а) сформулюйте означення, ознаку прямої, перпендикулярної до площини;
б) сформулюйте властивість медіани рівнобедреного трикутника, проведеної до основи;
в) назвіть залежність, яка існує між похилими, проведеними з однієї точки, та їх проекціями.
2. Розв'язування біля дошки трьома учнями задач, записаних на картках.
Точка віддалена від усіх вершин правильного трикутника на 5 дм. Медіана цього трикутника дорівнює 6 дм. Знайдіть відстань від даної точки до ллошини трикутника
Нехай АВС — даний трикутник, точка М така, що МО![]() (АВС).
(АВС).
Тоді АМ = ВМ = CM = 5 (дм). Точка О — центр кола, описаного навколо ![]() AВC, є точкою перетину медіан, висот
і бісектрис.
AВC, є точкою перетину медіан, висот
і бісектрис.
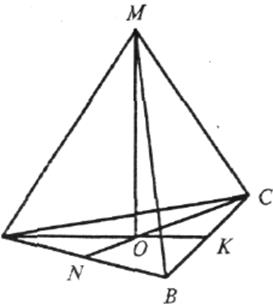
За властивістю точки перетину медіан маємо:
АО : ОК = 2 : 1, тому АО = 4 см.
Із ![]() АОМ
(
АОМ
(![]() AOM
=
90º) за теоремою Піфагора
AOM
=
90º) за теоремою Піфагора
МО = ![]() ,
,
МО = 3 см.
Відповідь. 3 см.
Точка однаково віддалена від усіх вершин правильного трикутника, а
відстань від неї до площини трикутника дорівнює ![]() см. Сторона трикутника дорівнює
см. Сторона трикутника дорівнює
![]() см.
Знайдіть відстань від даної точки до вершин трикутника.
см.
Знайдіть відстань від даної точки до вершин трикутника.
Нехай ABC —
правильний трикутник зі стороною ![]() см. Точка М така, що AM = ВM = CM.
см. Точка М така, що AM = ВM = CM.
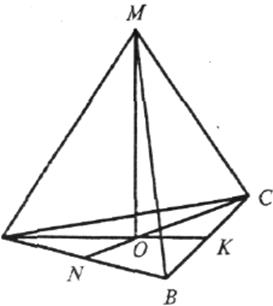
Проведемо МО![]() (АВС). Тоді MO =
(АВС). Тоді MO =![]() см, де О — центр описаного кола, АО = R — його радіус.
см, де О — центр описаного кола, АО = R — його радіус.
Як відомо,
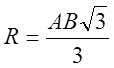
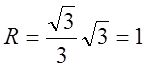 (см).
(см).
Із ![]() АОМ
(
АОМ
(![]() AOM
= 90º)
за теоремою Піфагора
AOM
= 90º)
за теоремою Піфагора
AM = ![]() ,
,
AM = ![]() =
=
![]() (см).
(см).
Відповідь: ![]() см.
см.
Картка 3.
Точка віддалена від усіх вершин прямокутного трикутника на 1см, а від
площини цього трикутника
— на ![]() см. Знайдіть медіану, проведену до
його гіпотенузи.
см. Знайдіть медіану, проведену до
його гіпотенузи.
Нехай ABC —
прямокутний трикутник, у якого ![]() С = 90º. Точка М така, що АМ = СМ = ВМ = 1 см.
С = 90º. Точка М така, що АМ = СМ = ВМ = 1 см.
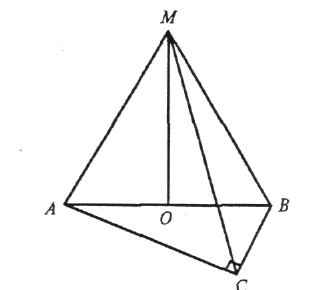
Проведемо MO![]() (ABC). Тоді МО =
(ABC). Тоді МО = ![]() см, де точка О — центр описаного навколо
см, де точка О — центр описаного навколо ![]() ABC кола, є серединою гіпотенузи і
АО = ОС = OB = R, ОС — медіана
ABC кола, є серединою гіпотенузи і
АО = ОС = OB = R, ОС — медіана ![]() АВС .
АВС .
Із ![]() АОМ
(
АОМ
(![]() AOM=
90°)
за теоремою Піфагора
AOM=
90°)
за теоремою Піфагора
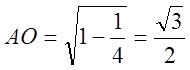 (см),
тому
(см),
тому
OC = ![]() см.
см.
Відповідь. ![]() см.
см.
3. Повторення правил проектування.
4. Розв'язування задач.
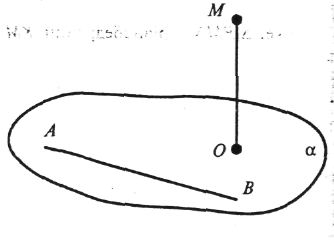
На заготовлених на дошці малюнках проведіть відрізок, що є відстанню від точки О до прямої АВ, якщо:
а)МО![]() α;
α;
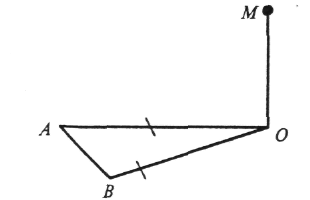
б) МО![]() (АВО), АО = ВО,
(АВО), АО = ВО,
в) МО![]() (АВС),
(АВС), ![]() CAB=90°;
CAB=90°;
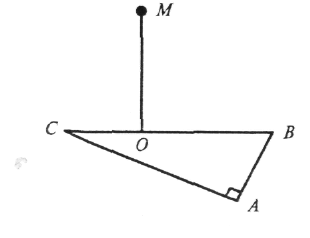
г) MO![]() (ABC), ABCD — квадрат;
(ABC), ABCD — квадрат;
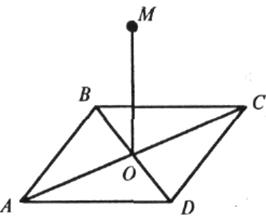
ґ) MO![]() (ABC), ABCD - ромб.
(ABC), ABCD - ромб.
А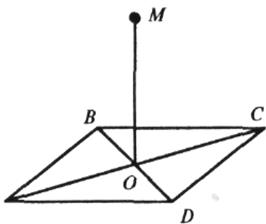
Учні розмірковують над тим, як на кожному з малюнків побудувати відрізок, що є відстанню від точки М до прямої АВ, вносять свої пропозиції.
III. Вивчення нового матеріалу.
1. Формулювання та колективне доведення першої частини теореми про три перпендикуляри.
Дано:
МО![]() α,
КО — проекція похилої KM на площину α, OK
α,
КО — проекція похилої KM на площину α, OK![]() АВ.
АВ.
Довести:
АВ![]() КМ.
М
КМ.
М
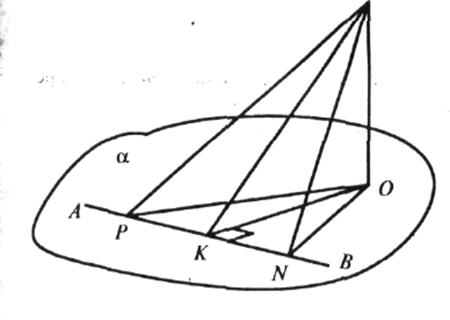
Доведення
На прямій АВ виберемо точки Р і N такі, що KN = КР.
Тоді РО = NO — як похилі до прямої АВ, що мають рівні проекції РК = =KN.
РМ = NM — як похилі до площини α , проекції яких РО і NO також рівні.
Отже, ![]() PMN— рівнобедрений, КМ — його медіана. Тому МК
PMN— рівнобедрений, КМ — його медіана. Тому МК![]() АВ
.
АВ
.
2. Формулювання та самостійне доведення твердження, оберненого до доведеного.
3. Демонстрація теореми на моделях.
IV. Розв'язування задач на закріплення теореми.
1. На кожному із малюнків а—ґ (див. п. ІІ, 4) побудуйте відрізок, що є відстанню від точки М до прямої АВ. Прокоментуйте побудову, зробіть відповідні записи.
2. Колективне розв'язування задачі.
Дано:
![]() АВС— рівнобедрений, МО
АВС— рівнобедрений, МО![]() (АВО), АВ = ВС = 17 см, МО=30см.
(АВО), АВ = ВС = 17 см, МО=30см.
Знайти: відстань від точки М до сторони А В.
3. Усне розв'язування задачі.
Дано: ![]() АВС— прямокутний,
АВС— прямокутний, ![]() С=90º, ВО = 6 см,
С=90º, ВО = 6 см, ![]() В = 30°, МО = 4 см, О є ВС.
В = 30°, МО = 4 см, О є ВС.
Знайти: відстань від точки Мдо сторони/IB.
4. Самостійне розв'язування задачі.
5. Розв'язування задачі з коментуванням.
Дано: ABCD — ромб, О — точка перетину діагоналей, МО = 4 см, BD = =6см, АС = 8см.
Знайти: відстань від точки М до сторони ромба АВ.
6. Усне розв'язування задач.
На кожному з малюнків назвіть відрізок, який є відстанню від точки М до прямої NK.
а) NBCKN1B1MK1 – куб;
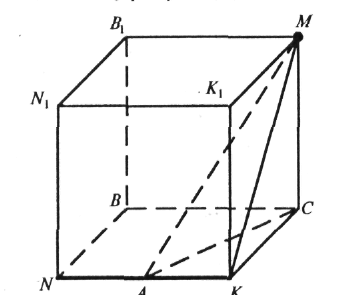
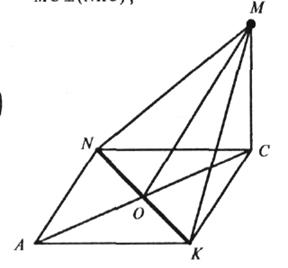
б) ANCK
– ромб, MC![]() (NKC);
(NKC);
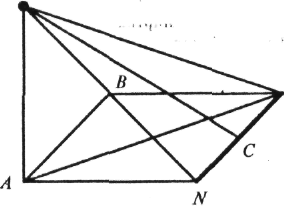
в) ABKN
—
прямокутник, AM![]() (ABK).
(ABK).
М
V. Підсумок уроку.
VI. Домашнє завдання.
1. Вивчити формулювання та доведення теореми про три перпендикуляри.
2. Розв'язати задачі № 48, 53 із § 17 підручника.
Пропоную добірку задач, які сприяють свідомому засвоєнню даної теореми. Такі задачі можна розв'язувати усно за готовими малюнками, використовувати для індивідуального контролю або для самостійної роботи. Задачі можна розглядати як підготовчі до розв'язування складніших задач.
Добірка складається з чотирьох груп задач.
1. Задачі на доведення перпендикулярності прямих.
2. Задачі на побудову перпендикуляра до прямої.
3. Задачі на побудову відрізка, що є відстанню від точки до прямої.
4. Задачі на обчислення відстані від точки до прямої.
Перша група задач І.
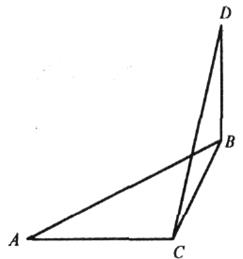
1. Дано: DB![]() (ABC),
(ABC), ![]() ВАC = 30º,
ВАC = 30º, ![]() АBC=60º.
АBC=60º.
Довести:DC![]() AC.
AC.
2. Дано: ABCD
— квадрат, MB![]() (ABC):
(ABC):
Визначте, які з трикутників прямокутні.
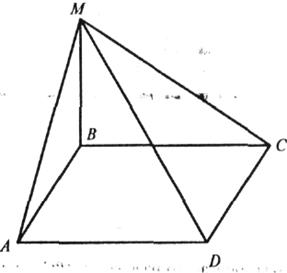
3.
Дано:
МС![]() (АВС),
АС = ВС, AD = DB.
(АВС),
АС = ВС, AD = DB.
Довести: AB![]() DM.
DM.
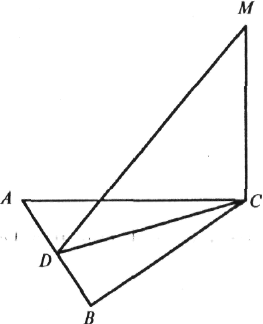
4.
Дано:
МА![]() (АВС),
BD
= CD, MD
(АВС),
BD
= CD, MD![]() CB.
CB.
Довести: АВ = АС.
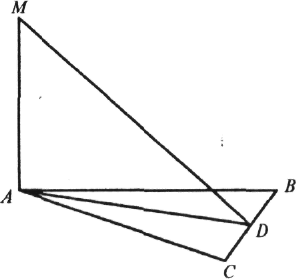
1. Із точки М опустіть перпендикуляр на сторони AD і DC та діагональ АС, якщо MK![]() (ABC)
і:
(ABC)
і:
а) АВСD — квадрат;
б) ABCD — ромб.
A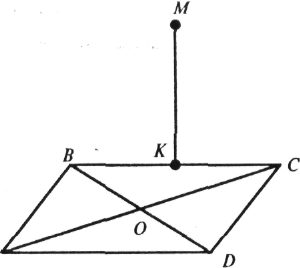
2. Із точки М опустіть перпендикуляр на діагональ АС та сторону DC, якщо MB![]() (ABC)
і:
(ABC)
і:
а) ABCD – ромб;
б) ABCD — прямокутник.
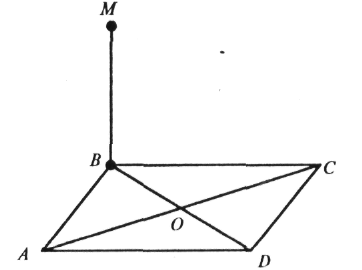
3. Із точки М опустіть перпендикуляр на сторону ВС, якщо МО![]() (АВС)
і: . a) ABCD — ромб;
(АВС)
і: . a) ABCD — ромб;
б) ABCD — квадрат.
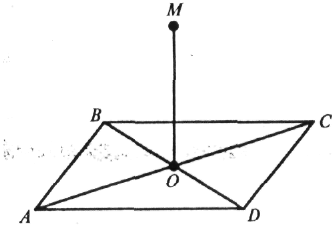
4. Із точки М опустіть перпендикуляр на сторони АС і ВС, якщо MO![]() (ABC)
і:
(ABC)
і:
а) ![]() С = 90º;
С = 90º;
б) АВ = ВС.
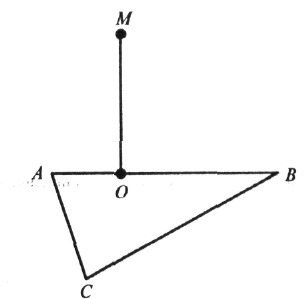
5. Із точки М опустіть перпендикуляр на сторону AD, якщо ABCD — трапеція, у якої ВС || AD і:
а) ![]() А
= 90º;
А
= 90º;
б) АВ = CD.
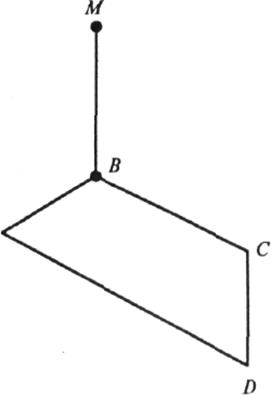
6. Із точки М опустіть перпендикуляр на сторону AD, якщо ABCD — ромб, MC![]() (ABC),
(ABC), ![]() C=30º.
C=30º.
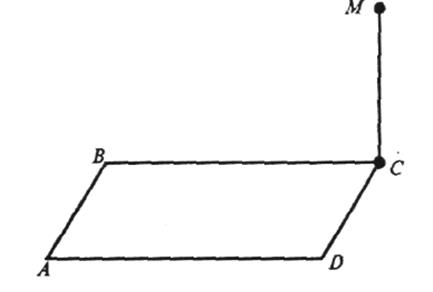
7. Із точки М опустіть перпендикуляр на сторону АВ, якщо ![]() ABC,
ABC, ![]() В = =120º, МС
В = =120º, МС![]() (АВО).
(АВО).
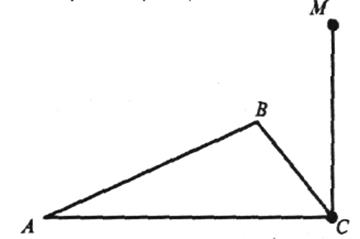
Третя група задач
1. На кожному з малюнків назвіть відрізок, що є відстанню від точки М простору до прямої AD.
а) ABCDA1B1MD1 — куб;
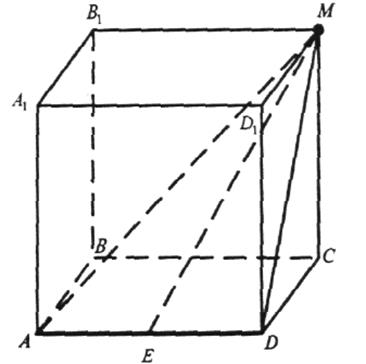
б) AВCD
—
прямокутник, CM![]() (ABC);
(ABC);
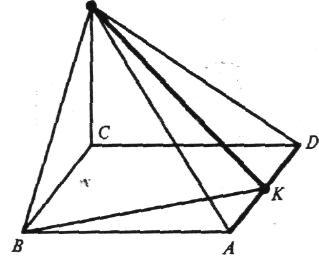
в) ABCD
— квадрат
(ромб), MC![]() (ABC)
(ABC)
Четверта група задач
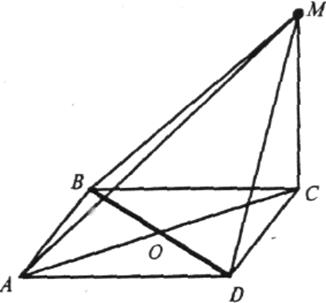
1. Знайдіть відстані від точки М до вершин, сторін і площини многокутника та площу многокутника, якщо:
а) ![]() АВС—
рівносторонній, АВ =
ВС = АС = а, О— центр
АВС—
рівносторонній, АВ =
ВС = АС = а, О— центр ![]() АВС, MO
АВС, MO![]() (ABC), пряма МС утворює з
площиною
(ABC), пряма МС утворює з
площиною ![]() ABC кут 30º;
ABC кут 30º;
М
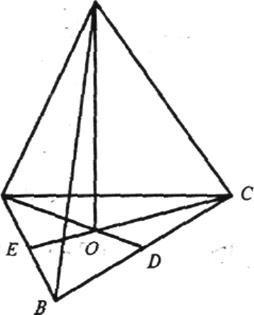
б) ABCD — квадрат зі стороною а, МА = b;
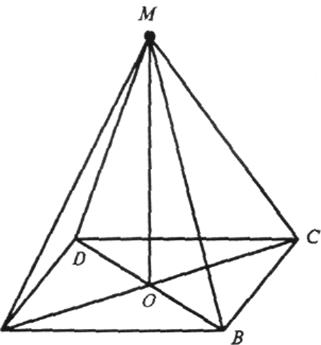
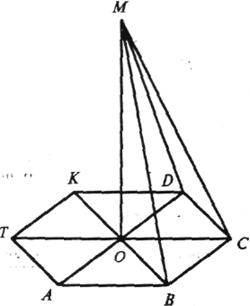
в) ABCDKT — правильний шестикутник зі стороною а, МО = b.
Література:
1. Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10— 11 кл. серед, шк. — К.: Освіта, 2000. — 128с.
2. Хроленко Н.Ф. Теорема про три перпендикуляри//Математика.–2001.–№43.–С.6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.