Площа трикутника: План-конспект уроку математики

Полтавський державний педагогічний

університет ім. В. Г.Короленка

Кафедра педагогіки

План-конспект уроку.

Підготував студент

групи М-42

фізико-математичного

факультету

ПДПУ ім. В. Г. Короленка

Демидченко Юрій Володимирович.

Методист педагогічної   практики

Кириченко С.І.

Полтава – 2004.

Тема уроку: Площа трикутника. Розв’язування задач.

Мета уроку:

Формувати практичні навички розв’язування задач з даної теми. Розкрити особливості різних видів розв’язування задач, перевірити ступінь оволодіння вивченого матеріалу.

Розвивати логічне мислення учнів, вміння виділяти основне, вміння аналізувати задачі.

Виховати культуру математичної мови, акуратність при записах на дошці та в зошиті.

Обладнання: дошка, крейда, підручники, додаткова література.

Тип уроку: комбінований.

План проведення уроку.

1. Організаційний момент.   -2хв.

2. Актуалізація опорних знань.

     Перевірка домашнього завдання.  –10хв.

3. Розв”язування задач .  -18хв.

4. Самостійна робота.  –10хв.

5. Підсумок уроку.  –3хв.

6. Домашнє завдання.  –2хв.

Хід уроку.

1.Організаційний момент.

2.Актуалізація опорних знань. Перевірка домашнього завдання.

Вчитель запитує в учнів основні формули площ трикутника. Один учень записує формули на дошці,  інші діти відповідають з місця.

Вчитель задає задачі усно для перевірки знань учнів.

1.  Знайти площу трикутника, якщо одна з сторін 7t см , а висота, проведена до неї, 4t см.

            Відповідь: 14t см.

2.  Знайти площу прямокутного трикутника з катетами 8 см і 3 см.

3.  Знайдіть площу трикутника, зі сторонами 5 і 8 см. та кутом між ними 30⁰.

        Відповідь: 10 см.

4.(письмово) Дано трикутник АВС з стороною АС=4 см і висотою ВD=2 см. Знайти площу трикутника і побудувати інший трикутник з тією ж основою АС, рівновеликий даному. Скільки таких трикутників існує?

       Відповідь: 4 см. Безліч трикутників існує.

4.  Розв”язування задач.

№24. Чому дорівнюють катети прямокутного трикутника, якщо гіпотенуза рівна 73 см, а площа дорівнює 1320 см?

Відповідь: 55 см, 48 см.

№25. У трикутнику АВС: АС=а, ВС=b. При якому куті С площа трикутника найбільша?

        Відповідь: C=90.

№31. Сторони трикутника а, b, c. Знайдіть висоту трикутника, опущену на сторону с.

             Відповідь: .

     №42. Виведіть такі формули для радіусів описаного (R) і вписаного (r) кіл трикутника:

R=, r=,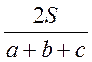

де а, b,c- сторони трикутника, а S- його площа.

Розв’язання:

Почнемо з формули для R. Як ми знаємо, R=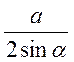, де -кут, протилежний стороні а трикутника.

     Помноживши чисельник і знаменник правої частини на bc і взявши до уваги, що bcsin=S, дістанемо:

R=.

                                              B                                                   

 

                                  c                            a

                

                                              O                                                                                                                                                                                                                

 

                             A                   b                          C      

Виведемо формулу для r. Площа трикутника АВС дорівнює сумі площ трикутників ОАВ, ОВС, ОСА:

                   S=cr+ar+br.

Звідси

r=.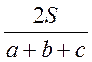

 

№43. Знайдіть радіуси описаного ( R) і вписаного (r) кіл для трикутника із сторонами: 15, 13, 4.

        Відповідь: R=, r=1,5.

   №46. Знайдіть радіус r вписаного і радіус R описаного кіл для рівнобедреного трикутника з основою 10 см і бічною стороною

 13 см.

        Відповідь:  R=  см, r= см.

5.  Самостійна робота.

1 варіант.

1. Знайти площу прямокутного трикутника, якщо його гіпотенуза с,    а один із гострих кутів .

           Відповідь:   с sin2.

    2.Знайдіть найменшу висоту трикутника із сторонами 17 см, 65 см,         

        80 см.

                Відповідь:   7,2 см.

2 варіант.

1.Визначити площу прямокутного трикутника, якщо  один із його 

катетів b, а прилеглий до нього гострий кут .

                Відповідь:   btg.

   2.Знайдіть найбільшу висоту трикутника із сторонами  см,   см,

        6 см.

              Відповідь:    4,8 см.

6.  Домашнє завдання.

Повторити пункт 124, 125. №33, №34.

          

  №33. Периметр рівнобедреного трикутника дорівнює 64 см, а його бічна сторона на 11 см більша від основи. Знайдіть  висоту трикутника, опущену на бічну сторону.

Розв”язання:

Нехай х- основа, а х+11 –бічна сторона.

           64=х+х+11+х+11;

           64=3х+22;

            х=14 (см).

S==168 (см).

  З відомої формули  S=ha слідує:

             h=13,44 см.

              Відповідь:    13,44 см.

№34. Знайдіть  висоту трикутника, у якого сторони дорівнюють 13, 14, 15 см.

Розв”язання:

За формулою Герона  S=84 см.

  З формули  S=ha знайдемо висоту h.

Висота, опущена на сторону 13 см, h=` см.

Висота, опущена на сторону 14 см, h=12 см.

Висота, опущена на сторону 15 см, h=11,2 см.

                        Відповідь: 12 см, 11,2 см,  см.