Розв'язування систем тригонометричних рівнянь: План-конспект уроку математики

Міністерство освіти і науки України

Полтавський державний педагогічний університет

Ім. В.Г.Короленка

Кафедра математики

План-конспект уроку

на тему:

’’Розв¢язування систем тригонометричних рівнянь.”

Виконав студент

Фізико-математичнлго факультету

групи Ф-51

Яценко Ігор Олексійович

Полтава 2005

Тема:роз¢язування систем тригонометричних рівнянь.

Мета:

а) навчальна: Познайомити учнів з окремими прийомами розв’язування систем тригонометричних рівнянь.

б) розвиваюча: розвинути уяву та логічне мислення у дітей, підвищити рівень їхнього інтелекту.

в) виховна: виховати інтерес до предмету, усвідомлення важливості математики у повсякденному житті.

Тип уроку: комбінований.

Обладнання:Таблиця “Тригонометрія.”

План.

1.Організаційна частина. (2хв)

2.Актуалізація опорних понять.(5хв)

3.Повідомлення нового матеріалу.(20хв)

4.Закріплення нового матеріалу.(15хв)

5.Підведення підсумків.Домашнє завдання.(3хв)

Хід уроку.

1.Організаційна частина.

Розкриваю тему та мету уроку.

2.Актуалізація опорних понять.

Для того щоб розглянути нову тему пропоную розв¢язати учням систему алгебраїчних рівнянь: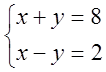

Відповідь: (5;3)

3.Повідомлення нового матеріалу.

Основні методи розв¢язування систем трегонометричних рівнянь майже такі, як і методи розв¢язування алгебраїчних систем.

Розглянемо приклади:

№1 Розв¢язати систему рівнянь

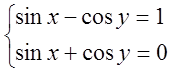
Розв¢язання.

Додавши і віднявши рівняння, одержуємо

                        

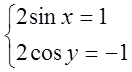
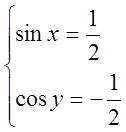
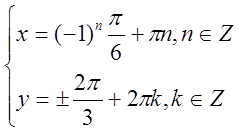
Відповідь: x=(-1)ⁿ 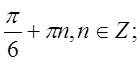  y=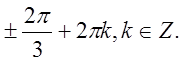

№2 Розв¢язати систему рівнянь

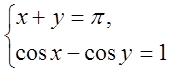
Розв¢язання.

З першого рівняння знаходимо y=π-x. Тоді

cos x-cos(π-x)=1,

cos x+ cos x=1,

2 cos x=1

cos x=

x=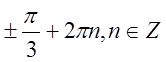

y=π-(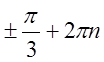)=+(1-2n)π, n є Z

Відповідь: x=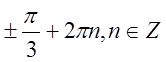; y=+(1-2n)π, n є Z.

№3 Розв¢язати систему рівнянь

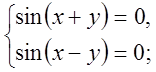
Розв¢язання.

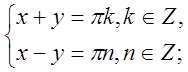
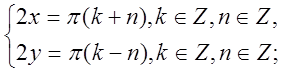
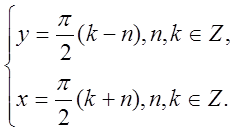
Відповідь: x=(k+n), y=(k-n), де n, k є Z.

4.Закріплення нового матеріалу.

На дошці записані завдання і запропоновано учням їх розв¢язати самостійно в зошитах. В цей час допомогаю тим хто не може в ындивыдуальному порядку.

Розв¢язати систему рівнянь

а)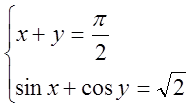

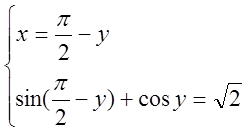
Розв¢язання

З другого рівняння sin(-y)+cos y=, маємо

cos y+ cos y=

2 cos y=

 cos y=

y₁=+2πk           y₂=-+2πk, k є Z.

x₁=-+2πk        x₂=-(-)+2πk, k є Z,

x₁=+2πk            x₂=+2πk, k є Z

Відповідь: x₁=+2πk,     y₁=+2πk

                  x₂=+2πk,     y₂=-+2πk, k є Z.

б) ;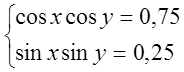

Розв¢язання.

Віднімемо нижнє рівняння від верхнього і додамо їх.

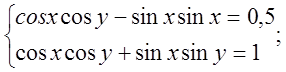
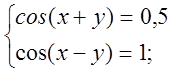
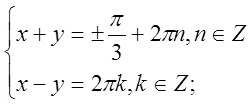
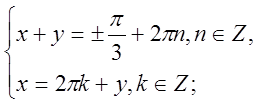
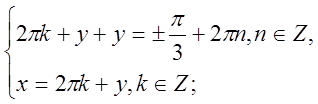
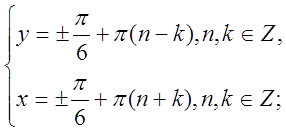
Відповідь: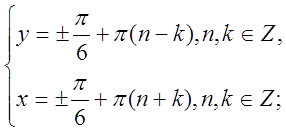

Підсумки:

Отже, сьогодні ви дізналися більше про тригонометричні рівняння, навчившись розв¢язувати системи тригонометричних рівнянь.Ви побачили, хто вміє гарно розв¢язувати рівняння, той може розв¢язувати і системи рівнянь. Отже, додому

Домашнє завдання:

Повторити тригонометричні рівняння. А також розглянути параграф розв¢язування тригонометричних систем.

 Також, дітям було задано систему рівнянь:

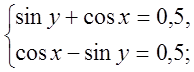
Розв¢язання.

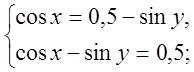
Підставимо перше рівняння в друге:

0,5-siny- siny=0,5

-2 siny=0

y=πn, n є Z

x=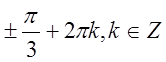

Відповідь: x=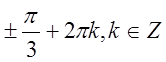; y=πn, n є Z