Правила знаходження первісних: План-конспект уроку з алгебри

План – конспект уроку з алгебри

Школа №3 м. Полтава.

Клас 11-Б.

Дата проведення уроку: 7 грудня 2004.

Підготував Геращенко Дмитро Миколайович.

Урок викладу нового матеріалу.

Тема: Правила знаходження первісних

Мета:

Начальна: 1) вивчити три основні правила знаходження первісних;

 2) закріпити їх розв’язуванням вправ на знаходження первісних;

 3) показати практичне значення розуміння і використання правил розв’язуванням задач фізичного змісту;

Виховна:  виховувати уважність учнів, строгість і логічну послідовність

міркувань;

Розвиваюча: розвивати вміння учнів давати математичне і фізичне

обгрунтування при розв’язуванні вправ.

Обладнання: таблиця первісних, підручники.

План уроку

1.  Актуалізація попередні хзнань учнів (3-5 хв.).

2.  Формулювання і доведення трьох основних правил знаходження первісних (10-15 хв.).

3.  Розв’язування вправ на знаходження первісних (15хв.).

4.  Розв’язування прикланих задач фізичного змісту (10 хв.).

5.  Домашнє завдання.

Хід уроку

1.  Актуалізація попередніх знань учнів.

На минулому уроці нами було з’ясовано, що називається первісною, який її зміст. Давайте пригадаємо з вами:

1)  Яка функція називається первісною?

2)  Яка залежність між функцією і її первісною?

3)  Якщо функція має первісну, то чи єдина вона? Чому?

Ми також вивели первісні деяких функцій, які записали у вигляді отакої (показати таблицю первісних) таблиці.

Але при роз’язуванні вправ і задач фізичного змісту приходиться мати справу зі складними функціями. Звісно всі їх помістити в одну таблицю неможливо, але є три основні правила, які допомагають у знаходженні первісних складних функцій.

2.  Формулювання і доведення трьох основних правил знаходження первісних.

Аналогія: при вивченні правил диференціюваня ми розглянули правила похідної суми, винесення коефіцієнта та похідної складеної функції (пригадати їх з допомогою класу). Тут діємо аналогічно!

Правило №1: Якщо функція  є первісною для функції , функція  - похідною для  то функція + є первісною для функції +.

(Первісна суми дорівнює сумі первісних).

Математично це правило записується так:

=, =         (+)=+.

                                     Дано                                    Довести

Доведення

Починаємо з того, що треба довести:

(+)=[правила диференціювання вже відомі]= +=[використовуємо те, що дано]= +, що й треба було довести.

Правило №2: Якщо функція  є первісною для функції ,  - стале число, то функція  є первісною для функції .

 (Коефіціієнт можна виносити за дужки).

Математично це правило записується так:

=, =const         ()=.

                                     Дано                                    Довести

Доведення

По аналогічній схемі.

()=[правило диференціювання відоме]==[використовуємо, що дано]= , що й треба було довести.

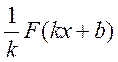Правило №3: Якщо функція  є первісною для функції ,  і  - сталі числа,  , то функція  є первісною для функції .

(Первісна складеної функції).

Математично це правило записується так:

=, ,=cons,          ()=

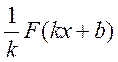          Дано                                    Довести

Доведення

По аналогічній схемі.

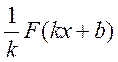()=[правила диференціювання відомі]= 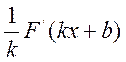==, що й треба було довести.

При доведенні правил користуватися допомогою класу!!!

3.  Розв’язування вправ на знаходження первісних.

Вимоги: розв’язати вправи на застосування сформульованих правил. При цьому:

а) звернути увагу на застосування саме певного правила;

б) користуватися таблицею первісних;

в) користуватися підтримкою учнів.

№1

Розв’язання

Використовуючи правило суми (первісна суми дорівнює сумі первісних) і таблицю первісних, маємо:

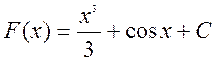. Зробіть перевірку самостійно!

№2

 

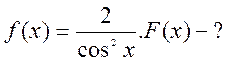
Розв’язання

Використовуючи правило винесення коефіцієнта і таблицю первісних, маємо:

, тому . Зробіть перевірку самостійно!

№3

Розв’язання

Використовуючи правило знаходження  первісної складеної функції і таблицю первісних, маємо:

, тому 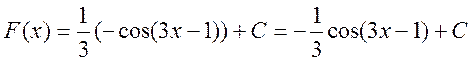. Зробіть перевірку самостійно!

4.  Розв’язування прикланих задач фізичного змісту.

План розв’язування

1)  записати математичну залежність між фізичними величинами;

2)  знайти первісні, використовуючи правила знаходження;

3)  використати початкові умови для знаходження конкретного вигляду первісних;

4)  записати рівняння зі знайденим значенням С.

Необхідно пригадати з курсу фізики залежності . Яка з даних величин є первісною?

Задача (вправа №5 підручника 1, ст. 375)

Швидкістьь руху точки задаєтьься рівнянням  (м/с). Знайти рівняння руху , якщо  (м).

Розв’язання

1) ,

2) ,

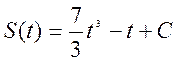3),

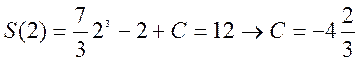4) .

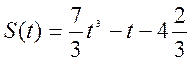Відповідь: .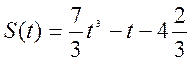

За аналогічною схемою розв’язати вправу №7 підручника 1, ст.375.

5.Домашнє завдання.

Вправи №3 (2,4,6,8), №8 (використати обидві рівності почерзі ).

Використана література

1.  М. І. Шкіль, З. І. Слєпкань, О. С. Дубинчук. Алгебра і початки аналізу. 10-11 кл. – К: Зодіак-ЕКО, 1995. Ст. 347-348, 375.

2.  З. І. Слєскань. Методика навчання математики. – К.: Зодіак-ЕКО, 2000. Ст. 418-420.