Конус. Зрізаний конус: План-конспект уроку геометрії

Міністерство освіти і науки України

Полтавський державний педагогічний університет

ім. В. Г. Короленка

Кафедра педагогіки

Конспект уроку на тему:

„Конус. Зрізаний конус”

Розробила

студентка групи М-53

фізико-математичного

факультету

Совгиря Марина Олександрівна

Полтава-2008

Тема уроку:  Конус. Зрізаний конус.

Мета уроку:навчальна: ввести означення конуса і пов’язаних з ним понять (твірна, основа конуса, радіус, висота і вісь конуса). Навчити будувати основні перерізи конуса площинами. Вчити використовувати набуті знання при розв’язуванні задач.

                      розвиваюча: розвивати логічне мислення та уяву учнів.

 виховна: виховувати культуру записів і самостійність учнів.

Тип уроку: урок подання нового матеріалу.

Обладнання на уроці: модель конуса.

Структура уроку: 1. Організаційний момент;

                                 2. Вивчення нового матеріалу;

                                 3. Розв’язування вправ;

                                 4. Підсумок уроку;

                                 5. Домашнє завдання.

ХІД УРОКУ.

1.  Організаційний момент.

2.  Вивчення нового матеріалу.

На попередніх уроках ми розглянули одне з тіл обертання – циліндр. Тож скажіть, що таке циліндр? (це тіло, утворене обертанням прямокутника навколо його сторони). Сьогодні на уроці ми познайомимося ще з одним тілом обертання, а саме – конусом. Якщо взяти прямокутний трикутник і обертати навколо одного з катетів, то утворене тіло і буде називатися прямим круговим циліндром.

Def: конусом називається тіло, утворене обертанням прямокутного трикутника навколо його катета.

                         SКатет ОА опише круг, що називається                                  

                                                                   основою конуса. Гіпотенуза SА описує бічну

                                                                   поверхню конуса (мал.1).

                                                                   l² = R² + h²;

                                                                   S_б.к.= πRl;   

                                                                   S_п.к.= πR(R + l);

                              h

                                        l

                                   

                             О

                                   R      А               мал.1

т.S називається вершиною конуса;

SO – висота конуса;

Пряма, що містить висоту конуса називається віссю конуса.

Відрізок, що сполучає вершину конуса з будь-якою точкою кола основи називається твірною конуса.

Бічна поверхня конуса складається з твірних.

Повна поверхня конуса складається з площі основи і площі бічної поверхні конуса.

Перерізи конуса площиною.

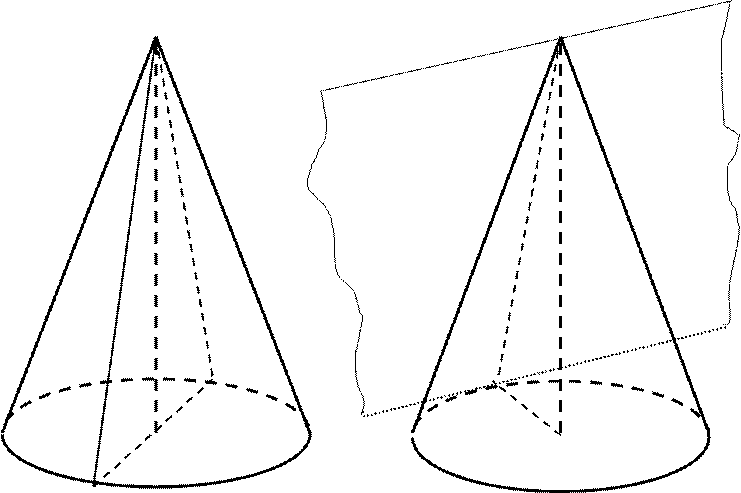                     S                                                      S

                                                   a

                               B                                  B

                       O                                                       O

         A

    Осьовий переріз                                  Дотична площина

Січна площина, паралельна основі конуса, перетинає його по кругу. Вона ділить конус на два тіла обертання: гомотетичний конус і зрізаний конус. Зрізаний конус утворений обертанням прямокутної трапеції навколо меншої бічної сторони.

                                                                                 S_б.з.к.= πl(R₁+ R₂).

 

           

Учні самостійно вдома зображують перерізи конуса площиною:

1)  яка не паралельна основі конуса, але перетинає всі його твірні;

2)  яка перетинає основу конуса і паралельна одній з його твірних.

3.  Розв’язування вправ.

Задачі № 813; 814; 816 учні розв’язують усно.

Задача 824.

Висота конуса 4, твірна 5. Знайдіть кут сектора, який є розгорткою бічної поверхні цього конуса.

Розв’язання: радіус основи конуса ОА=3. Тому довжина кола його основи

                    P                        С = 6π. Така сама довжина дуги сектора, який є

                                                розгорткою бічної поверхні конуса. Ця довжина

                                                в стільки разів менша за довжину кола радіуса

                                                РА = 5, у скільки разів шуканий кут сектора  

                                                менший від 360⁰. Отже, φ/360⁰ = 6π/10π, звідси

                                                φ = 216⁰.

                               O

                                 A

Відповідь: 216⁰.

Задача 830.

Виведіть формулу для обчислення площі бічної поверхні зрізаного конуса.

Розв’язання: якщо радіуси основ зрізаного конуса ОА = R₁ , О₁В = R₂, а твірна АВ = l, то площа його бічної поверхні дорівнює різниці площ бічних поверхонь конусів з твірними РА і РВ. Позначимо: РВ = х, тоді РА = х + l. З подібності трикутників PBO₁ і PAO маємо:

                                                      x/R₂ = (x + l)/R₁,                                                                                                                    

                    О₁        R₂                                 x = R₂l/(R₁ – R₂).       

                                    В                Отже, S = πR₁(x + l) – πR₂x = πl(R₁+ R₂).

                                                         

 

 

                                                           l

 

 

 

 

                                 O

                            R₁

                                                                А

4.  Підсумок уроку.

Сьогодні на уроці ми познайомилися ще з одним тілом обертання – конусом. На малюнку зображено конус. Назвіть відповідні елементи конуса.

                          S                                         SO - ?

                                                                     SA - ?

                                                                     SAB - ?

                                                                     т.S - ?

                                                                     OA; OB - ?

                                              B

                               O

      A