Клас: 6-а
Тема.” Коло. Довжина кола.”
Мета: Вивести поняття кола. Відкрити формулу для обчислення довжини кола, навчити користуватися цією формулою для розв’язування задач і вправ.
Тип уроку: Урок вивчення нового матеріалу.
План уроку.
1. Організаційний момент.
2. Актуалізація опорних знань.
3. Виклад нового матеріалу.
4. Розв’язування задач.
5. Домашнє завдання.
Хід уроку:
1. Організаційний момент.
2. Актуалізація опорних знань.
На дошці будують довільну пряму, промінь, відрізок.
Фронтальне опитування: Які фігури зображені на дошці?
Як їх позначають? Дайте означення прямої, променя, відрізка?
3. Виклад нового матеріалу.
Нагадати з якими фігурами учні знайомі (трикутник, чотирикутник, трапеція, паралелограм). У житті часто зустрічаються круглі фігури, наприклад, колесо велосипеда, кермо автомобіля, тарілка і т. д. А які ви знаєте круглі предмети? Ознайомимося з колом. Візьмемо циркуль. Його дві ніжки розхиляються на будь-який кут. Одна ніжка має вістря гостре, а інша – грифель. Беремо будь-який розхил циркуля і ніжку з вістрям ставимо у будь-яку точку. Позначимо цю точку О.
Інша ніжка з грифелем – рухається, а перша – ні. Зазначимо грифелем кілька точок. Розхил циркуля не змінювали, тобто всюди він один і той самий: і та, й інша точки – всі розміщені на однаковій
відстані від т.О, а тому ці точки називаються рівновіддаленими від т.О. ми можемо грифелем наставити цих точок дуже багато, одна біля одної, так, що всі вони утворять замкнену лінію. Таку лінію і називають колом, а точку О – центром кола. Усі точки, що утворюють коло, називаються точками кола. Візьмемо і з’єднаємо т.О з будь-якою точкою кола, наприклад з точкою А. Отримаємо відрізок ОА. Відстань від т.О до точки кола називається радіусом кола і позначається буквою r або R. Радіусом кола називається також відрізок, що з’єднує будь-яку точку кола з його ценром. Радіуси одного кола рівні. Намалюємо коло і проведемо через центр відрізок АВ.
Такий відрізок АВ називається діаметром кола і позначається буквою d.
Діаметр – відрізок, що сполучає дві точки кола і проходить через центр.
Подивіться уважно на малюнок.
Чим є відрізки ОА і ОВ? (радіуси).
Можемо сказати, що АВ складається з двох радіусів ОА і ОВ. АВ=АО+ОВ.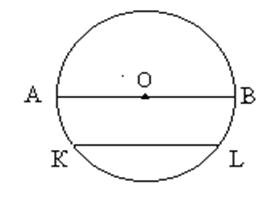
Звідси випливає, що d=r+r; d=2r. Отже, діаметр дорівнює подвоєному радіусу.
Ми розглянули діаметр – відрізок, що проходить через центр кола з кінцями на колі, але ж є й такі відрізки, що не проходять через центр кола. Відрізок, що з’єднує будь-які дві точки кола, називається хордою. KL – хорда. Найбільша хорда є його діаметр.
Літерою С позначають довжину кола, а d – діаметр. Архімед після довгих вимірювань помітив, що якщо точно виміряти ці величини і знайти відношення довжини кола до його діаметра, то в усіх випадках він отримував 3,14. Простіше виміряти діаметр кола і помножити на 3,14. Відношення С/d домовилися позначати π і тому формулу обчислення довжини кола записують так: C=πd або C=2πr оскільки d=2r π= C/d.
4. Розв’язування задач.
№ 905 (усно).
Знайдіть довжину кола діаметром 10см.
d=10см.
π=3,14
С – ?
Розв’язання:
С=πd; С=10*3,14=31,4(см)
Відповідь: С=31,4см.
№ 907 (усно).
Знайдіть довжину кола радіуса 5дм.
r=5дм
π=3,14
С – ?
Розв’язання:
С=2πr; С=2*3,14*5=31,4(дм).
Відповідь: 31,4дм.
№ 911.
Довжина кола дорівнює 11м. Знайдіть діаметр.(π=22/7).
С=11м.
π=22/7
Розв’язання:
С=πd, d=С/π; 11/3,14=3,5(м).
Відповідь:d=3,5м.
5. Завдання додому:
§6 № 907, 913.
№ 907.
Знайдіть довжину кола а) діаметра: 2,5см.
в) радіуса: 5см.
а) d=2,5см.
С-?
Розв’язання:
С=πd; С=2,5*3,14=7,85(см),
в) r=5см
С-?
Розв’язання:
С=2πr; С=2*3,14*5=31,4(см).
Відповідь: 7,85(см); 31,4(см).
№913.
Який шлях подолає в пустелі верблюд, пройшовши по колу радіуса 3 км?
r=3км
π=3,14
Розв’язання:
С=2πr; С=2*3,14*3=18,84(км).
Відповідь: С=18,84км.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.