Задание расчёта
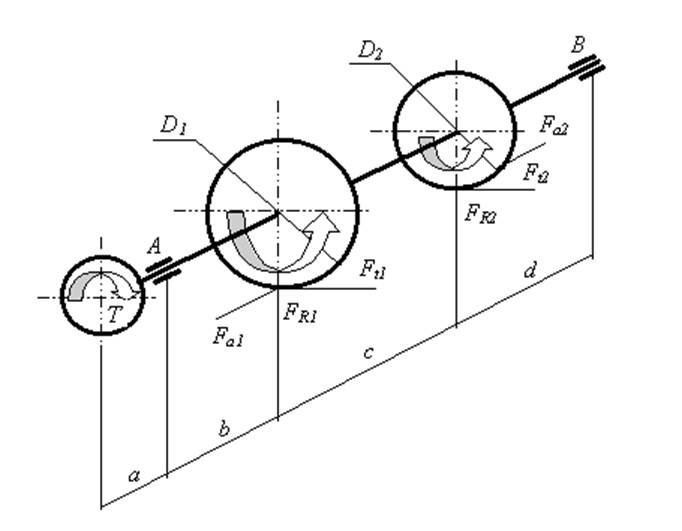 |
параметров (таб.1).
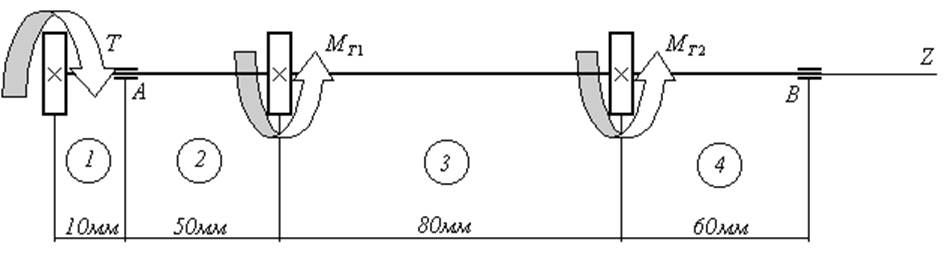
Рис.1. Расчётная схема вала
Таблица 1. Значения заданных параметров.
|
№ |
Наименование |
Обозначение |
Значение |
|
1 |
Окружная сила, Н |
FT1 |
200 |
|
2 |
Окружная сила, Н |
FT2 |
100 |
|
3 |
Продольная сила, Н |
FA1 |
54 |
|
4 |
Продольная сила, Н |
FA2 |
27 |
|
5 |
Радиальная сила, Н |
FR1 |
73 |
|
6 |
Радиальная сила, Н |
FR2 |
36 |
|
7 |
Крутящий момент ведущего колеса, Нмм |
T |
1,45*104 |
|
8 |
Диаметр ведомого колеса, мм |
D1 |
120 |
|
9 |
Диаметр ведомого колеса, мм |
D2 |
50 |
|
10 |
Размеры расчетных участков, мм |
a b c d |
10 50 80 60 |
|
11 |
Материал |
Ст.50 |
|
1. Теоретическое введение
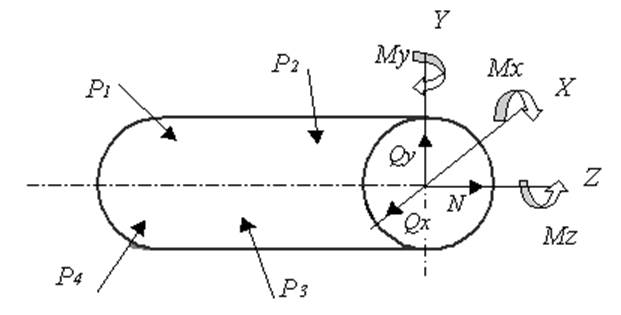 |
Рис.2.
Для составления уравнений, характеризующих внутренние силовые факторы, необходимо провести исследование по отдельным участкам стержня, предварительно выбрав систему координатных осей. Удобнее всего оси выбрать так, чтобы одна из них совпадала с осью стержня, а две других были в плоскости поперечного сечения. Продольную ось стержня обозначим Oz. Оси Oy и Ox совместим с плоскостью поперечного сечения. Показав систему осей на одном из горизонтальных участков, переход к изображению на других осуществляем поворотом осей, сохраняя всегда правую систему (поворот оси ОХ к оси ОУ на прямой угол – при взгляде на нее с положительной оси Оz – следует проводить против часовой стрелки).
Условимся положительным считать изгибающий момент, при котором сжатое волокно обращено в сторону положительного направления данной оси (для Мх – оси Оу и т.д.). Знак для крутящего момента установим положительным, если момент направлен по часовой стрелке при взгляде на него с положительного направления оси Оz; знак поперечной силы – положительным при совпадении ее направления с положительной осью и знак N – положительным при растяжении.
Валы являются ответственными деталями всех машин. На валах и осях размещают вращающие детали: зубчатые колёса, шкивы, барабаны и т.п. Вал передаёт вращающий момент от одной детали к другой. Современный расчет валов состоит из расчета на прочность материала при переменных напряжениях с учётом концентрации напряжений и других факторов, влияющих на усталочную прочность, и проверки по упругим колебаниям и допускаемым деформациям.
Подавляющее большинство валов имеет прямую ось и две опоры. Валы с изогнутой осью (коленчатые) и многоопорные (статически неопределимые) принципиально рассчитываются так же, однако расчёт последних будет сложнее из-за наличия в валах пространственной оси и статически неопределимой конструкции.
Основные требования предъявляемые к валам, следующие: механическая прочность, жесткость, долговечность, целесообразная конструктивная форма и технологичность изготовления при минимальных затратах материала. Получить окончательные размеры вала прямым расчётом невозможно. Поэтому расчет ведётся предварительным подбором с последующей проверкой принятых размеров.
2. Расчётная часть
2.1. Составление расчетных схем
Непосредственно на вал все нагрузки передаются через ступицы закреплённых на валу деталей (зубчатые колёса, шкивы, подшипники и т. д.) в виде сил, распределённых по посадочной площади и по рабочим элементам шпонок и шлицов. При расчёте вала принимают, что нагрузки от укреплённых на нем деталей передаются на вал в виде сосредоточенных сил и моментов (рис.3,4,5). Нагрузки прикладываются против середины длины рабочего элемента детали (середины зуба или середины обода шкива), но не против середины ступицы, т. к. ступица может быть несимметрично относительно рабочих элементов детали.
Для расчёта вала составляем расчётные схемы (рис.3,4,5). Для этого все силы, приложенные к укреплённым на валу деталям, раскладываем на вертикальные горизонтальные составляющие и эти составляющие приводим к оси вала. Причём, нагрузки прикладываем так, как они по условиям задачи расположены в пространстве (рис.2).
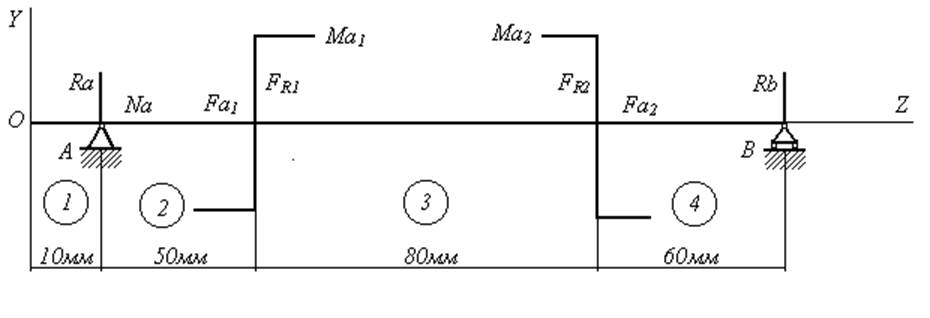 |
Рис.3. Расчетная схема продольно – вертикальной плоскости YOZ
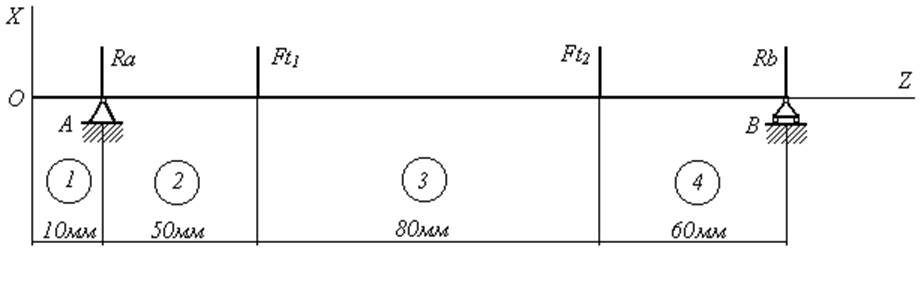 |
Рис.4. Расчетная схема горизонтальной плоскости XOZ
 |
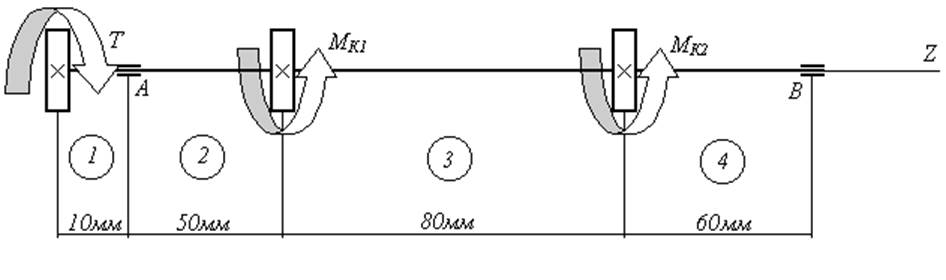 |
На расчётных схемах в вертикальной (рис.3) и горизонтальной (рис.4) плоскостях вал изображен в виде балки на двух опорах. Одну из опор балки изображаем шарнирно-неподвижной, а другую – шарнирно-подвижной.
2.2. Подбор диаметра вала по допускаемым напряжениям
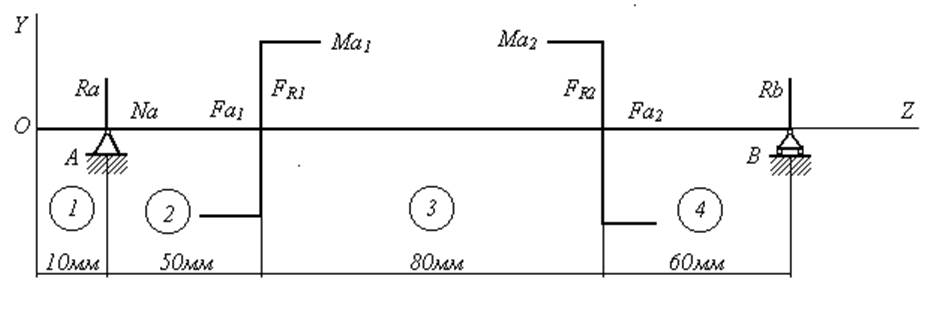 |
Рис.6. Схема нагрузок в продольно – вертикальной плоскости YOZ
![]() ;
;
![]() ;
;
![]() Н.
Н.
 , Нмм;
, Нмм; 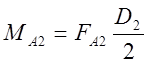 ,
Нмм.
,
Нмм.
![]() Нмм,
Нмм, ![]() Нмм.
Нмм.
![]() ;
;
![]() ;
;
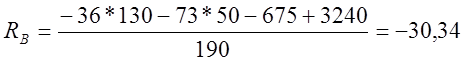 Н.
Н.
![]() ;
;
![]() ;
;
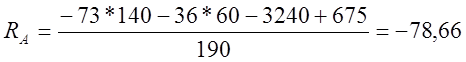 Н.
Н.
Проверка:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2.2.2. Вычисление внутренних усилий в поперечных сечениях вала
продольно – вертикальной плоскости YOZ
Для определения внутренних силовых факторов используем метод сечений. Для этого разбиваем балку на рабочие участки (рис.11).
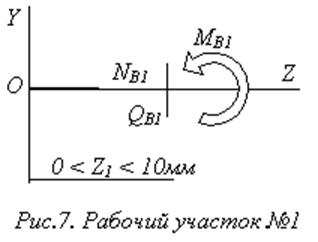
![]() Н;
Н;
![]() Н;
Н;
![]() Нмм.
Нмм.
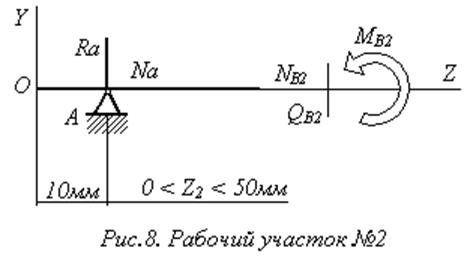
![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при ![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.

Рис.9. Рабочий участок №3
![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при ![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.

![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.
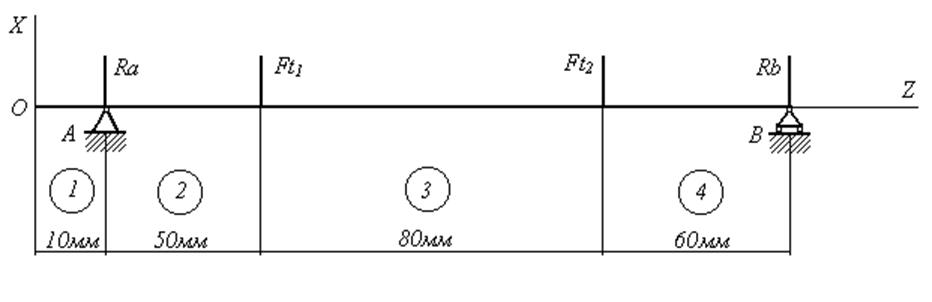 |
плоскости XOZ
Рис.12. Схема нагрузок в горизонтальной плоскости ХOZ
![]() ;
;
![]() ;
;
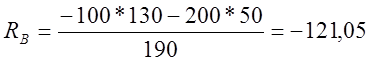 Н.
Н.
![]() ;
;
![]() ;
;
 Н.
Н.
Проверка:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2.2.4. Вычисление внутренних усилий в поперечных сечениях вала
горизонтальной плоскости XOZ
Разбиваем балку на рабочие участки (рис.17).

![]() Н;
Н;
![]() Н;
Н;
![]() Н.
Н.
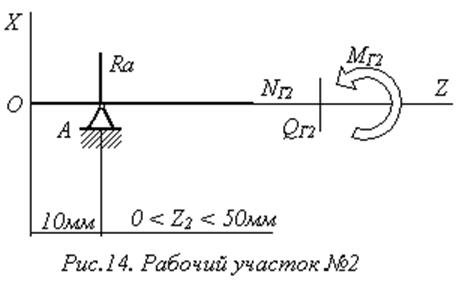
![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при ![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.
 |
![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при ![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.
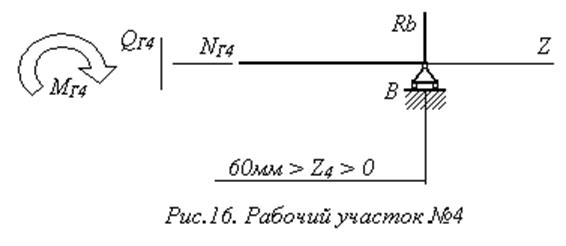
![]() Н;
Н;
![]() Н;
Н;
![]() ,
,
при ![]() мм
мм ![]() Нмм,
Нмм,
при ![]() мм
мм ![]() Нмм.
Нмм.
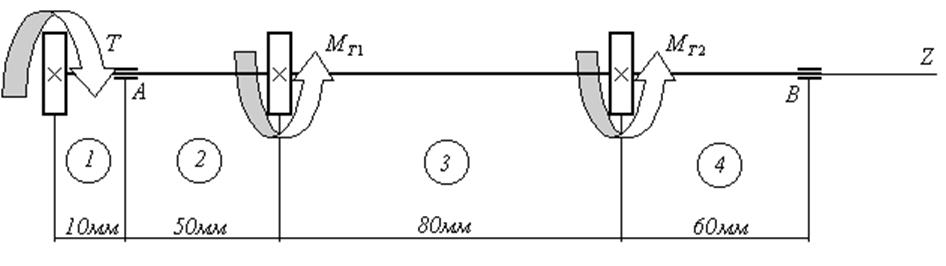 |
Рис.18. Расчётная схема крутящих моментов МК
 , Нмм;
, Нмм; 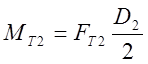 ,Нмм.
,Нмм.
![]() Нмм,
Нмм, ![]() Нмм.
Нмм.
Строим эпюру крутящих моментов МК (рис.19):
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм.
Нмм.
2.2.6. Расчёт полных изгибающих моментов М
По
нагрузкам и реакциям в вертикальной и горизонтальной плоскостях можно вычислить
усилия в любом сечении по длине вала: поперечную силу QB и QГ , изгибающий момент MB и МГ , крутящий момент МК и продольную силу N.
Геометрическим суммированием можно вычислить величину полной поперечной силы ![]() и полного изгибающего момента
и полного изгибающего момента ![]() .
.
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
![]() Нмм;
Нмм;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.