Расчет функций интегрирующего звена

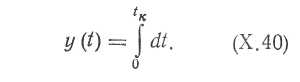
Из уравнения (Х.40) нетрудно получить переходную функцию интегрирующего звена

_Соответствующая этому случаю зависимость показана на рис. Х8 а.

Амплитудно-фазовая характеристика интегрирующего звена. Подставив в   X 39   s =jω и отделив мнимую часть от действительной, получим

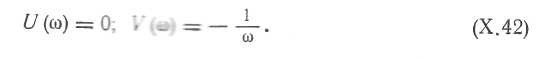
В соответствии с этим можно определить амплитудную и фазовую частотные характеристики:

Изменяя ω от 0 до ∞, получим, что конец вектора W(jω) движется по отрицательней части мнимой оси (см. рис. Х.8, б).

Логарифмическая и амплитудная и фазовая частотные характеристики интегрирующего звена. Исходя из формулы (Х.43) и  (Х.44), имеем

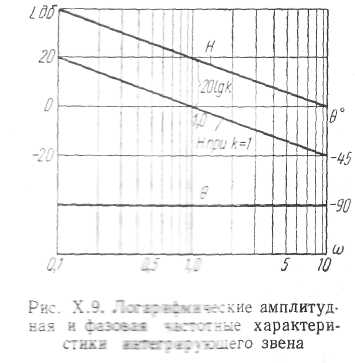
Эти  характеристики построены на рис.  Х.9.

Если имеется усилительное и интегрирующее звенья, т. е.

то логарифмическая амплитудная характеристика поднимается при ω = 1 на величину 20 lg k(см. рис. Х.9).