Министерство образования РФ
Сибирский государственный технологический университет
Кафедра АПП
Расчетно-графическая работа
Выполнил: студент гр.23-2
__________ Кирюхин П.В.
(подпись)
Проверила:
__________ Чмых Г.И.
(подпись)
Задание 1
|
 |
|
|
Уравнение динамики объекта:
![]()
Уравнение динамики регулятора:
![]()
Параметры системы имеют значения:Т1=5 с; Ко=1,5;K1=0.2,с=15,b1=2.
Статическая характеристика релейного элемента приведена на рисунке 2.
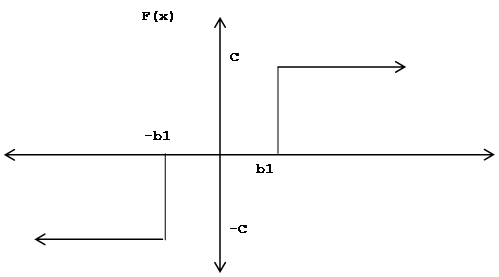
Рисунок 2 - Релейный элемент с гистерезисом и насыщением.
Задание 2
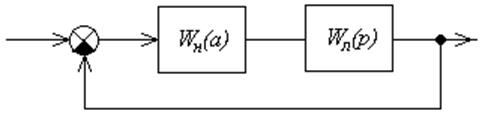 |
Рисунок 3 – Структурная схема нелинейной системы.
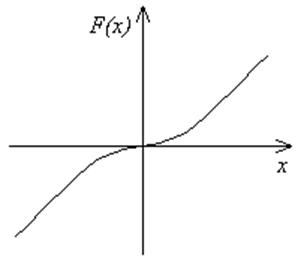 |
Рисунок 4 – Нелинейное звено.
Передаточная функция линейного
звена 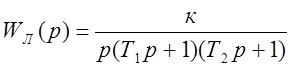 , где к=5;Т1=0,2; Т2 = 0,1.
, где к=5;Т1=0,2; Т2 = 0,1.
Содержание
Введение
1 Уравнения фазовых траекторий.
1.1 Уравнение динамики объекта регулирования
1.2 Уравнение динамики регулятора
1.3 Уравнение динамики системы
1.4 Преобразование уравнение динамики системы
1.5 Дифференциальные уравнения фазовых траекторий
1.6 Нелинейная функция заданного элемента
1.7 Дифференциальные уравнения фазовых траекторий в области 1
1.8 Дифференциальные уравнения фазовых траекторий в области 2
1.9 Дифференциальные уравнения фазовых траекторий в области 3
1.10 Расчётные формулы для фазовых траекторий
2 Построение фазовых траекторий
3 Метод гармонической линеаризации
Введение
Исследование и проектирование нелинейных систем автоматического регулирования можно вести точными и приближёнными методами.
Наибольшее применение в теории автоматического регулирования получили точные методы, основанные на рассмотрении фазовой плоскости и картины протекания переходных процессов во времени. Точные методы являются достаточно трудоёмкими и требуют значительных затрат времени.
Приближённые методы отличаются большой универсальностью и простотой. Однако имеются определённые ограничения при их применении, которые необходимо учитывать, так как в противном случае возможен неверный результат.
К приближённым методам, получившим наибольшее распространение, относятся второй метод Ляпунова, метод гармонической и статической линеаризации.
Метод фазовой плоскости применяют для анализа устойчивости процессов регулирования, описываемых нелинейными дифференциальными уравнениями второго и вырожденными уравнениями третьего порядка. Для построения траектории движения изображающей точки на фазовой плоскости нашли применение четыре способа: аналитический (решение нелинейных уравнений по участкам), изоклин, с помощью цифровых и аналоговых вычислительных машин.
1 Уравнения фазовых траекторий
1.1 Уравнение динамики объекта регулирования
|
|
(1) |
1.2 Уравнение динамики регулятора
|
|
(2) |
1.3 Уравнение динамики системы находим, продифференцировав уравнение (1) и затем подставляя в него уравнение (2)
|
|
(3) |
1.4 Представим уравнение (3) в виде:
|
|
(4) |
|
|
|
|
|
(5) |
1.5 Дифференциальное уравнение фазовых траекторий получим путём исключения времени из системы уравнений (4), (5). Для этого поделим уравнение (5) на уравнение (4)
|
|
(6) |
1.6 В соответствии с заданной характеристикой нелинейного элемента, нелинейную функцию F(x) можно описать следующим образом:
|
|
|
|
|
|
В связи с этим на фазовой плоскости (х, у) можно выделить три области: (1)F(x)=-с; (2)F(x)=с; (3)F(x)=0.
1.7 Дифференциальные уравнения фазовых траекторий в области (1)
|
|
(7) |
|
Которое после разделения переменных примет вид: |
|
|
|
Проинтегрировав уравнение (6), получим уравнение фазовых траекторий для области (1) -левой полуплоскости:
|
|
|
|
|
(8) |
где К = KiKo; Ci - произвольная постоянная интегрирования.
Из уравнения (8) видно, что при У= КС, имеем х = +∞, откуда следует, что все фазовые траектории, отвечающие различным значениям произвольной постоянной C1, имеют общую асимптоту у = КС, к которой они стремятся при х->∞.
Из выражения (7) видно, что при у = 0 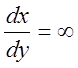 это
значит, что фазовыетраектории перпендикулярны к оси х в точках
пересечения с ней.
это
значит, что фазовыетраектории перпендикулярны к оси х в точках
пересечения с ней.
1.8 Дифференциальные уравнения фазовых траекторий в области (2)
|
|
(9) |
откуда аналогично уравнению (8), уравнение фазовых траекторий будет:
|
|
(10) |
Фазовые траектории в области (2) стремятся к асимптоте у = -КС при х->-∞
1.9 Дифференциальные уравнения фазовых траекторий в области (3)
|
|
(11) |
откуда аналогично уравнению (8), уравнение фазовых траекторий будет:
|
|
(12) |
1.10 Расчётные формулы для фазовых траекторий в соответствии с заданными значениями параметров будут иметь вид:
|
|
(13) |
|
|
(14) |
|
|
(15) |
2 Построение фазовых траекторий
Для построения фазовых траекторий на фазовой плоскости
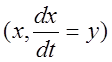 проведёмдве линии
переключении: при
проведёмдве линии
переключении: при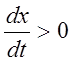 - вправо от оси ординат на расстоянии b1 ипри
- вправо от оси ординат на расстоянии b1 ипри 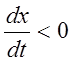 -
влево от оси ординат на расстоянии –b1. По
уравнению (13) задаваясь различными значениями постоянной интегрирования,
рассчитываем для правой полуплоскости фазовые траектории (правее b1).
-
влево от оси ординат на расстоянии –b1. По
уравнению (13) задаваясь различными значениями постоянной интегрирования,
рассчитываем для правой полуплоскости фазовые траектории (правее b1).
Пользуясь свойствами фазовых траекторий, указанными в п. 1.7 и п. 1.8 по данным расчёта строим фазовые траектории (Рисунок 5).
Для левой полуплоскости (левее -b1) фазовые траектории будут симметричны траекториям правой полуплоскости относительно начала координат.
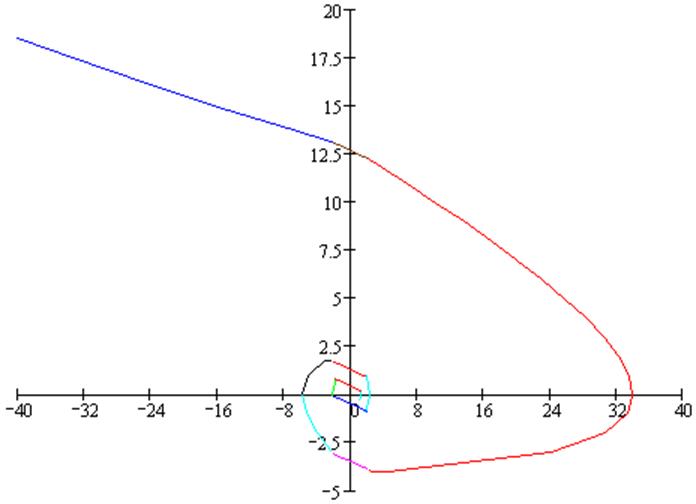 |
Рисунок 4 – Фазовая траектория.
1) Построим амплитудно-фазовую частотную характеристику линейной части системы Wл(jw) и годограф гармонически линеаризованного звена –1/Wн(ja).
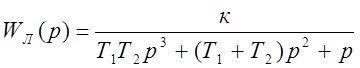 ;
;
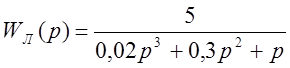 .
.
Подставляем р=jw в передаточную функцию линейной части:
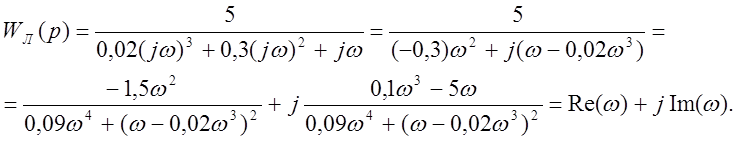
2) Годограф гармонически линеаризованного нелинейного звена определяется:
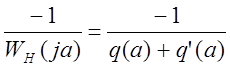 ;
;
где 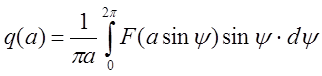 и
и
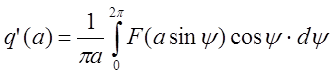 -
коэффициенты гармонической линеаризации.
-
коэффициенты гармонической линеаризации.
Для усилителя с кубической нелинейностью q’(a)=0,
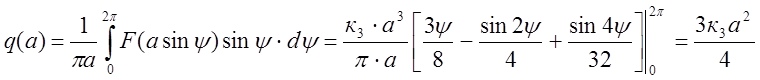 ;
;
![]() .
.
Отсюда годограф гармонически линеаризованного нелинейного звена равен:
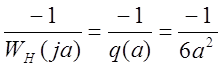
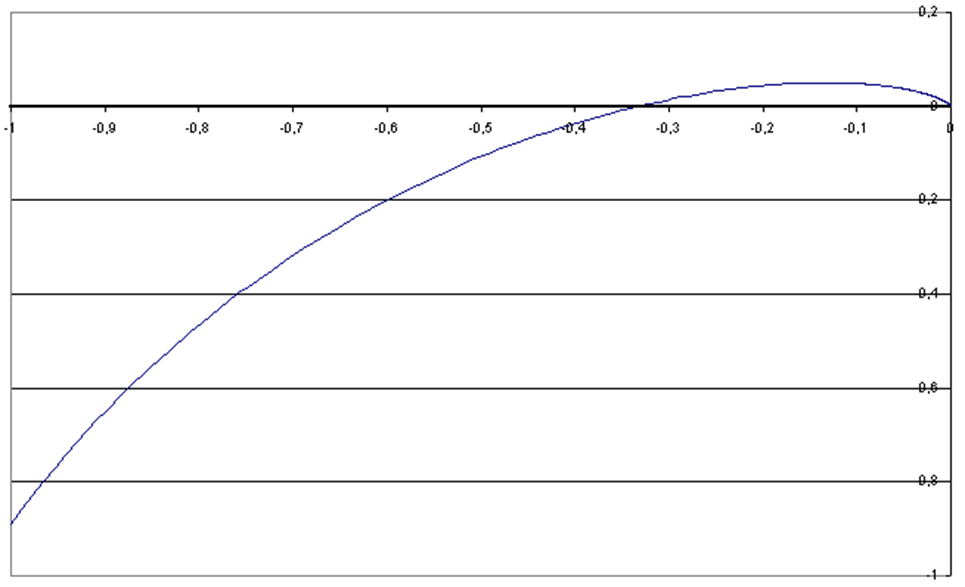
3) Строим в одной и той же системе координат амплитудно-фазовую характеристику Wл(jw) и годограф гармонически линеаризованного нелинейного звена WH(ja) – рисунок 6.
Таблица – Значения для построения АФЧХ.
|
w |
0,001 |
0,101 |
0,201 |
0,301 |
0,401 |
0,501 |
0,601 |
0,701 |
1,001 |
1,201 |
1,801 |
2,801 |
|
Re(w) |
-1,5 |
-1,4992 |
-1,4969 |
-1,4932 |
-1,488 |
-1,4814 |
-1,4733 |
-1,464 |
-1,428 |
-1,4 |
-1,286 |
-1,059 |
|
Im(w) |
-5000 |
-49,469 |
-24,805 |
-16,506 |
-12,33 |
-9,807 |
-8,1124 |
-6,893 |
-4,66 |
-3,77 |
-2,23 |
-1,062 |
|
w |
4,201 |
6,001 |
7,001 |
10,001 |
40 |
… |
300 |
400 |
588,801 |
… |
¥ |
|
Re(w) |
-0,747 |
-0,45 |
-0,34 |
-0,15 |
-0,00136 |
… |
-4,6E-07 |
-1,5E-07 |
-3,1E-08 |
… |
0 |
|
Im(w) |
-0,38 |
-0,07 |
-0,0032 |
0,05 |
0,0035 |
… |
9,24E-06 |
3,9E-06 |
1,22E-06 |
… |
0 |
 |
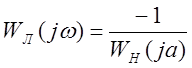 ;
;
имеет два решения
![]() ;
;
![]() ,
,
где ![]() ,
, ![]() и
и
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.