Исследование устойчивости состояния равновесия или периодических автоколебаний нелинейной системы при помощи метода гармонической линеаризации

Министерство образования Российской Федерации

Сибирский государственный  технологический

университет

 Факультет Автоматизации и информационных технологий

     Кафедра Автоматизации производственных процессов

Расчетно-графическая работа №2

(АПП.000000.005.ПЗ)

	Проверила: ____________ Чмых Г.И.          (подпись)  ____________________________                    (оценка, дата) Выполнил:  студ. гр. 23-2 ____________Захаров А.С.           (подпись)

Министерство образования Российской Федерации

Сибирский государственный  технологический

университет

  Факультет Автоматизации и информационных технологий

Учебная дисциплина: Теория управления

Задание

на курсовую работу

   Тема: «МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ»

	Руководитель:______________    (подпись)  Задание принял к исполнению ___________________________                         (подпись)

Задание

1. Исследовать устойчивость состояния равновесия или периодических автоколебаний нелинейной системы при помощи метода гармонической линеаризации при учете типа нелинейности (рисунок 2), структурная схема которой изображена на рисунке 1, где Wл(р) – передаточная функция линейной части, Wн(а) – гармонически линеаризованная передаточная функция нелинейного звена.

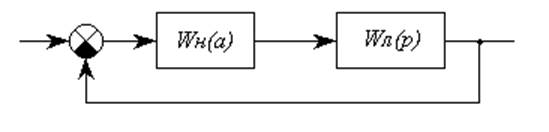Рисунок 1 - Структурная схема нелинейной системы

2. Если в системе возможны периодические колебания, то определить их частоту и амплитуду.

Передаточная функция линейной части задана уравнением:

.

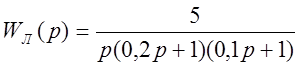Параметры нелинейного звена: С = 5.

Рисунок 2 - Идеальное реле

Реферат

В данной расчётно-графической работе представлено исследование устойчивости состояния равновесия или периодических автоколебаний нелинейной системы при помощи метода гармонической линеаризации при заданном типе нелинейности – идеальное реле, а так же расчёт частоты и амплитуды при периодическом колебании.

Расчётно-графическая работа содержит пояснительную записку из 12 страниц текста,  5  рисунков, 2 литературных источника.

Содержание

Введение ………………………………………………………………………………………………6

1 Амплитудно – фазовая частотная характеристика линейной части

системы ………………………………………………………………………………………………7

2 Амплитудно – фазовая характеристика нелинейного звена ……………………………8

3 Определение частоты и амплитуды автоколебаний в системе ………………………10

Заключение …………………………………………………………………………………………  11

         Список используемых источников ………………………………………………………………12

Введение

Особенности поведения нелинейных систем и многообразие процессов в них создают трудности точного их математического описания и теоретического изучения. Во многих случаях возможно и целесообразно заменить реальные нелинейные характеристики некоторыми приближёнными линейными зависимостями.

Одним из методов линеаризации, применим для существенно нелинейных зависимостей, является метод гармонической линеаризации.

 1 Амплитудно – фазовая частотная характеристика линейной части системы

Строим амплитудно – фазовую частотную характеристику линейной части системы Wл(jw), так как . Частотная функция линейной части системы определяется:

;

;

;

.

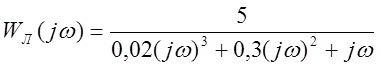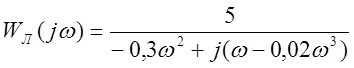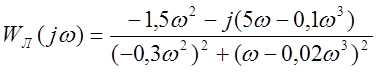Выделяем реальную и мнимую часть:

;              .

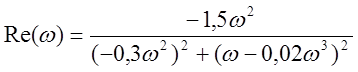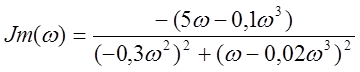Задаёмся значениями w от 0 до ¥ (таблица 1) и строим амплитудно – фазовую характеристику линейной части системы (рисунок 3, 4).

Таблица 1 - Значения для построения АФЧХлинейной части системы

w	10-5	0,2	0,6	0,8	1,4	2,0	2,6	3
Re(w)	-1,5	-1,497	-1,4734	-1,45326	-1,36421	-1,24337	-1,10597	-1,01187
Jm(w)	-¥	-24,93	-8,1266	-5,9777	-3,1208	-1,9065	-1,22621	-0,92193
w	4	5	6	8	20	65	100	¥
Re(w)	-0,78848	-0,6	-0,45203	-0,25692	-0,01765	-0,0002	-3,7Е-05	® 0
Jm(w)	-0,4468	-0,2	-0,07032	0,02997	0,02059	0,00087	0,00025	® 0

Рисунок 3 – АФЧХ линейной части системы

Рисунок 4 – АФЧХ линейной части системы

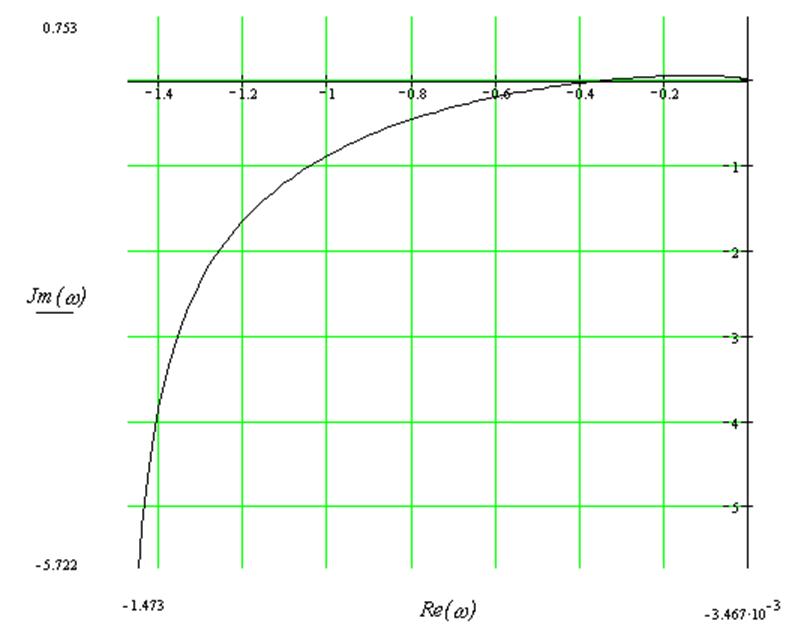(увеличенный участок)

2 Амплитудно – фазовая характеристика нелинейного звена

Гармонически линеаризованная передаточная функция нелинейного звена имеет вид:

.

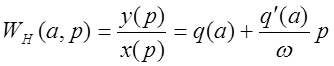Амплитудно – фазовая характеристика нелинейного звена в результате подстановки выражается в форме:

,

где  и  - коэффициенты гармонической линеаризации.

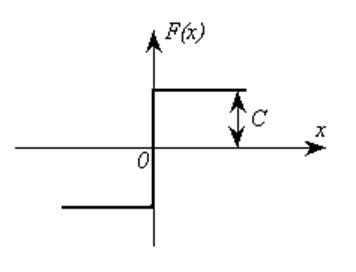
Для заданного нелинейного звена – идеальное реле (рисунок 2) коэффициенты гармонической линеаризации равны:

,                 .

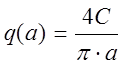Отсюда

.

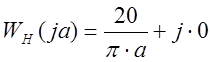Годограф гармонически линеаризованного нелинейного звена определяется следующим образом:

;

;

.

;         .

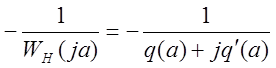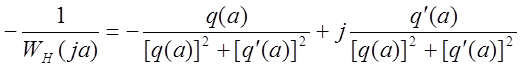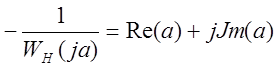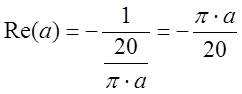Задаёмся значениями а от -¥ до +¥ (таблица 2) и строим АФЧХ линейной части (таблица 1) и годограф гармонически линеаризованного нелинейного звена  (рисунок 5).

Таблица 2 - Значения для годографа гармонически

                                              линеаризованного нелинейного звена

По данным значений таблиц 1 и 2 в одной системе координат строим рассчитанные кривые (рисунок 5).

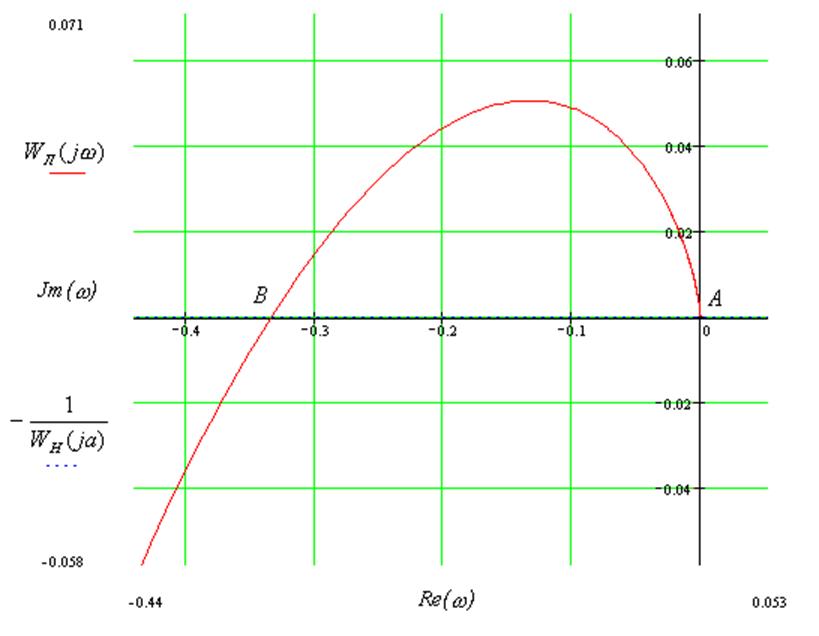Рисунок 5 – АФЧХ линейной части и годограф гармонически линеаризованного нелинейного звена

Годографы  и  пересекаются в двух точках А и В, т.е. означает, что уравнение

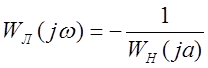
имеет два периодических решения

,         (точка А)

.        (точка В)

            3 Определение частоты и амплитуды автоколебаний в системе

Так как функция 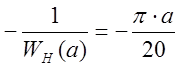 являясь вещественной укладывается на отрицательной вещественной оси, следовательно точка пересечения - А, дает неустойчивое периодическое решение, а вторая точка пересечения - В, имеет устойчивое периодическое решение с амплитудой А₂ » 2,3.

Определяем частоту w₂ автоколебаний в системепо амплитудо–фазовой характеристике линейной части :

, где при .

Тогда при

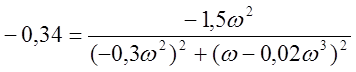  w₂» 7,05 с^-1  (таблица 1).

Следовательно, в  данной системе установятся автоколебания с амплитудой А₂ » 2,3 и частатой w₂» 7,05 с^-1.

Заключение

Произвел исследование устойчивости состояния равновесия или периодических автоколебаний нелинейной системы при помощи метода гармонической линеаризации при заданном типе нелинейности – идеальное реле, а так же расчёт частоты и амплитуды при периодическом колебании системы.

В данной системе системе возможны автоколебания с амплитудой А₂ » 2,3 и частатой w₂» 7,05 с^-1.

Список используемых источников

Дорошенко В.А., Захаров М.И., Зенченко В.М., Шанько А.В. Теория автоматического управления: Методические указания к выполнению лабораторных работ для студентов специальности 21.03 всех форм обучения. – Красноярск: СТИ, 1991. – 24 с.

Зенченко В.М., Шанько А.В. Теория автоматического управления: Методические указания к выполнению контрольных и практических работ для студентов специальности 21.03 всех форм обучения. – Красноярск: СТИ, 1990. – 32 с.