Анализ системы автоматического регулирования на устойчивость по критериям Гурвица, Рауса, Михайлова, Найквиста и по логарифмическим частотным характеристикам, страница 3

w	0	1	4	8	12	16	20	24	28
P(w)	72,864	27,086	-9,827	-4,29783	-1,57067	-0,64621	-0,3024	-0,15734	-0,08903
Q(w)	0	-44,663	-10,439	-0,11511	0,66515	0,49874	0,3274	0,21642	0,14762
w	36	40	45	50	55	60	65	70	75
P(w)	-0,03435	-0,02289	-0,01449	-0,00961	-0,00661	-0,00469	-0,00342	-0,00255	-0,00194
Q(w)	0,0758	0,05668	0,04072	0,03017	0,02295	0,01784	0,01413	0,01138	0,00929

JQ (w)

P (w)

Рисунок 4 - Годограф Найквиста

Лист 10

Рисунок 5 - Увеличенный годограф Найквиста

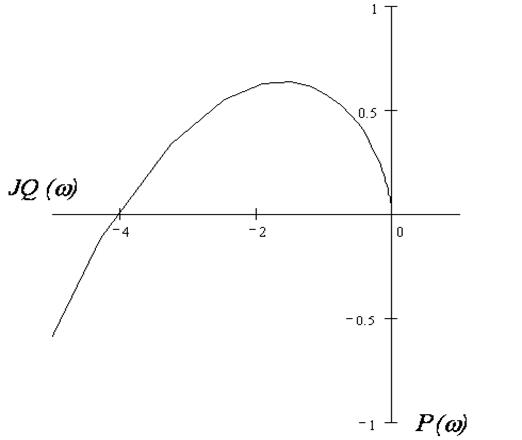
Вывод: система является не устойчивой, так как кривая на рисунках 4 – 5 охватывает точку (-1; j 0) один раз в отрицательном направлении.

2.5 Логарифмический критерий

Записываем передаточную функцию разомкнутой системы:

;

.

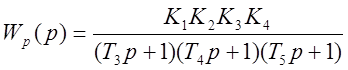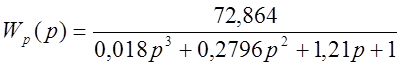Определим значения сопрягающих частот по формулам 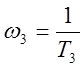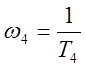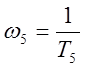(2.2):

;    ;    .         (2.2)

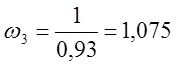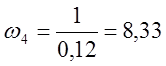c^-1; 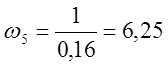  c^-1;   c^-1.

Таблица 2.5 – Данные для построения ЛФЧХ разомкнутой системы

w	j3	j4	j5	j
0	0	0	0	0
1,075	-0,78527	-0,12829	-0,17033	-1,0839
2	-1,0775	-0,23554	-0,3097	-1,62274
3	-1,22664	-0,34556	-0,44752	-2,01971
5	-1,35897	-0,54042	-0,67474	-2,57413
6,25	-1,40042	-0,6435	-0,7854	-2,82932
7	-1,41838	-0,69866	-0,84194	-2,95898
8	-1,43719	-0,76499	-0,90759	-3,10977
8,33	-1,44242	-0,7852	-0,9271	-3,15472
10	-1,46368	-0,87606	-1,0122	-3,35194
25	-1,52781	-1,24905	-1,32582	-4,10268

Фазочастотная  характеристика разомкнутой системы:

суммарная 

.                             (2.3)

   для каждого звена

;

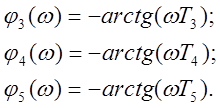                                                        (2.4)

По данным таблицы 2.5 строим ЛФЧХ  разомкнутой  системы (графическая часть).

Вывод:система является статической, т.к.  в передаточной функции разомкнутой системы отсутствует интегрирующее звено. Также система является не устойчивой, т. к. суммарная ЛФЧХ разомкнутой системы пересекает линию  до частоты среза.

	Лист 11

3 Расчет последовательного корректирующего устройства

Основная задача корректирующего устройства – улучшение точности системы и качества переходного процесса и наряду с этим решить и более общую задачу – сделать систему устойчивой, а затем добиться желаемого качества переходного процесса регулирования. Определение корректирующего устройства происходит по частотному методу с помощью логарифмических частотных характеристик.

Строится ЛАЧХ исходной некорректированной системы L_H (графическая часть).

В той   же   системе   строим   желаемую   ЛАЧХ    L_C,   т. е.   характеристику скорректированной системы (графическая часть).

Желаемая ЛАЧХ может быть разбита на три участка: низкочастотный, среднечастотный и высокочастотный.

а – низкочастотный участок  для  статических  систем  представляет  собой горизонтальную прямую, отстоящую от оси частот на величину Дб.

б – среднечастотный участок.

Выбираем значения   по заданным значения t_P и  из таблицы 3.1.

Таблица 3.1

	20%	25%	30%
с –1	7,8 / tP	10 / tP	11,5 / tP
Дб	25	20	16
град	67	57	45
	1,08	1,2	1,28

Через частоту  проводим прямую под наклоном –20 Дб/дек до значения  Дб и Дб. В этих точках прямая меняет свой наклон для положительного Дб () на   -40 Дб/дек, для отрицательного Дб () на –60Дб/дек. Пряма с наклоном –40Дб/дек проводится до пересечения с прямой Дб. Наклон соответствующий –60Дб/дек соответствует в – высокочастотному участку.

Путем вычитания ординат исходной ЛАЧХ L_Hиз ординат желаемой ЛАЧХ L_C получаем ЛАЧХ  корректирующего эвена L_К (графическая часть).

По полученной ЛАЧХ корректирующего звена подбираем наиболее простое по техническому исполнению корректирующее устройство соответствующей формы и вносим эти данные в таблице 3.2.

	Лист 13

Таблица 3.2- Элементы корректирующего устройства

Схема	Передаточная функция	Параметры схемы
		;; ; ;; R1=18,1 Ом; R2=1 Ом; R3=3,2 Ом;   C1=0,93 Ф; k1=k4=0,15.
		;; ;;;    R4=1 Ом; R5=0,16 Ом;C2=0,16 Ф; k2=0,1375.
		;; ;;;    R6=1 Ом; R7=0,22 Ом; C3=0,12 Ф; k3=0,18.