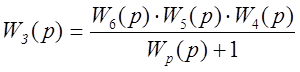Анализ системы автоматического регулирования на устойчивость по критериям Гурвица, Рауса, Михайлова, Найквиста и по логарифмическим частотным характеристикам, страница 2

.                            (1.2)

.

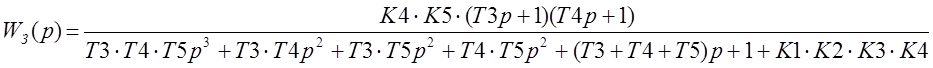
Подставим числовые значения в выражение (1.2):

.

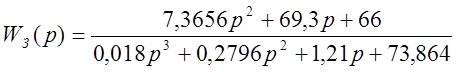Коэффициенты характеристического уравнения для замкнутой системы:

АПП.000000.027. ПЗ Лист 6 Изм Лист № докум. Подп. Дата

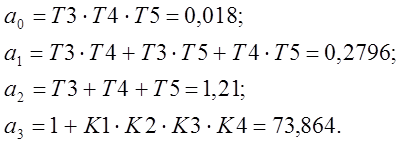
2 Исследование на устойчивость

2.1 Критерий Гурвица

Чтобы система была устойчивой необходимо и достаточно, чтоб главный определитель матрицы Гурвица и все его диагональные миноры были не отрицательны.

   Критерий Гурвица предполагает исследование замкнутой системы по ее характеристическому многочлену:

.

По коэффициентам этого многочлена составляем квадратную матрицу следующего вида: 

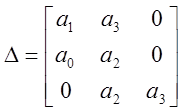.                                                                   (2.1)

Найдем главный и диагональные миноры матрицы (2.1):

;

;

.

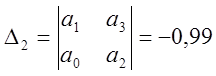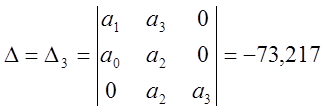Вывод:Данная система в замкнутом состоянии неустойчива, т.к.  главный и один из диагональных миноров отрицательны.

2.2 Критерий Рауса

 Для определения устойчивости системы по коэффициентам характеристического уравнения замкнутой системы, Раус предложил правило оформленное в виде таблицы:  

    Таблица 2.1 – Таблица Рауса

а0	а2	а4	а6
а1	а3	а5	а7
a1a2-a0a3  b1=        a1	а1a4-a0a5 b2=      a1	a1a6-a0a7 b3=       a1	а1a8-a0a9   b4=       a1	×××
b1a3-a1b2 c1=        b1	b1a5-a1b3 c2=       b1	b1a7-a1b4 c3=      b1	B1a9-a1b5 c4=       b1	×××
c1b2-b1c2 d1=  c1	с1b3-b1c3 d2=   c1	c1b4-b1c4 d3=   c1	C1b5-b1c5 d4=   c1	×××
×××	×××	×××	×××	×××

Выписываем характеристический многочлен и вычисляем коэффициенты таблицы Рауса:

.

	Лист 7

Таблица 2.2 – Коэффициенты таблицы Рауса

Вывод: Данная система в замкнутом состоянии неустойчива, т.к. не все коэффициенты первого столбца таблицы Рауса положительны.

3  Критерий Михайлова

Для устойчивости АСР n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости, обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль.

Выписываем характеристическое уравнение замкнутой АСР:

.

Производим подстановку P = (jw):

;

.

Выделяем вещественную и мнимую часть многочлена:

.

Задаём значения  0 £w<¥  и считаем U(w), V(w):

Таблица 2.3 – Данные для построения годографа Михайлова

w	0	1	4	8	12	16	20	24	28	32
U(w)	73,864	73,584	72,745	71,627	70,509	69,390	68,272	67,1536	66,0352	64,9168
V(w)	0	1,192	3,688	0,464	-16,584	-54,368	-119,8	-219,792	-361,256	-551,104
w	36	40	45	50	55	60	65	70	75	80
U(w)	63,7984	62,68	61,282	59,884	58,486	57,088	55,69	54,292	52,894	51,496
V(w)	-796,24	-1103,6	-1585,8	-2189,5	-2928,2	-3815,4	-4864,6	-6089,3	-7503	-9119,2

	Лист 8

По данным (таблицы 2.3) строим годограф Михайлова (рисунок 3).

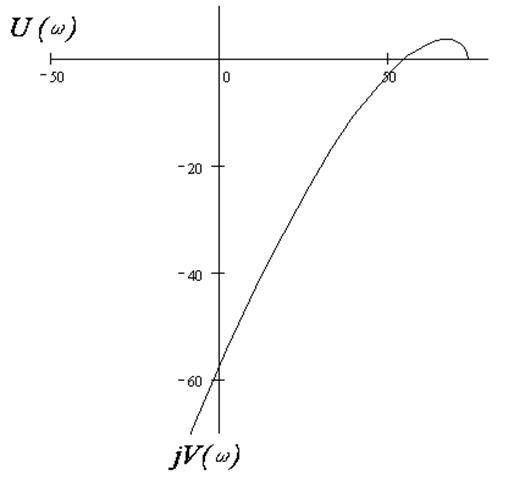Рисунок 3 - Годограф Михайлова

Вывод: система не устойчива, так как годограф Михайлова, начав движение от вещественной положительной оси комплексной плоскости в положительном направлении (против часовой стрелки) последовательно не пересек n – квадрантов и обратился в ноль.

4  Критерий Найквиста.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по АФЧХ разомкнутого контура АСР.

Записываем передаточную функцию  разомкнутой АСР (рисунок 2):

.

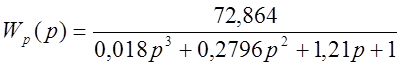Делаем замену P = (jw) и подставляем в данное уравнение:

.

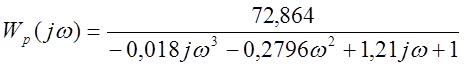Выделяем в знаменателе действительную и мнимую частьи помножаем на сопряженное:

.

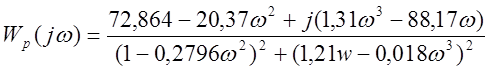Выписываем вещественную и мнимую части:

Лист 9

;

;

.

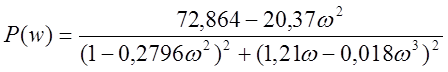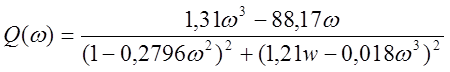По данным (таблицы 2.4) строим годограф Найквиста (рисунок 4).

Таблица 2.4 – Данные для построения годографа Найквиста