Тема: « Определение динамических характеристик объектов управления по кривым разгона »
Выполнил: ст-т гр. 24-2
Данилов Д.В.
Проверили:
Титович Л.В.
Тяпкин В.Н.
В данной лабораторной работе проводится исследование объекта первого порядка при наличии асимптоты у кривой разгона.
Одноемкостный объект описывается линейным дифференциальным уравнением первого порядка
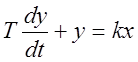
где Т—постоянная времени объекта;
k — коэффициент усиления объекта.
Решением такого дифференциального уравнения при![]() , т.е. при скачкообразном входном
возмущении, величиной
, т.е. при скачкообразном входном
возмущении, величиной ![]() является
переходная функция
является
переходная функция
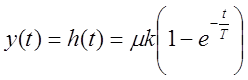 (1)
(1)
Параметры одноемкостного объекта определяются из кривой разгона известными методами. Коэффициент усиления находится из формулы
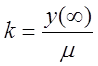 (2)
(2)
где ![]() - численное значение (в
данном масштабе) отрезка, отсекаемого на оси ординат асимптотой к кривой
разгона;
- численное значение (в
данном масштабе) отрезка, отсекаемого на оси ординат асимптотой к кривой
разгона;
![]() — величина скачка входного
параметра.
— величина скачка входного
параметра.
Постоянную времени Т можно определить несколькими способами. При графическом способе обработки Т определяют как отрезок, отсекаемый касательной к кривой разгона на асимптоте, или время, в течение которого кривая разгона достигает значения 0,63 у(¥). Эти способы, однако, не дают большой точности и ведут к появлению субъективных ошибок.
При машинной обработке кривой разгона удобнее применить другой способ. Экспонента обладает тем свойством, что длина подкасательной в любой точке равна постоянной времени (рисунок 1).
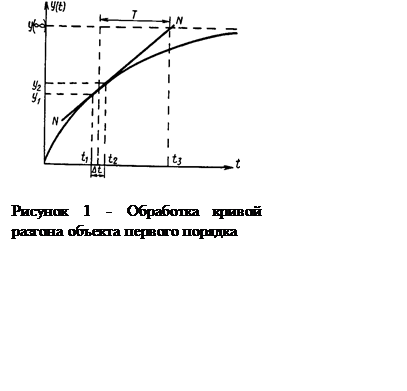 Найдем уравнение линии NN и найдем из
него время
Найдем уравнение линии NN и найдем из
него время ![]()
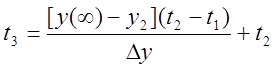 ,
,
отсюда
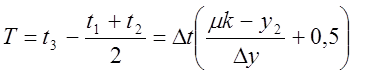 (3)
(3)
где ![]() ,
, ![]() .
.![]()
Очевидно, что прямая, проведенная через две точки кривой
разгона, тем ближе к касательной, чем ближе расположены эти точки друг к другу.
Следовательно, для повышения точности следует брать соседние точки. Имея в
виду, что замеры на реальной кривой произведены через равные промежутки времени
![]() и вычисляя Т по соседним
точкам
и вычисляя Т по соседним
точкам ![]() и
и ![]() преобразуем формулу (3):
преобразуем формулу (3):
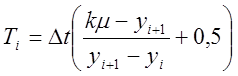 (4)
(4)
В результате такого расчета для n
пар соседних точек получим п значений Т, по которым вычислим ![]()
![]() :
:
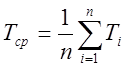 (5)
(5)
При таком определении существенно повышается точность, так как определение производится многократно, что исключает случайные ошибки, и в определении участвуют все точки кривой.
В соответствии с выданным преподавателем вариантом получаем следующий график кривой разгона объекта первого порядка (рисунок 2):
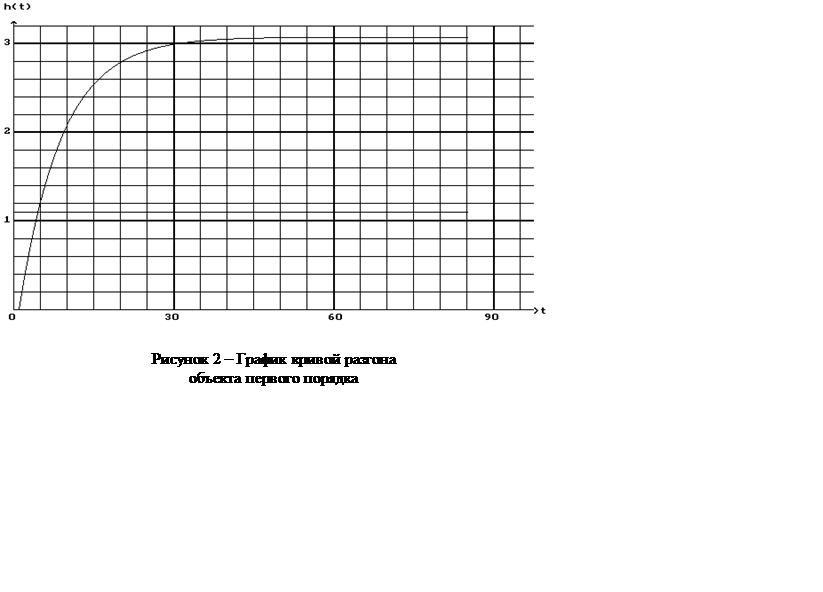 |
m
= 1,1;
y(¥) = 3,09.
Найдем коэффициент усиления k:
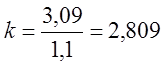 .
.
С помощью ЭВМ вычисляем ординаты точек на кривой разгона. Для повышения точности расчетов берем соседние точки. Принимаем Dt = 10c = 1/6 мин.
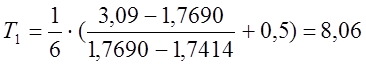 ;
;
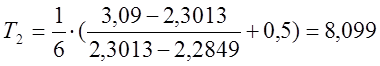 ;
;
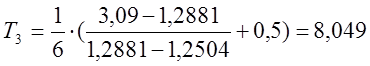 ;
;
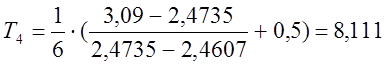 ;
;
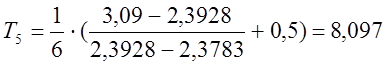 .
.
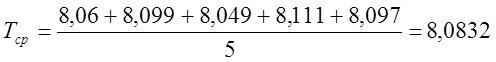 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.