Пример построения модели технологического процесса

Лекционные материалы (Пример) .

ОГЛАВЛЕНИЕ.

1. Пример построения модели технологического процесса.

1.1. Содержательное описание процесса.

1.2. Формализованная схема

1.3. Математическая модель.

1.4. Модель математическая логическая имитационная.

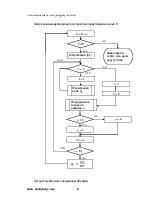
1.4.1. Структура моделирующего алгоритма.

1.5. Модель математическая логическая аналитическая (численный метод решения задачи).

Пример.

МАТЕРИАЛЫ

Данный пример имеет целью проиллюстрировать процесс создания математической модели.

1.1.  Содержательное описание процесса.

Исследуется процесс изготовления и сборки роликовых подшипников. Исследование посвящено определению оптимальных интервалов между последовательными подналадками оборудования, изготавливающего ролики для подшипников.

Известно, что уменьшение интервалов времени между подналадками оборудования ведет к увеличению числа сотрудников и, как следствие, расходов на их содержание. Увеличение интервалов – к увеличению брака.

Производственный эксперимент невозможен ввиду его дороговизны и значительного риска.

Определим круг сведений, необходимых для решения задачи, в виде описания существа вопроса и соответствующих числовых данных.

Подшипник содержит в своем составе два кольца, сепаратор и ролики.

●  Различные типы подшипников могут содержать различное число роликов от n₁ до n₂.

●  Основным фактором, определяющим качество подшипника, является однородность диаметров роликов.

●  Подшипник считается годным, если разброс диаметров роликов не превышает заданной величины δ (дельта).

В результате наблюдения за работой оборудования установлено, что по мере увеличения продолжительности работы оборудования между подналадками разброс диаметров роликов растет.

 Данные о разбросе диаметров роликов были обработаны следующим образом.

●  Весь интервал времени между подналадками (0,Т) был разбит на под интервалы (0,t₁), (t₁,t₂),…, (t_r-1,t_r).

●  Ролики, изготовленные в течение каждого из интервалов времени, разбивались на группы в соответствии с их диаметром (z₁, z₂), (z₂, z₃), …, (z_p-1, z_p).

В результате длительного наблюдения за производственным процессом удалось определить частоты h_i,j попадания роликов в определенные группы по диаметру для различных интервалов времени.

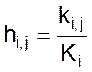                           (частота как функция времени)                               (01)

где     K_i – количество всех роликов, изготовленных в течение интервала времени(t_i-1, t_i);

          k_i,j – количество той части из них, которая имеет диаметры в пределах (z_j, z_j+1).

Полученные результаты были представлены в виде таблицы 1.

Таблица 1.

Учитывая изложенное, требуется:

■  дать математическую формулировку задачи об определении зависимости доли бракованных подшипников от длительности интервалов между подналадками оборудования;

■  подготовить задачу для решения на ЦВМ;

■  выполнить решение и дать интерпретацию полученных результатов.

1.2.  Формализованная схема.

Основой формализованной схемы процесса является точная формулировка задачи. Для того чтобы ее получить необходимо начать с представления в формальном виде сведений, имеющихся в содержательном описании процесса.

Обозначив диаметры роликов через z_i, мы можем представить их как совокупность чисел {z_i}. Таким образом, в дальнейшем вместо роликов мы будем рассматривать числа, и оперировать с этими числами.  Так как погрешность изготовления роликов имеет случайный характер, совокупность чисел  {z_i} можно рассматривать как возможные значения случайной величины ξ (кси), образующей генеральную совокупность.

Для комплектации очередного i-го подшипника из генеральной совокупности извлекается случайная выборка, содержащая n роликов (чисел в нашем случае z_i1, z_i2…z_in). В выборке всегда будет содержаться два числа, z_imax и z_imin разность между которыми, называется размахом выборки  (z_max – z_min)  < δ .

Подшипник будем считать годным, если размах выборки не превышает заданной величины δ (дельта).

Пусть за некоторый интервал времени изготовлено M подшипников, каждый из которых представляет собой выборку из генеральной совокупности, при этом m из них оказались годными, а (M – m) бракованными. Тогда величина «р»

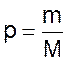                                                                                                                (02)

будет представлять долю годных изделий, а «q»

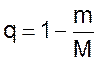                                                                                                            (03)

долю бракованных изделий.

Отметить!!!   Для того чтобы использовать показатель «доля бракованных изделий» q в качестве объективной характеристики процесса, необходимо принять меры для обеспечения его статистической устойчивости.

Продолжая формализацию процесса, распишем несколько вариантов математических схем и предложим их для рассмотрения авторам содержательного описания, чтобы они могли выбрать схему достаточно близкую к реальной картине явлений. После чего сформулируем конкретный перечень недостающих требований.

Схема I.

●  Начало отсчета времени t = 0 совпадает с моментом начала работы линии после подналадки.

●  Изготовленные ролики поступают непосредственно на сборку.

●  По мере удаления от начала отсчета времени разброс диаметров роликов увеличивается.

●  По мере удаления от начала отсчета времени доля бракованных подшипников увеличивается.

При указанных предпосылках можно вариант формализации представить следующим образом:

●  рассматривается случайная функция ξ(t) (кси от t), вероятностные характеристики которой: математическое ожидание , корреляционная функция  или соответствующие многомерные распределения являются функциями времени t;

●  показатели: вероятность значения размаха выборки и доля бракованных подшипников так же являются функциями времени t.

Относительно схемы I можно сделать два заключения:

●  Имеющиеся статистические данные (таблица 1) характеризуют одномерный закон распределения случайной функции ξ(t), что недостаточно для решения задачи (необходимы многомерные законы распределения).

●  При моделировании необходимо сформировать большое количество реализаций (N) рассматриваемого процесса, чтобы определить статистически устойчивое значение средней доли брака

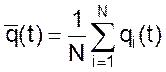                                                                                                  (04)

как функцию времени по результатам N реализаций.

Схема II.

●  Изготовление роликов и сборка подшипников не связаны между собой хронологически. После изготовления ролики поступают на склад, поэтому для данного экземпляра подшипника могут быть использованы ролики, изготовленные в любое время.

●  Разброс диаметров роликов в партии, хранящейся на складе, а также в совокупности, доставляемой на сборку, зависит от интервалов времени подналадки оборудования T.

●  Если T увеличивается, то и разброс диаметров роликов в выборках увеличивается и, как следствие, увеличивается доля бракованных подшипников.

Для данной процедуры формирования совокупности {z_i} формализация будет отличной от предыдущей.

В этом случае рассматривается случайная величина ξ (кси), вероятностные характеристики которой (математическое ожидание , дисперсия , функция распределения ) зависят от параметра T (времени между подналадками). Естественно, что показатели: вероятность размаха выборки и доля бракованных подшипников являются функциями T.

 Изложенное для схемы, II позволяет сделать два вывода.