Пример построения модели технологического процесса, страница 2

●  Первый вывод связан с порядком определения доли брака по результатам моделирования. Поскольку процесс изготовления роликов не связан синхронно со сборкой подшипников, нет необходимости моделировать все N реализаций процесса. Допустимо иметь единственную реализацию, если число выборок из генеральной совокупности достаточно велико. 

●  Второй вывод заключается в том, что схема II позволяет использовать статистические данные, характеризующие разброс диаметров в выборках (таблица 1). Однако форма записи, принятая в табл.1, не совсем приемлема. Она соответствует оценке одномерного закона распределения случайной функции времени ξ(t). Нас же интересует оценка закона распределения случайной величины ξ(T) (кси от T): разброса диаметров роликов в зависимости от величины интервала времени между подналадками оборудования. Чтобы представить в таблице требуемый закон распределения, сформируем ее заново таким образом, чтобы в ней содержались частоты  попадания z_i в соответствующие интервалы z₁…z₂; z₂…z₃; . . . z_p-1…z_p как функции параметра T.

Рассмотрим подробнее различия в способах определения частот  и . Напомним, что первая определялась как 

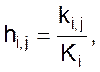                                                                                                           (05)

где     Ki – количество всех роликов, изготовленных в течение интервала времени (t_i-1, t_i);

          k_i,j – количество той части из них, которая имеет диаметры в пределах (z_j, z_j+1).

Таким образом,  являются частотами, полученными по результатам измерения диаметров роликов, изготовленных только в течение интервала времени (t_i-1, t_i).

Вторая же,  вычисляется в соответствии с выражением

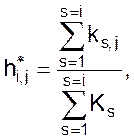                                                                                                      (06)

где суммирование распространяется на все индексы s соответствующие  накопленным интервалом времени (0, T_i).

В этом случае  являются накопленными частотами, полученными по результатам измерения диаметров роликов, изготовленных в течение интервалов времени (0, T_i), то есть в интервалах (0, t₁) + (0, t₂) + (0, t₃)+ … +(0, t_r).

На базе таблицы 1 сформируем таблицу 2 в виде

Таблица 2.

Время.		Диаметры роликов
		1 (Z1 − Z2)	2 (Z2 − Z3)	…	P– 1 (Zp-1 − Zp)
1	0 …T1			…
2	0 …T2			…
3	0 …T3			…
…	…	…	…	…	…
r	0 …Tr			…

Будем предполагать, что авторы содержательного описания одобрили вторую схему.

1.3.  Математическая модель.

Для того чтобы превратить формализованную схему в математическую модель необходимо установить соотношения, связывающие фигурирующие в формализованной схеме величины.

Рассматривается случайная величина ξ (кси), имеющая функцию распределения F_ξ(z) или плотность вероятностей f_ξ(z). Обе функции зависят от параметра T. Совокупность {z_i}_T представляет собой множество возможных значений случайной величины ξ при фиксированном значении параметра T – генеральную совокупность.

Из генеральной совокупности извлекаются случайные выборки z₁, z₂, …z_n объема n. Для каждой выборки определяется размах

                                                                                                    (07)

Пусть μ – величина, равная 1, если    (подшипник годен) и равная 0 в противоположном случае.

Тогда количество годных подшипников из M рассмотренных равно

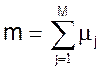,                                                                                                          (08)

а количество бракованных

                                                                                                       (09)

Отсюда доля годных подшипников равна

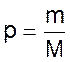                                                                                                               (10)

и доля бракованных

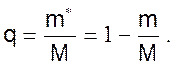                                                                                                 (11)

Количество выборок M назначается из соображений статистической устойчивости величины q.

В результате исследования необходимо установить зависимость величины q от параметра T:

                                                                                                           (12)

Будем проводить аналогичные вычисления при нескольких значениях T с шагом t:

                                                                                                     (13)

Рассмотрим получение закона распределения случайной величины ξ (кси).

При моделировании удобно пользоваться функцией плотности вероятностей f_ξ(z). В качестве приближения для функции плотности f_ξ(z) будем пользоваться ступенчатой функцией с ординатами f_i,j, вычисляемыми по формуле

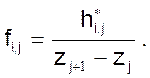                                                                                                    (14)

Для удобства последующей машинной реализации полученные значения ординат можно аппроксимировать подходящими аналитическими выражениями (нормального, показательного или других законов распределения).

Теперь, разрешив все вопросы, можно выписать соотношения математической модели:

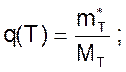                                                                                                       (15)