Пример построения модели технологического процесса, страница 4

Оператор 3. Подготавливает сведения о законе распределения случайной величины x (интерполирование, нормировка и т.д.). Управление передает оператору 4.

Оператор 4. Проверяет условие  k < n (k – количество роликов, отобранных для комплектации очередного подшипника,  n – заданное количество роликов в очередном подшипнике.).

ЕСЛИ (k < n)

     ТО - управление передает оператору 5.

     ИНАЧЕ – управление передает оператору 7.

Оператор 5. Увеличивает значение k (количество роликов в данном подшипнике) на 1. Управление передает оператору 8.

Оператор 6. Формирует очередное случайное значение диаметра ролика z_k. Управление передает оператору 4.

Оператор 7. Увеличивает значение n (количество готовых подшипников) на 1. Управление передает оператору 8.

Оператор 8.  Обнуляет значение k. Управление передает оператору 9.

Оператор 9. Определяет значение z_max в собранном подшипнике. Управление передает оператору 10.

Оператор 10. Определяет значение z_min в собранном подшипнике. Управление передает оператору 11.

Оператор 11. Вычисляет значение размаха для данного подшипника. Управление передает оператору 12.

Оператор 12. Сравнивает полученное значение размаха с предельно допустимым заданным значением.

ЕСЛИ (u £ d)

     ТО - управление передает оператору 13.

     ИНАЧЕ - управление передает оператору 14.

Оператор 13. m присваивает значение 1. Управление передает оператору 15.

Оператор 14. m присваивает значение 0. Управление передает оператору 15.

Оператор 15. Формирует значение показателя «Количество годных подшипников» m_t. Управление передает оператору 16.

Оператор 16.  Проверяет, не достигло ли количество собранных подшипников заданной величины.

Если (n < M_T)

     ТО - управление передает оператору 4.

     ИНАЧЕ - управление передает оператору 17.

Оператор 17. Определяет долю бракованных подшипников в данном очередном интервале времени между подналадками T_s. Управление передает оператору 1.

Оператор 18. Формирует результаты моделирования для выдачи на регистрацию. Управляет процессом регистрации. Заканчивает процесс моделирования.

Перейдем к рассмотрению еще двух методов исследования процесса: численного и аналитического. Необходимо отметить, что оба этих метода исследования применимы только тогда, когда модель представлена в виде комбинации знаковых логических выражений и уравнений искомых величин.

1.5.  Модель математическая логическая аналитическая (численный метод решения задачи).

Предположим, что параметры закона распределения случайной величины могут изменяться для различных интервалов T, но сам закон слабо зависит от параметра T. Отметим, что в данном случае это предположение обязательно.

Пусть f_x(z) – плотность распределения величины x при некотором фиксированном значении параметра T. Доля  брака при изготовлении подшипников  равна  вероятности  того, что u ³ d.

Рассмотрим  вероятность  противоположного события  A, состоящего в том, что u < d.

Событие А может осуществиться в одном из вариантов A_i, когда некоторая величина z_i из выборки объема n попадет в интервал (z, z + dz), а остальные n – 1 величин этой выборки расположатся внутри интервала (z, z + d). Легко видеть, что таких вариантов будет n, в зависимости от того, какая из величин выборки попадет в интервал (z, z + dz).

Вероятность любого события A_i при фиксированном значении z равна

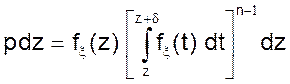                                                             (21)

По формуле полной вероятности перейдем к вероятности события A (хотя бы одного из событий A_i) при произвольном значении z:

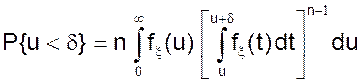                                                   (22)

Тогда долю бракованных подшипников как вероятность противоположного события можно записать (при фиксированном значении T) в виде

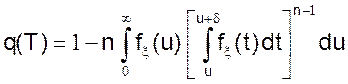                                                     (23)

Последнее соотношение, выражающее долю брака q как функцию T и n, и является численным решением задачи.

Для определения значений q(T) можно использовать любой типовой численный метод нахождения квадратур.

Необходимо отметить, что изменение искомых величин влечет за собой коренное изменение системы уравнений, а поэтому и метода численного решения задачи.

1.6.  Модель математическая логическая аналитическая (аналитический метод решения задачи).

Для аналитического решения задачи,  сделаем предположение о типе распределения f_x(z).

Наиболее близким к реальности, на взгляд разработчиков содержательного описания процесса, является показательный закон, плотность распределения которого имеет вид.

                                                                                    (24)

При сделанных предположениях для определения доли брака можно воспользоваться соотношением (23):

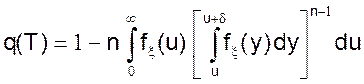                                                   (25)

Вычислим внутренний интеграл, при этом воспользуемся вместо f(y) выражением (24)

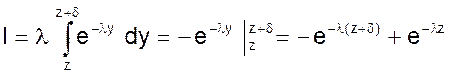                                      (26)

или

                                                                             (27)

Тогда

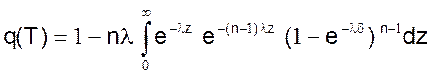                                         (28)

Вынося за знак интеграла величины, не зависящие от z, получим

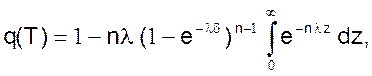                                                  (29)

учитывая, что

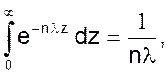                                                                               (30)

в окончательном виде можно записать

                                                                    (31)

В данном выражении функцией T является параметр l.

Рассмотренный  пример показывает различие между имитационным, численным и аналитическим методами решения задачи.