Оптимальная производственная программа

Задача 12. Оптимальная производственная программа

12.1. Постановка задачи

Фирма выпускает два вида изделий А и В, которые обрабатываются на станках двух типов. Известны нормативы a_ij времени, требуемого для обработки одного изделия j-го вида на станке i-го типа (ст./час.), общие фонды рабочего времени каждого типа станков b_i (ст./час.). Фирма имеет контракт, согласно которому должна ежедневно поставлять заказчику d₁ изделий А и d₂ изделий В.

Удельная прибыль р_j = c_j – l·х_j, где х_j — количество проданных изделий j-го вида, а c_j, l — фиксированные величины.

Требуется определить: сколько изделий каждого вида нужно изготовить фирме, чтобы прибыль от их реализации была максимальной.

→ Задание 1: Составить математическую модель нахождения оптимального плана выпуска продукции.

→ Задание 2: Определить оптимальный план выпуска обобщенным методом множителей Лагранжа.

→ Задание 3: Дать геометрическую интерпретацию хода решения задачи.

→ Задание 4: Дать экономическую интерпретацию полученных результатов

12.2. Исходные данные

а11	a12	a21	a22	b1	b2	d1	d2	c1	c2	l
2	2	6	2	160	220	10	20	320	280	2

12.3. Построение математической модели (выполнение задания 1)

Z = (320 – 2х₁) х₁  + (280 – 2х₂) х₂ = 320 х₁ – 2 + 280 х₂ – 2.

где х₁ — план выпуска изделий А; х₂ — план выпуска изделий В.

Исходная задача:

Z = 320х₁ – 2 + 280 х₂ – 2 → max,                                                                       (1)

                                                            2х₁ + 2х₂ ≤ 160,                 (2)

                                                            6х₁ + 2х₂ ≤ 220,                 (3)

                                                            х₁ ≥ 10,  х₂ ≥ 20.                (4)

12.4. Нахождение оптимального плана обобщенным методом множителей Лагранжа (выполнение задания 2)

·  Проверка условий выпуклого программирования

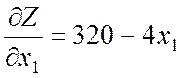 и  ,

; 

;

.

.

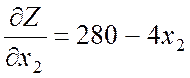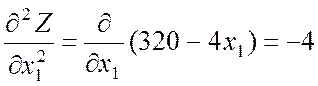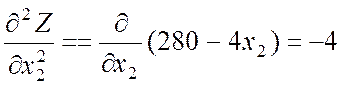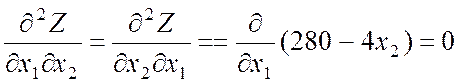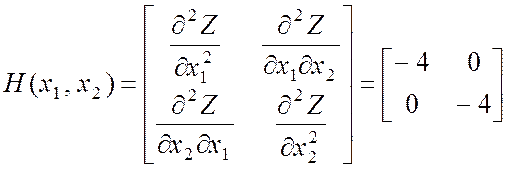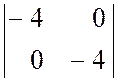 = (-4)·(-4) – 0·0 = 16.

→ Значения обоих миноров не зависят от точки х = (x₁, x₂),

→ Минор первого (нечетного) порядка отрицателен,

→ Минор второго (четного) порядка положителен.

→ЦФ — строго вогнутая функция (теорема 1)

→ задача (1) – (3) - задача выпуклого программирования

→  имеется единственное оптимальное решение.

·  Многошаговая процедура поиска оптимального решения обобщенным методом множителей Лагранжа

Шаг 1.  → Задача 1: Z = 320х₁ – 2 + 280 х₂ – 2 → max.      

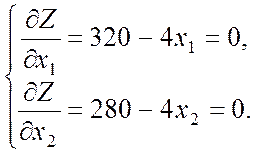→  →   = (80, 70)   → точка  глобального максимума ЦФ.  

2×80 + 2×70 = 160 + 140 = 300 > 160

 → = (80, 70)  не  является оптимальным решением исходной задачи (1) – (4).

Шаг 2.  → Задача 2:  Z = 320х₁ – 2 + 280х₂ – 2 → max,                            (5)

                                                           2х₁ + 2х₂  = 160.                (6)

→ L(x₁, x₂, λ) = 320х₁ – 2 + 280х₂ – 2 + λ (160 – 2х₁ – 2х₂)

         ,  .

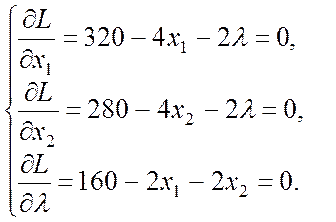
 160 – 2×(80 – 0.5λ) – 2×(70 – 0.5λ) = 0    2λ – 140 = 0     λ = 70.

→ = (45, 35) , =70.

         6×45 + 2×35 = 270 + 70 = 340 > 220 

→ = (45, 35) не  является оптимальным решением исходной задачи (1) – (4).

Шаг 3.  → Задача 3:  Z = 320х₁ – 2 + 280 х₂ – 2 → max,                      (7)

                                                            6х₁ + 2х₂ = 220.                (8)

L(x₁, x₂, λ) = 320х₁ – 2 + 280 х₂ – 2 + λ (220 – 6х₁ – 2х₂)

,  .

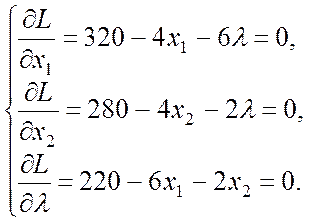
 220 – 6 (80 – 1.5λ) – 2×(70 – 0.5λ) = 10λ – 400 = 0     λ = 40.

→ = (20, 50) , =40.

2×20 + 2×50 = 40 + 100 = 140 < 160,

→ = = (20, 50)   → Z^* = 320×20 – 2×20² + 280×50 – 2×50² = 14 600.

12.5. Геометрическая интерпретация хода решения задачи (выполнение  Задания 3)

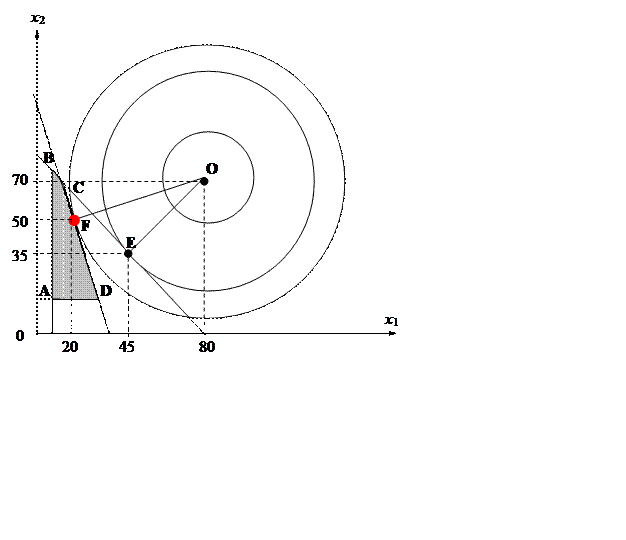Область допустимых решений задачи фирмы - выпуклый четырехугольник АВCD. Линии уровня ЦФ - концентрические окружности, имеющие общий центр в точке О (80, 70).  

Оптимальное решение задачи  1 — точка О (= (80, 70)) , задачи 2  — точка Е (= (45, 35)) , задачи 3 и исходной задачи - точка F (= = (20, 50)).

12.6. Экономическая интерпретация полученных результатов (выполнение задания 4)

Z^* =  14 600 при = (20, 50), ,  , = 40.