«Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они составлены из идей... Узоры математика так же, как узоры художника или поэта, должны быть прекрасны; идеи так же, как цвета или слова, должны соответствовать друг другу. Красота есть первое требование: в мире нет места для некрасивой математики».
Г.Х.Харди
В первой главе отмечалось, что существуют первообразные довольно простых функций, которые уже нельзя выразить через элементарные функции. В связи с этим, огромное практическое значение приобретают те классы функций, о которых можно точно сказать, что их первообразные – элементарные функции. К такому классу функций относятся рациональные функции, представляющие собой отношение двух алгебраических многочленов. К интегрированию рациональных дробей приводят многие задачи. Поэтому очень важно уметь интегрировать такие функции.
Рациональной дробью (или дробно-рациональной функцией)называется отношение двух алгебраических многочленов:
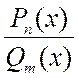 ,
(2.1.1)
,
(2.1.1)
где
![]() и
и ![]() –
многочлены.
–
многочлены.
Напомним, что многочленом (полиномом, целой рациональной функцией) n-й степени называется функция вида
![]() , (2.1.2)
, (2.1.2)
где
![]() – действительные числа. Например,
– действительные числа. Например,
![]()
– многочлен первой степени;
![]()
– многочлен четвертой степени и т.д.
Рациональная дробь (2.1.1) называется правильной, если степень ![]() ниже
степени
ниже
степени ![]() , т.е. n<m,
в противном случае дробь называется неправильной.
, т.е. n<m,
в противном случае дробь называется неправильной.
Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби (дробной части). Выделение целой и дробной частей неправильной дроби можно производить по правилу деления многочленов «уголком».
Пример 2.1.1. Выделить целую и дробную части следующих неправильных рациональных дробей:
а) 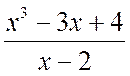 , б)
, б) 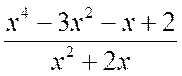 .
.
Решение. а) Используя алгоритм деления «уголком», получаем
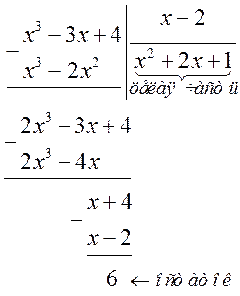
Таким образом, получаем
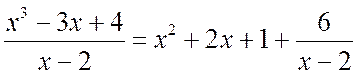 .
.
б) Здесь также используем алгоритм деления «уголком»:
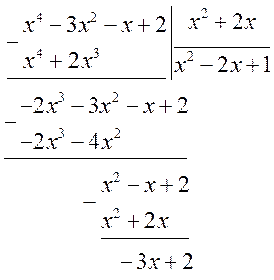
В результате, получаем
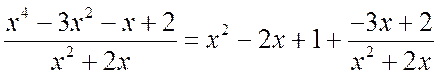 .
.
Подведём итоги. Неопределённый интеграл от рациональной дроби в общем случае можно представить суммой интегралов от многочлена и от правильной рациональной дроби. Нахождение первообразных от многочленов не представляет трудностей. Поэтому в дальнейшем будем рассматривать в основном правильные рациональные дроби.
Среди правильных рациональных дробей выделяют четыре типа, которые относят кпростейшим (элементарным) рациональным дробям:
|
1) |
2) |
3) |
4) |
где ![]() – целое число,
– целое число, ![]() , т.е. квадратный трёхчлен
, т.е. квадратный трёхчлен ![]() не
имеет действительных корней.
не
имеет действительных корней.
Интегрирование простейших дробей 1-го и 2-го типа не представляет больших трудностей:
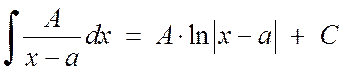 , (2.1.3)
, (2.1.3)
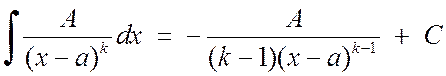 . (2.1.4)
. (2.1.4)
Рассмотрим теперь интегрирование простейших дробей 3-го типа, а дроби 4-го типа рассматривать не будем.
Начнём с интегралов вида
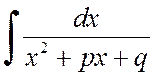 .
.
Данный интеграл обычно вычисляют путем выделения полного квадрата в знаменателе. В результате получается табличный интеграл следующего вида
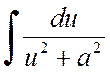 или
или 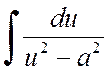 .
.
Пример 2.1.2. Найти интегралы:
а) 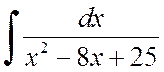 , б)
, б) 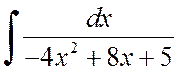 .
.
Решение. а) Выделим из квадратного трёхчлена полный квадрат:
![]() .
.
Отсюда находим
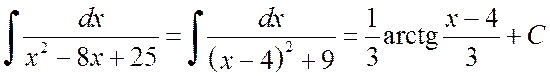 .
.
б) Выделив из квадратного трёхчлена полный квадрат, получаем:
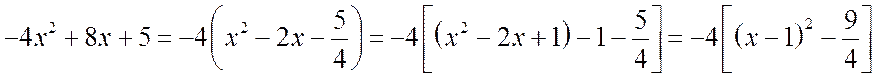 .
.
Таким образом,
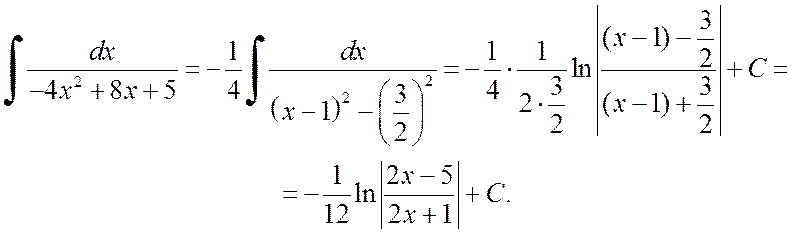 .
.
Для нахождения интеграла
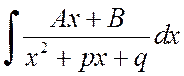
можно
выделить в числителе производную знаменателя и разложить интеграл на сумму двух
интегралов: первый из них подстановкой ![]() сводится
к виду
сводится
к виду
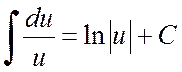 ,
,
а второй – к рассмотренному выше.
Пример 2.1.3. Найти интегралы:
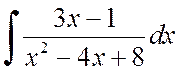 .
.
Решение. Заметим,
что 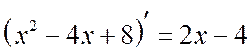 . Выделим в числителе производную
знаменателя:
. Выделим в числителе производную
знаменателя:
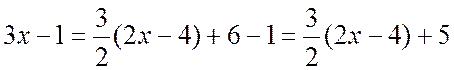 .
.
Тогда
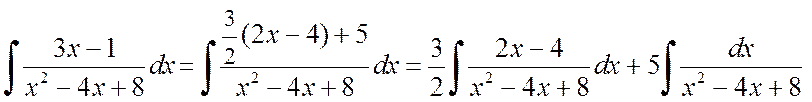 .
.
Первый
интеграл вычисляется при помощи подстановки ![]() :
:
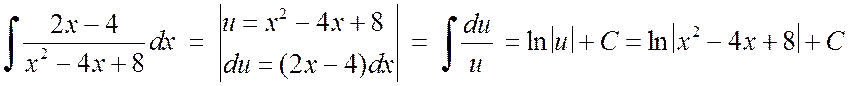 .
.
Во втором интеграле выделим полный квадрат в знаменателе
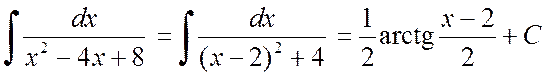 .
.
Окончательно, получаем
Любую правильную рациональную дробь ![]() можно представить единственным
образом в виде суммы простейших дробей. Для этого знаменатель
можно представить единственным
образом в виде суммы простейших дробей. Для этого знаменатель ![]() нужно разложить на множители. Из высшей алгебры известно, что каждый многочлен с
действительными коэффициентами
нужно разложить на множители. Из высшей алгебры известно, что каждый многочлен с
действительными коэффициентами
![]()
может
быть представлен в виде произведения, содержащего сомножители вида ![]() и
и ![]() ,
причём квадратичный сомножители не имеют действительных корней. Если среди
сомножителей имеются совпадающие, то многочлен может быть представлен в
следующем виде
,
причём квадратичный сомножители не имеют действительных корней. Если среди
сомножителей имеются совпадающие, то многочлен может быть представлен в
следующем виде
![]() (2.1.5)
(2.1.5)
Числа
![]() – целые числа и называются
кратностями корней.
– целые числа и называются
кратностями корней.
Например,
![]() .
.
В
этом случае, число ![]() называется корнем многочлена
называется корнем многочлена ![]() кратности 3.
кратности 3.
После того как знаменатель дроби ![]() разложен на множители, приступают к
нахождению простейших дробей, составляющих в сумме данную дробь. Знаменателями
таких простейших дробей могут лишь линейные и квадратичные множители, входящие
в разложение
разложен на множители, приступают к
нахождению простейших дробей, составляющих в сумме данную дробь. Знаменателями
таких простейших дробей могут лишь линейные и квадратичные множители, входящие
в разложение ![]() , причём не в больших степенях, чем
они входят в это разложение. Поэтому каждому сомножителю
, причём не в больших степенях, чем
они входят в это разложение. Поэтому каждому сомножителю ![]() разложения
разложения ![]() в
разложении дроби
в
разложении дроби ![]() отвечает выражение вида
отвечает выражение вида
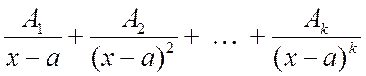 , (2.1.6)
, (2.1.6)
а
каждому сомножителю ![]() – выражение вида
– выражение вида
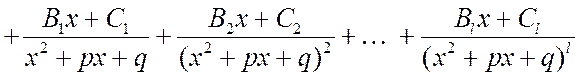 . (2.1.7)
. (2.1.7)
Отсюда получаем следующее практическое правило
разложения правильной рациональной дроби ![]() на
простейшие дроби.
на
простейшие дроби.
1. Разложить знаменатель ![]() на
линейные множители и квадратичные множители, не имеющие действительных корней.
на
линейные множители и квадратичные множители, не имеющие действительных корней.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.