Ты можешь стать умнее тремя путями: путем опыта – это самый горький путь; путем подражания – это самый легкий путь; путем размышления – это самый благородный путь.
Китайская пословица
Рассмотрим еще один класс функций, первообразные от которых можно записать в элементарных функциях, это интегралы вида
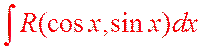
Рассмотрим еще один класс функций, первообразные от которых можно записать в элементарных функциях, это интегралы вида
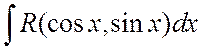 ,
,
где R(u,v) – рациональная функция двух переменных u и v. Такие интегралы, при помощи универсальной подстановки
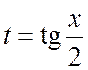 , (2.2.1)
, (2.2.1)
сводятся к интегрированию рациональных функций.
Действительно, используя формулы, выражающие синусы и косинусы через тангенс половинного угла:
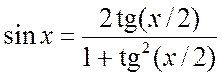 ,
, 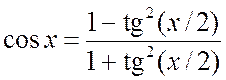 ,
, ![]() ,
,
находим
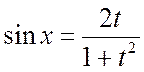 ,
, 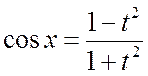 ,
,
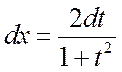 . (2.2.2)
. (2.2.2)
В результате, вместо интеграла от тригонометрического выражения мы получаем интеграл от рациональной функции:
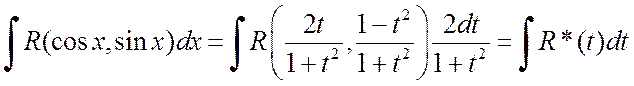 ,
,
где R*(t) – рациональная функция от t.
Таким образом, интегрирование любого тригонометрического рационального выражения при помощи универсальной подстановки сводится к интегрированию рациональных функций, которые, как известно, всегда интегрируются в элементарных функциях. Следовательно, первообразные тригонометрических рациональных выражений всегда можно выразить в элементарных функциях.
Пример 2.2.1. Вычислить интеграл
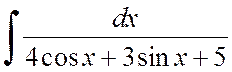 .
.
Решение. Применяя здесь универсальную подстановку, получим

 .
.
Метод интегрирования функций вида 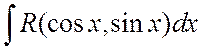 с помощью
универсальной подстановки всегда приводит к цели. Однако в силу своей общности
он не всегда является наилучшим, в смысле краткости и простоты преобразований.
Например, рассмотрим интеграл вида
с помощью
универсальной подстановки всегда приводит к цели. Однако в силу своей общности
он не всегда является наилучшим, в смысле краткости и простоты преобразований.
Например, рассмотрим интеграл вида
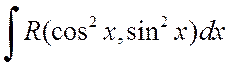 .
.
В этом случае удобнее сделать подстановку
![]() . (2.2.3)
. (2.2.3)
Тогда
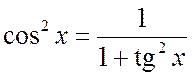 ,
, 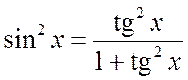 ,
,
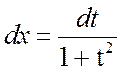 . (2.2.4)
. (2.2.4)
Пример 2.2.3. Вычислить интеграл
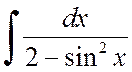 .
.
Решение.
Чтобы вычислить данный интеграл, воспользуемся подстановкой (2.2.3). Однако,
если вы не помните формул (2.2.4), то можно поступить следующим образом.
Разделим числитель и знаменатель на ![]() , в результате
получим
, в результате
получим
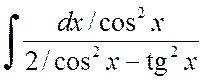 .
.
Так как
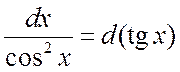 и
и 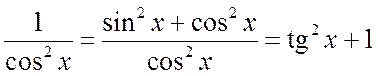 ,
,
то
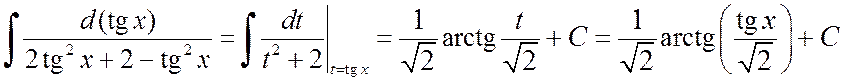 .
.
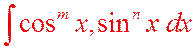
Интегралы данного вида также можно вычислить при помощи универсальной подстановки. Однако, как уже отмечалось, это не всегда рационально. Рассмотрим несколько случаев.
а) Пусть хотя бы одно из чисел: m или n– нечетное положительное число. Тогда, отделив от нечетной степени один сомножитель м внеся его под знак дифференциала, а оставшуюся часть преобразовав при помощи формулы
![]() , (2.2.5)
, (2.2.5)
получим в результате, что все подынтегральное выражение будет записано через синусы или косинусы.
Пример 2.2.4. Вычислить интегралы
а)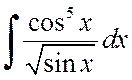 , б)
, б)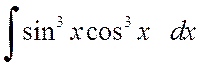 .
.
Решение. а) Преобразуем подынтегральное выражение в соответствие с приведенными рекомендациями:
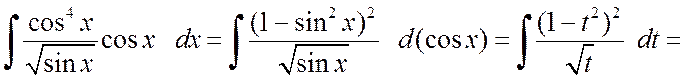
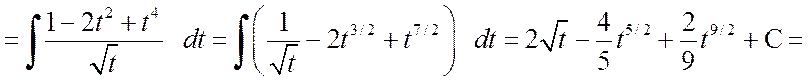
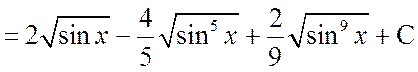 .
.
б) Поскольку обе степени нечетные, все равно какой множитель выносить под знак дифференциала – синус или косинус:
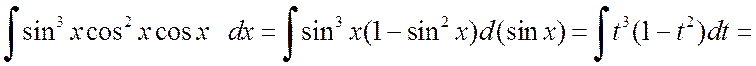
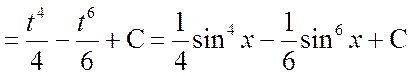 .
.
б) Пусть теперь m и n – четные неотрицательные числа. В этом случае следует применить тригонометрические формулы понижения степени:
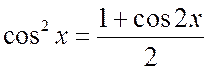 ,
, 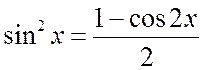 ,
,
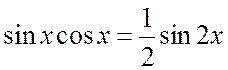 . (1.20)
. (1.20)
Пример 2.2.5. Вычислить интегралы
а)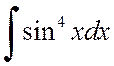 , б)
, б)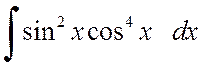 .
.
Решение.
а)
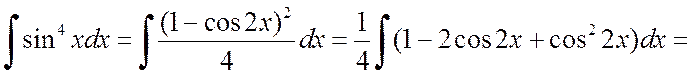
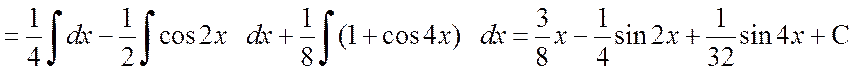 .
.
б) 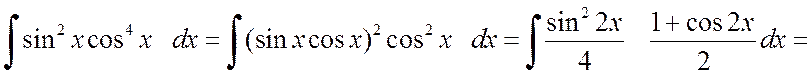
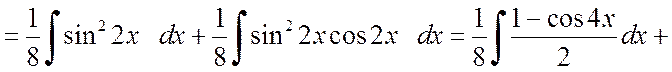
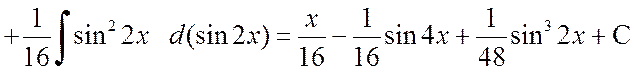 .
.
в) Пусть m+n – четное отрицательное число. В этом случае предыдущий прием не приводит к цели. Здесь подынтегральное выражение преобразуется по степенях tgx или ctgx при помощи формул:
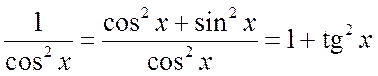 , (2.2.6)
, (2.2.6)
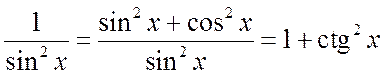 . (2.2.7)
. (2.2.7)
Пример 2.2.6. Вычислить интеграл
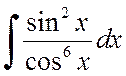 .
.
Решение.
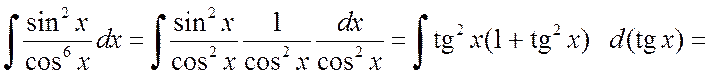
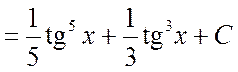 .
.
г) Пусть m+n=0, т.е. будем рассматривать интегралы вида:
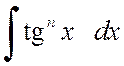 ,
, 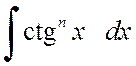 .
(2.2.8)
.
(2.2.8)
Для вычисления этих интегралов лучше всего воспользоваться формулами:
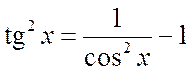 ,
, 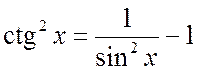 ,
(2.2.9)
,
(2.2.9)
Пример 2.2.7. Вычислить интегралы
а)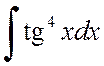 , б)
, б)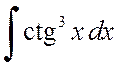 .
.
Решение.
а)
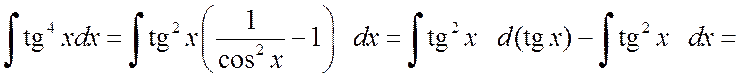
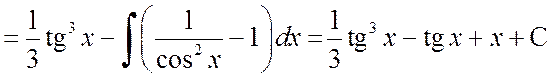 .
.
б)
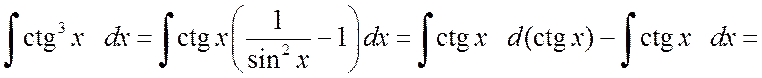
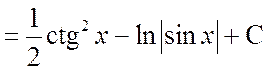 .
.
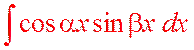
Для интегрирования произведения синусов и косинусов различных аргументов применяются тригонометрические формулы:
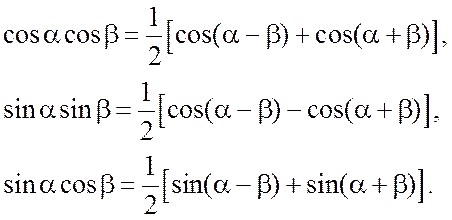 (2.2.9)
(2.2.9)
Пример 2.2.8. Вычислить интеграл
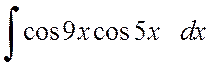 .
.
Решение. Применяя формулу произведения косинусов, получим
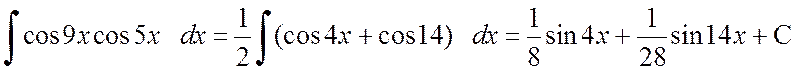 .
.
1. Почему интегралы от тригонометрических рациональных выражений всегда «берутся»?
2. Что такое универсальная подстановка. Почему она называется универсальной, на ваш взгляд?
3.
Как вычисляются интегралы вида ![]() ?
?
4.
Как вычисляются интегралы вида ![]() ? Можно ли здесь использовать универсальную
подстановку?
? Можно ли здесь использовать универсальную
подстановку?
5.
Как вычисляются интегралы вида ![]() ?
?
1. Вычислить интегралы, используя универсальную подстановку:
|
а) |
б) |
в) |
г) |
2. Вычислить интегралы, используя универсальную подстановку:
|
а) |
б) |
в) |
3.
Вычислить интегралы, используя подстановку ![]() :
:
|
а) |
б) |
в) |
4. Вычислить интегралы:
|
а) |
б) |
в) |
5. Вычислить интегралы:
|
а) |
б) |
в) |
6. Вычислить интегралы:
|
а) |
б) |
в) |
7. Вычислить интегралы:
|
а) |
б) |
в) |
8. Вычислить интегралы:
|
а) |
б) |
в) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.