«Только допустив бесконечно малую единицу для наблюдения – дифференциал истории, то есть однородные влечения людей и, достигнув искусства интегрировать (брать сумм этих бесконечно малых), мы можем надеяться на постигновение законов истории».
Л.Н. Толстой «Война и мир». Эпилог.
Интегральное исчисление – это раздел математики, появление которого связано с понятием определенного интеграла. Возникло интегральное исчисление из задач на определение площадей и объёмов. Для иллюстрации рассмотрим такую задачу.
Предположим, что нам нужно вычислить объем лимона. Он
имеет неправильную форму, и применить здесь какую-либо известную формулу объёма
нельзя. Можно найти объём с помощью взвешивания и использования формулы 
, но плотность лимона в различных
частях разная. Можно поступить следующим образом. Разрежем лимон на тонкие
дольки. Каждую дольку можно приближённо считать цилиндром с малой высотой.
Объём каждого такого цилиндра легко вычислить по известной формуле 
. Сложив объём маленьких цилиндров,
мы получим приближенное значение объёма всего цилиндра. Приближение будет тем
точнее, чем на более тонкие дольки мы будем разрезать лимон. Этот способ
вычисления объёмов предложил ещё в III в. до н.э. Архимед. Гениальный ум древнего грека
предвосхитил многие открытия XVII-XVIII вв.
Кстати, понятие неопределенного интеграла появилось гораздо позднее понятия определенного интеграл, в XVII в., когда Ньютоном и Лейбницем была установлена взаимосвязь между интегральным и дифференциальным исчислением.
Рассмотрим более простую задачу, чем вычисление объёма
лимона: вычисление площади криволинейной трапеции. Пусть задана непрерывная на
отрезке 
функция 
,
график которой лежит выше оси Ox. Кривая 
и прямые 
и 
,
а также ось Ox, ограничивают некоторую область плоскости, называемую
криволинейной трапецией (рис. 3.1).
Площадь криволинейной трапеции можно вычислить с
помощью тонких прямоугольников. Лейбниц считал, что криволинейная трапеция составлена
из бесконечно тонких прямоугольников (рис. 3.2). Каждый такой прямоугольник
поднимается над точкой x отрезка
и имеет высоту и ширину dx. Площадь
такого прямоугольника 
. Общая площадь S есть сумма
таких площадей и обозначается
.
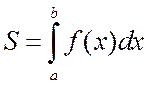Таким
образом, символ 
означает сумму и происходит
от удлинения буквы S (от лат. слова Summa).
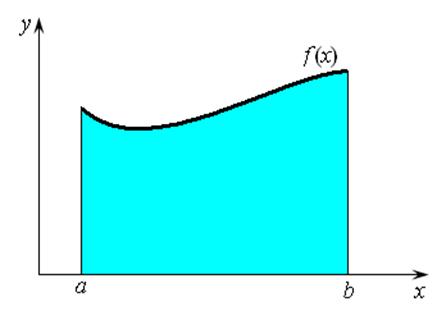
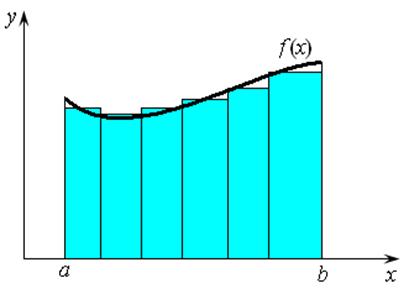
Рис. 3.1 Рис. 3.2
Понятно, что при вычислении площади нельзя обойтись конечным числом шагов. Интуитивно это чувствовали уже древнегреческие учёные. Правда они всячески пытались избежать бесконечных процессов. Ещё в V в. до н.э. древнегреческий философ Зенон Элейский привёл ряд возникающих при этом парадоксов, или апорий. Среди них наиболее известной является апория «Ахиллес и черепаха», которая гласит: Ахиллес, герой Троянской войны, не сможет догнать черепаху. В самом деле пока Ахиллес пробежит расстояние, отделяющее его от черепахи, она переберется на некоторое расстояние вперёд. Затем, когда Ахиллес преодолеет расстояние, вновь возникшее перед ним, черепаха снова переместится вперёд и т.д. Многие учёные пытались объяснить парадоксы Зенона. Но ни одно из предложенных объяснений нельзя считать до конца удовлетворительным. По-видимому, это сделать вообще невозможно, поскольку парадоксы отражают реально существующие противоречия между дискретным и непрерывным, конечным и бесконечным.
Великолепной попыткой вырваться из плена бесконечности при вычислении мер был метод исчерпывания, разработанный выдающимся древнегреческим мыслителем Евдоксом и плодотворно применявшийся многими его соотечественниками, в том числе Евклидом и Архимедом. Суть метода исчерпывания можно объяснить на следующем примере. При вычислении площади круга рассматривают вписанные и описанные правильные многоугольники с увеличивающимся числом сторон, вычисляют их площади и затем принимают за площадь круга предел площади этих многоугольников.
Понятно, что древние греки так делать не могли, они не знали теории пределов, тем более они любыми способами избегали бесконечных величин. Архимед, например, поступал следующим образом. Он проводил несколько последовательных вычислений, гениально угадывал каким-либо образом ответ, а затем уже строго (методом математической индукции) доказывал, что ответ он угадал правильно. В XVII в. число решенных подобным образом задач возросло неимоверно, однако единого алгоритма так создано и не было. Для каждой задачи требовался индивидуальный подход. И только в 70-х годах XVII в. И. Ньютоном и Г. Лейбницем независимо друг от друга был найдем этот алгоритм и было создано интегральное исчисление.
Несколько слов хочется сказать о великом немецком учёном Готфриде Лейбнице. С юных лет ему хотелось познать природу мира, и математика должна была стать решающим средством этого познания. Он был философом и лингвистом, историком и биологом, дипломатом и политическим деятелем, математиком и изобретателем. В частности, он создает дифференциальное и интегральное исчисления. Однако судьба сыграла с этим человеком злую шутку. Несмотря на огромное миролюбие Лейбница и его постоянное стремление к согласовыванию спорных взглядов, в последние годы жизни он был вовлечен в спор с Ньютоном о первенстве в деле создания дифференциального и интегрального исчислений. Этот спор был чрезвычайно раздут сторонниками обоих ученых. А правда была в том, что первые результаты получил Ньютон, а Лейбниц пришел к открытию собственным путем. Кроме того, результаты Лейбница стали известны ученым раньше и раньше опубликованы. Упомянутый спор отравил остаток жизни Лейбница и когда он умер, за его гробом шел только один человек – его друг.
По-видимому, этот спор имел в виду замечательный русский поэт В. Брюсов, когда написал такие строки:
О Лейбниц, о мудрец, создатель вещих книг!
Ты выше мира был, как древние пророки.
Твой век, дивясь тебе, пророчеств не достиг
И с лестью смешивал безумные упрёки.
Пусть функция f(x)
определена на отрезке 
. Этот отрезок разделим на n
произвольных, необязательно равных, частей:
a=x0 < x1 < ... < xn=b.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
