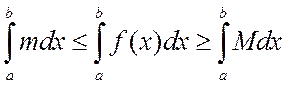 .
.
Заметим, что в силу геометрического смысла определенного интеграла
 .
(3.4)
.
(3.4)
С учетом этого получаем исходную оценку определенного интеграла.
Свойство 8. (Теорема о среднем значении). Если функции f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка с, что справедливо следующее равенство:
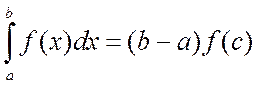 .
.
Отметим, что геометрически теорема о среднем означает, что площадь криволинейной трапеции равна площади прямоугольника со сторонами f(с) и (b–a). Поэтому эта теорема имеет огромное теоретическое значение в обосновании численных методов интегрирования, поскольку, по-существу, основная цель этих методов состоит в том, чтобы как можно точнее выбрать точку с.
Приближенные методы вычисления определенных интегралов основан на том, что определенный интеграл можно рассматривать как площадь криволинейной трапеции. Площадь такой трапеции можно вычислить, если заменить ее более простой фигурой: суммой прямоугольников, трапецией или других фигурой. Практическая значимость таких методов заключается в том, что точно вычислить определённый интеграл не всегда удаётся. К тому же подынтегральная функция часто даётся в табличном или даже графическом виде. В этих случаях можно использовать только приближённые методы. Мы познакомимся с двумя из них – методом прямоугольников и методом трапеций.
Разделим отрезок интегрирования [a,b] на n равных частей точками:
![]() ,
,
где h=(b–a)/n – шаг интегрирования. Заменим данную криволинейную трапецию ступенчатой фигурой, состоящей их n прямоугольников (см. рис. 3.2). Значение площади этой фигуры и будет давать приближенное значение искомого интеграла:
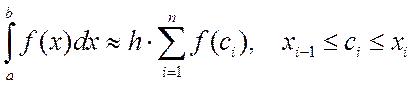 . (3.5)
. (3.5)
Полученное выражение называется формулой прямоугольников.
В качестве сi можно выбирать как левые (сi=xi–1), так и правые (сi=xi) границы участков разбиения. В этом случае площадь криволинейной трапеции будет приближенно равна сумме площадей либо левых, либо правых прямоугольников. Методы левых и правых прямоугольников дают приближенное значение определенного интеграла с точностью, пропорциональной шагу интегрирования h. Причем один из методов дает значение интеграла с избытком, а другой с недостатком. Поэтому в качестве более точного значения интеграла можно взять среднее арифметическое обоих методов, а разность между ним даст погрешность вычисления. Такой способ мы рассмотрели в примере 3.1.
Обычно под методом прямоугольников понимается случай, когда в качестве точек сi берутся середины участков разбиения, т.е. сi=(xi-1+xi)/2. В этом случае погрешность вычисления определенного интеграла будет пропорциональна h2, т.е. на порядок выше, чем у методов левых или правых прямоугольников.
Пример 3.2. Найти по формуле прямоугольников приближенное значение интеграла
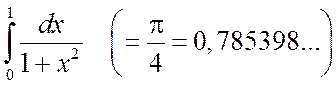 .
.
Решение. Разобьем
отрезок [0; 1] на 10 равных частей. Найдём на каждом отрезке середину ci и значение
функции 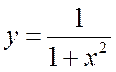 в этих точках. Составим таблицу
в этих точках. Составим таблицу
|
ci |
0,05 |
0,15 |
0,25 |
0,35 |
0,45 |
0,55 |
0,65 |
0,75 |
0,85 |
0,95 |
|
yi=f(ci) |
0,9995 |
0,9780 |
0,9442 |
0,8909 |
0,8316 |
0,7678 |
0,7029 |
0,6500 |
0,5806 |
0,5256 |
Откуда
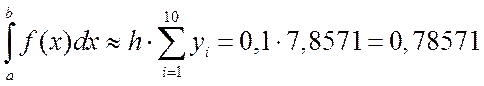 .
.
Погрешность
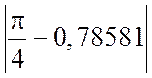 составляет
примерно 0,0004.
составляет
примерно 0,0004.
Вторым наиболее простым способом приближенного вычисления определенных интегралов является метод трапеций, который заключается в том, что вертикальные полосы заменяются не прямоугольниками, а трапециями. Другими словами, график функции f(x) заменяется ломаной линией (см. рис. 3.5).
|
|
Рис. 3.5 |
В результате, площадь всей фигуры будет складываться из площадей прямолинейных трапеций. Площадь каждой такой трапеции равна произведению полусуммы оснований на высоту:
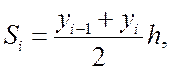
где yi=f(xi). Тогда квадратурная формула трапеций будет иметь вид
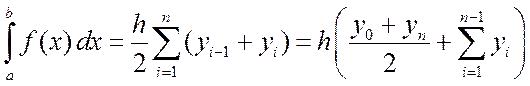 . (3.6)
. (3.6)
Отметим, что погрешность численного интегрирования определяется шагом интегрирования, для метода трапеций погрешность также пропорциональна h2. Уменьшая шаг интегрирования можно добиться большой точности вычислений.
Пример 3.3. Найти по формуле трапеций приближенное значение интеграла
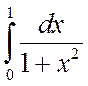 .
.
Решение. Разобьем
отрезок [0; 1] на 10 равных частей. В каждой точке найдем значение функции 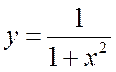 . Составим таблицу
. Составим таблицу
|
ci |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
yi=f(ci) |
1 |
0,9901 |
0,9615 |
0,9174 |
0,8621 |
0,8 |
0,7353 |
0,6711 |
0,6098 |
0,5525 |
0,5 |
Откуда
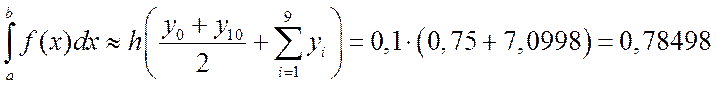 .
.
Погрешность
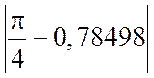 составляет
также примерно 0,0004.
составляет
также примерно 0,0004.
1. Как составляются интегральные суммы?
2. Зависит ли интегральная сумма от способа разбиения отрезка? от способа выбора промежуточных точек?
3. Что такое определённый интеграл? В чём он принципиально отличается от неопределённого?
4. Зависит ли определённый интеграл от способа разбиения отрезка? от способа выбора промежуточных точек?
5. Приведите и докажите линейное свойство определённых интегралов?
6. Сформулируйте свойства определённого интеграла, не характерные для неопределенных интегралов?
7. Опишите метод прямоугольников численного вычисления определённых интегралов?
8. Опишите метод трапеций численного вычисления определённых интегралов?
1. Пусть зависимость объема продаж данного товара от времени задана функцией
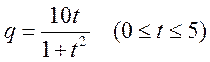 .
.
Тогда общий объем продаж Q равен площади заштрихованной фигуры (рис.3.6), т.е. опять площади криволинейной трапеции, и мы можем применить тот же метод исчерпывания для приближенного нахождения Q. Вычислить методом исчерпывания площадь криволинейной трапеции Q.
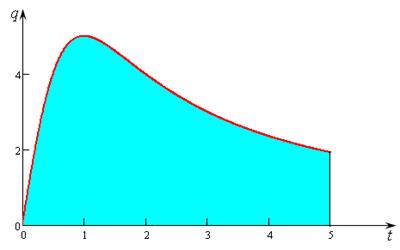
Рис. 3.6
2. Вычислить по формулам прямоугольников и трапеций для n=10 интегралы:
а) 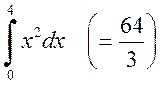 ; б)
; б) 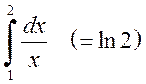 .
.
3. Найти
максимальное значение интегральной суммы функции ![]() на
отрезке
на
отрезке
[0; 1], если число отрезков разбиения равно 4.
4. Не вычисляя интегралов, выяснить, какой из интегралов больше:
|
а) |
б) |
5. Оценить интегралы:
|
а) |
б) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.