Изучение метода поочередного варьирования переменных

Санкт-Петербургский государственный технологический институт

(Технический университет)

Кафедра систем автоматизированного проектирования и управления                                                                                                                   Факультет.. 4.

      Курс….. 3

          Группа… 9082б

Учебная дисциплина:          Методы оптимитизации

Сравнение методов нелинейного программирования

Студенты                                                                                Жуков А.В.

                                                                              Чернухина П.А.

                                                                                                Далиденок Л.В.

                                                                                                Великий М.А.

                                                                                                           Берхман Д.М.

Руководитель                                                                         Песков И.А.               

Санкт-Петербург

2013г.

Лабораторная работа №3

«Изучение метода поочередного варьирования переменных»

Цель работы:

1. Ознакомление с одним из методов нелинейного программирования –методом поочередного варьирования  переменных;

2. Изучение алгоритма реализации указанного метода на ПЭВМ на примере решения задачи поиска экстремума функции двух переменных;

3. Исследование влияния параметров метода на  результаты поиска  экстремума.

Исходные данные:

1.Функция №2 F=(y1²+y2-11)²+(y1+y2²-7)²

2.Тип экстремума- минимум;

3.Критерии прекращения поиска экстремума функции:

Критерий 1	КР1	Точность вычисления функции
Критерий 2	КР2	Точность координат экстремума
Критерий 3	КР3	Количество циклов
Критерий 4	КР4	Количество вычислений целевой функции

Выполнение:

1.Построить функцию

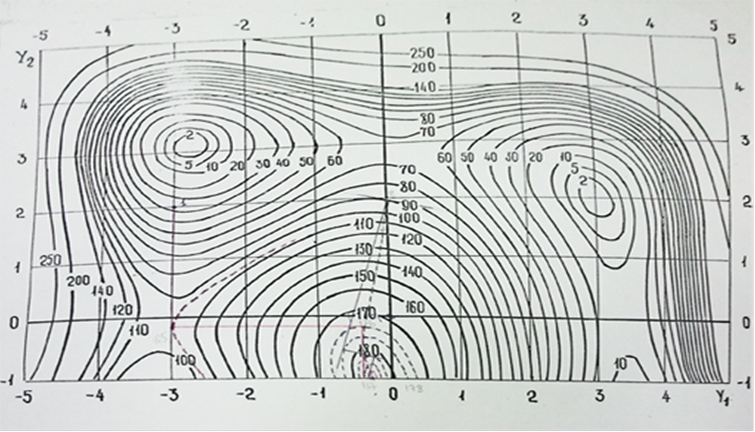
2.Определить при каких  минимально возможных значениях критерия КР3 может быть определен локальный экстремум.

Исходные значения:

КР3=5

Координаты исходной точки: (0;0)

Величины пробных шагов: Ш1=0,1, Ш2=0,1

Метод одномерного поиска(МОП)-метод половинного деления.

Критерий окончания поиска экстремума функции –КР3

Таблица№1

КР3	Y1	Y2	F(Y1;Y2)
0	0	0	170
1	3.39609	-1.80391	1.73643
2	3.58125	-1.84688	0,00052
3	3.58359	-1.84766	0,00004
4	3.58437	-1.84844	0,00000
5	3.58516	-1.84766	0,00003

Проведя расчеты видно что локальный экстремум возможен при минимальных значениях КР3 =4.

3.Исследовать влияния МОП на эффективность поиска экстремума функции для найденного значения КР3.

Таблица№2

МОП(0;0)	Y1	Y2	F	N	NumFunc
Метод половинного деления	3.58437	-1.84844	0,00000	4	269
Метод золотого сечения	3,58409	-1,84721	0,00002	4	213
Метод локализации экстремума	3,58433	-1,84819	0,00000	4	631
Метод с использованием  чисел Фибоначи	3,58455	-1,84807	0,00000	4	317

Сравнивая результаты методов поиска по заданным параметрам, можно судить, что метод половинного деления является оптимальным по совокупности затрат количества времени и точность нахождения экстремума.

4.Исследовать поверхность экстремумов стартуя их трех  различных точек

Y10;Y20	Y1	Y2	F	N	NumFunc
(0;0)	3.58516	-1.84766	0,00003	5	309
(-5;-5)	-3.77891	-3.28359	0,00002	5	259
(-5;5)	-2.80547	-3.13203	0,00002	5	283

6.Сравнить эффективность определения экстремума функции при использовании разных критериев прекращения поиска.

Исходные значения критериев:КР1=0,1;КР2=0,1;КР4=50.

Таблица№3

Критерий 1=0,1	F(Y1,Y2)	Y1	Y2	N	NumFunc
	170	0.0	0.0	0	0
	1,73643	3,39609	-1,80391	1	145
	0,00052	3,58125	-1,84688	2	189

Таблица№4

Критерий 2=0,1	F(Y1,Y2)	Y1	Y2	N	NumFunc
	170	0.0	0.0	0	0
	4,23591	3,35000	1,75000	1	121
	0,09401	3,05000	2,00000	2	145
	0,09401	2,95000	2,00000	3	159

Таблица№5

Критерий 4=50	F(Y1,Y2)	Y1	Y2	N	NumFunc
	170	0.0	0.0	0	0
	55,75220	2,30000	-0,10000	1	57

Заданные критерии прекращения поиска экстремума функции по сравнению с данным КР3, значительно экономят время вычисления, что к сожалению значительно влияет на точность вычисления.