





Результат учения равен произведению способности на старательность. Если старательность равна нулю, то и все произведение равно нулю, а способности есть у каждого.
Понятие определенного интеграла находит широкое применение на практике. В частности, при помощи определенных интегралов можно вычислять площади фигур, длины кривых, объемы тел и т.д. В связи с этим возникает вопрос: в каких случаях можно использовать понятие определенного интеграла? Оказывается, что определенный интеграл можно использовать только в тех случаях, если вычисляемая величина обладает свойством аддитивности. Это означает, что изучаемую величину можно представить в виде суммы её частей. Так площадь фигуры равна сумме площадей её частей, длина кривой равна сумме её частей и т.п. Следовательно, для таких величин можно составить интегральные суммы и при помощи предельного перехода переходить к определенным интегралам.
Пусть функция ![]() неотрицательна
и непрерывна на отрезке
неотрицательна
и непрерывна на отрезке ![]() . Тогда по
геометрическому смыслу определенного интеграла площадь под кривой
. Тогда по
геометрическому смыслу определенного интеграла площадь под кривой ![]() на
на ![]() числена
равна определенному интегралу
числена
равна определенному интегралу
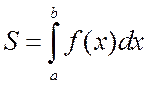 .
.
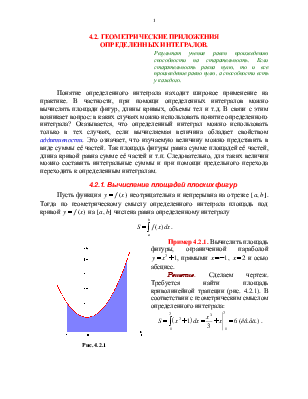
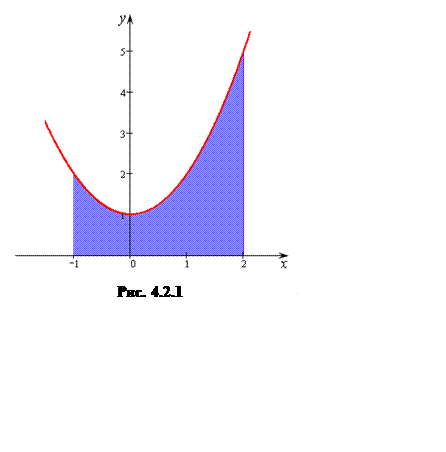 Пример 4.2.1. Вычислить площадь фигуры, ограниченной параболой
Пример 4.2.1. Вычислить площадь фигуры, ограниченной параболой ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью абсцисс.
и осью абсцисс.
Решение. Сделаем чертеж. Требуется найти площадь криволинейной трапеции (рис. 4.2.1). В соответствии с геометрическим смыслом определенного интеграла:
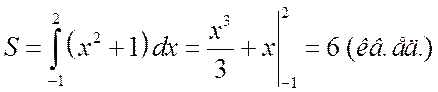 .
.
Пусть функция ![]() неположительна
и непрерывна на отрезке
неположительна
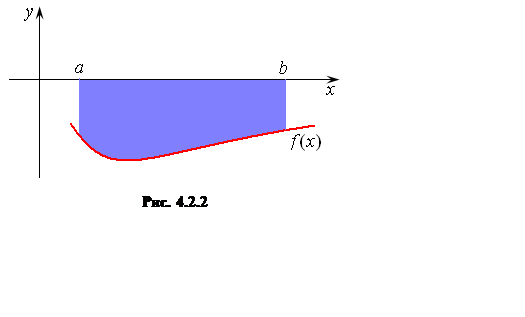
и непрерывна на отрезке ![]() (рис. 4.2.2).
Тогда площадь над кривой
(рис. 4.2.2).
Тогда площадь над кривой ![]() на
на ![]() числена равна определенному интегралу
взятому со знаком «минус»:
числена равна определенному интегралу
взятому со знаком «минус»:
 |
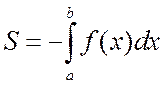 .
(4.2.1)
.
(4.2.1)
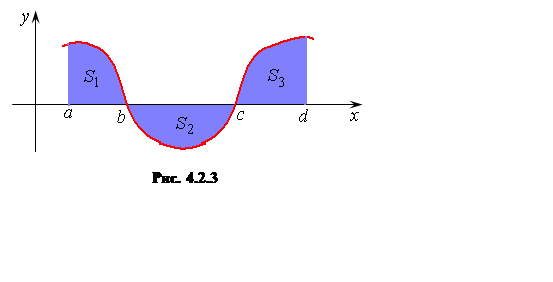 |
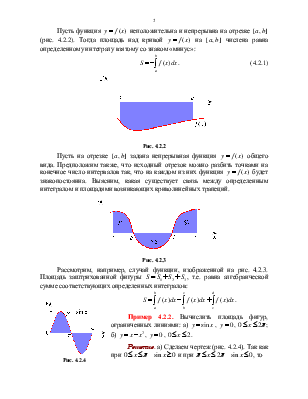
Рассмотрим, например, случай функции, изображенной на
рис. 4.2.3. Площадь заштрихованной фигуры ![]() ,
т.е. равна алгебраической сумме соответствующих определенных интегралов:
,
т.е. равна алгебраической сумме соответствующих определенных интегралов:
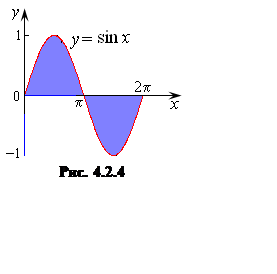
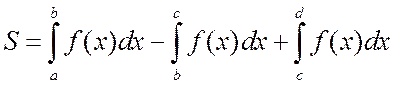 .
.
Пример 4.2.2. Вычислить площадь фигур, ограниченных линиями: а) ![]() ,
, ![]() ,
, ![]() ; б)
; б) ![]() ,
,
![]() ,
, ![]() .
.
Решение. а)
Сделаем чертеж (рис. 4.2.4). Так как при ![]()
![]() и при
и при ![]()
![]() , то
, то
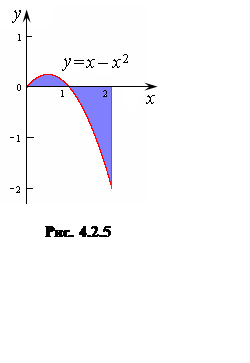
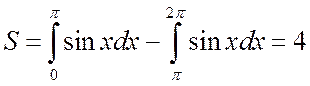 (кв. ед.)
(кв. ед.)
Отметим, что если бы мы не учитывали знаки подынтегральной функции, то получили бы
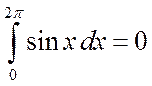 .
.
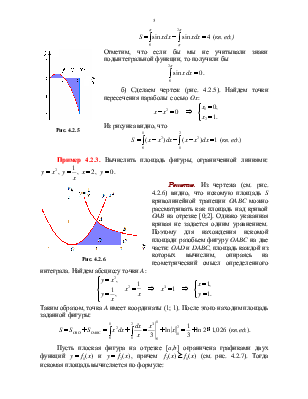
б) Сделаем чертеж (рис. 4.2.5). Найдем точки пересечения параболы с осью Ox:
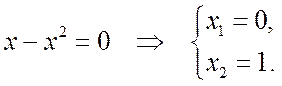
Из рисунка видно, что
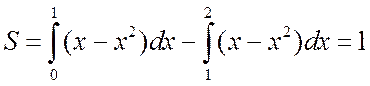 (кв. ед.)
(кв. ед.)
Пример 4.2.3. Вычислить площадь фигуры, ограниченной линиями: ![]() ,
, 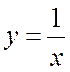 ,
,
![]() ,
, ![]() .
.
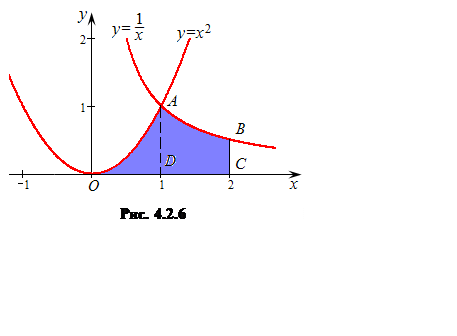 Решение. Из чертежа (см. рис. 4.2.6) видно, что искомую
площадь S криволинейной
трапеции OABC можно рассматривать как площадь над кривой OAB
на отрезке [0;2]. Однако указанная кривая не задается одним уравнением. Поэтому
для нахождения искомой площади разобьем фигуру OABC на две
части: OAD и DABC, площадь каждой из которых вычислим, опираясь на
геометрический смысл определенного интеграла. Найдем абсциссу точки A:
Решение. Из чертежа (см. рис. 4.2.6) видно, что искомую
площадь S криволинейной
трапеции OABC можно рассматривать как площадь над кривой OAB
на отрезке [0;2]. Однако указанная кривая не задается одним уравнением. Поэтому
для нахождения искомой площади разобьем фигуру OABC на две
части: OAD и DABC, площадь каждой из которых вычислим, опираясь на
геометрический смысл определенного интеграла. Найдем абсциссу точки A:
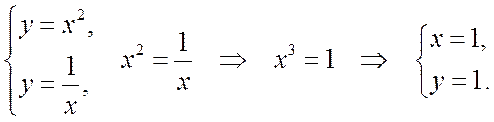
Таким образом, точка A имеет координаты (1; 1). После этого находим площадь заданной фигуры:
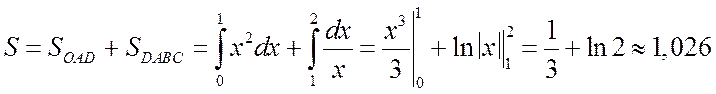 (кв.ед.).
(кв.ед.).
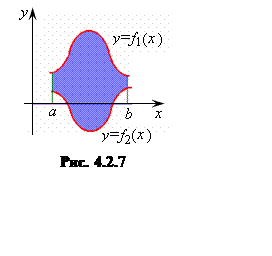
Пусть плоская фигура на отрезке [a,b]
ограничена графиками двух функций ![]() и
и ![]() , причем
, причем ![]() (см. рис. 4.2.7). Тогда искомая площадь вычисляется
по формуле:
(см. рис. 4.2.7). Тогда искомая площадь вычисляется
по формуле:
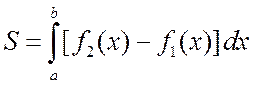 . (4.2.2)
. (4.2.2)
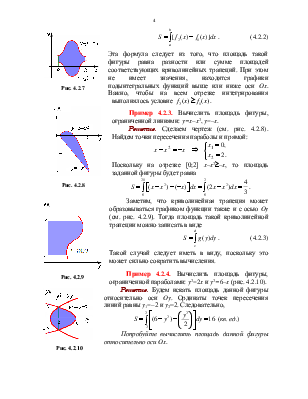
 Эта
формула следует из того, что площадь такой фигуры равна разности или сумме
площадей соответствующих криволинейных трапеций. При этом не имеет значения,
находятся графики подынтегральных функций выше или ниже оси Ox.
Важно, чтобы на всем отрезке интегрирования выполнялось условие
Эта
формула следует из того, что площадь такой фигуры равна разности или сумме
площадей соответствующих криволинейных трапеций. При этом не имеет значения,
находятся графики подынтегральных функций выше или ниже оси Ox.
Важно, чтобы на всем отрезке интегрирования выполнялось условие ![]() .
.
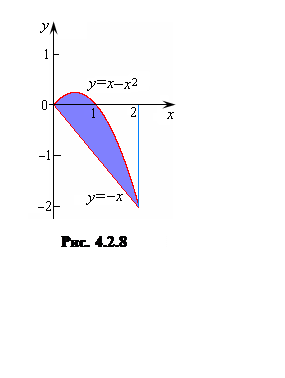
Пример 4.2.3. Вычислить площадь фигуры, ограниченной линиями: y=x–x2, y=–x.
Решение. Сделаем чертеж (см. рис. 4.2.8). Найдем точки пересечения параболы и прямой:
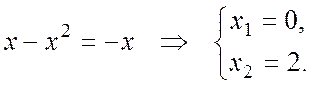
Поскольку на отрезке [0;2] x–x2³–x, то площадь заданной фигуры будет равна
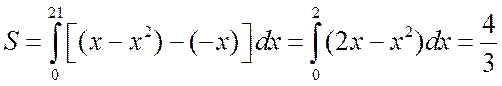 .
.
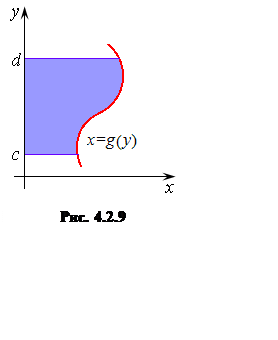 Заметим, что криволинейная трапеция может образовываться
графиком функции также и с осью Oy (см. рис. 4.2.9). Тогда
площадь такой криволинейной трапеции можно записать в виде
Заметим, что криволинейная трапеция может образовываться
графиком функции также и с осью Oy (см. рис. 4.2.9). Тогда
площадь такой криволинейной трапеции можно записать в виде
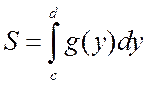 . (4.2.3)
. (4.2.3)
Такой случай следует иметь в виду, поскольку это может сильно сократить вычисления.
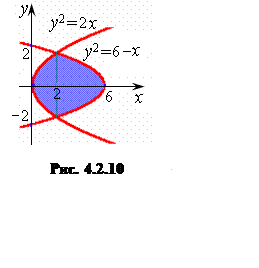 Пример 4.2.4.
Вычислить площадь фигуры, ограниченной параболами: y2=2x и y2=6–x(рис.
4.2.10).
Пример 4.2.4.
Вычислить площадь фигуры, ограниченной параболами: y2=2x и y2=6–x(рис.
4.2.10).
Решение. Будем искать площадь данной фигуры относительно оси Oy. Ординаты точек пересечения линий равны y1=–2 и y2=2. Следовательно,
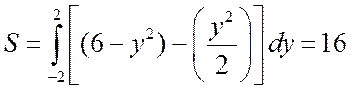 (кв. ед.)
(кв. ед.)
Попробуйте вычислить площадь данной фигуры относительно оси Ox.
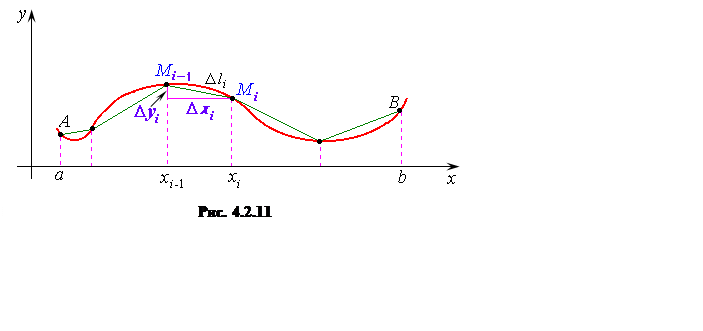 |
Длину ![]() малой дуги
малой дуги ![]() линии
линии ![]() заменяем
длиной отрезка
заменяем
длиной отрезка ![]() , соединяющего точки
, соединяющего точки ![]() и
и ![]() .
По теореме Пифагора
.
По теореме Пифагора
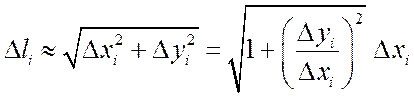 .
.
Тогда длина дуги кривой AB будет приближенно равна
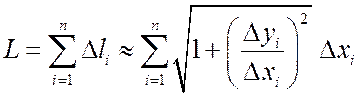 .
.
Если
существует предел ломанных, вписанных в кривую, при ![]() ,
то этот предел будет равен длине дуги кривой AB:
,
то этот предел будет равен длине дуги кривой AB:
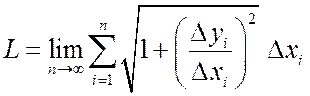 .
.
Заметим, что при ![]() отношение
в этом выражении превращается в производную, т.е.
отношение
в этом выражении превращается в производную, т.е.
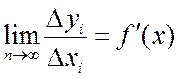 .
.
В результате, по определению определенного интеграла
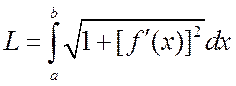 (4.2.4)
(4.2.4)
Пример 4.2.5. Вычислить длину: а) полукубической параболы ![]() , если
, если
![]() ; б) линии
; б) линии ![]() ,
если
,
если ![]() .
.
Решение.а) Поскольку y=x3/2, 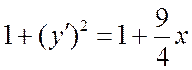 , то
, то
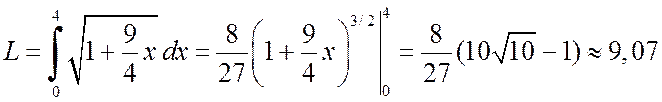 (ед.).
(ед.).
б) Поскольку 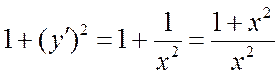 , то
, то
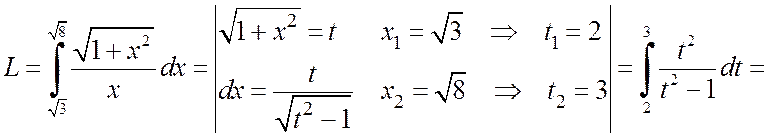
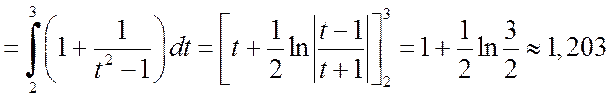 (ед.).
(ед.).
 |
При решении задачи применим тот же подход, который был
использован при нахождении площади криволинейной трапеции. Разобьем отрезок ![]() произвольным образом на n частей и на
каждом участке произвольно выберем точку xi.
При вращении кривой
произвольным образом на n частей и на
каждом участке произвольно выберем точку xi.
При вращении кривой ![]() вокруг оси Ox каждый
прямоугольник высотой
вокруг оси Ox каждый
прямоугольник высотой ![]() и основанием
и основанием ![]() описывает цилиндр с радиусом
описывает цилиндр с радиусом ![]() и высотой
и высотой ![]() .
Сумма объемов всех цилиндров приближенно равна объему тела вращения и легко
подсчитывается:
.
Сумма объемов всех цилиндров приближенно равна объему тела вращения и легко
подсчитывается:
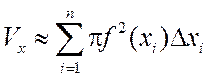 .
.
Нетрудно заметить, что это выражение является
интегральной суммой непрерывной на ![]() функции
функции ![]() , при
, при ![]() (
(![]() ) ее предел существует и равен
определенному интегралу. С другой стороны, при
) ее предел существует и равен
определенному интегралу. С другой стороны, при ![]() объем
ступенчатого тела вращения стремится к объему тела вращения:
объем
ступенчатого тела вращения стремится к объему тела вращения:
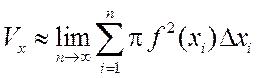 .
.
В результате, получаем формулу
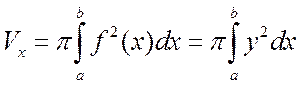 (4.2.5)
(4.2.5)
Пример 4.2.6. Вычислить объем тела, образованного вращением вокруг
оси Ox эллипса 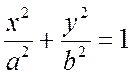 .
.
 Решение. Из уравнения эллипса имеем
Решение. Из уравнения эллипса имеем
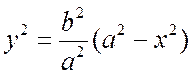 .
.
Тогда из формулы (4.2.5) находим объем эллипсоида вращения (рис. 4.2.13):
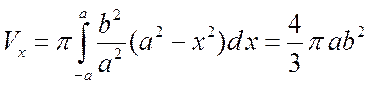 (куб. ед.).
(куб. ед.).
Формально, заменяя в формуле (4.2.5) переменную x на y,
получаем формулу для вычисления объема ![]() тела,
полученного от вращения криволинейной трапеции вокруг оси Oy:
тела,
полученного от вращения криволинейной трапеции вокруг оси Oy:
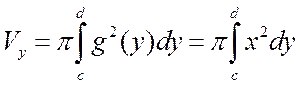 (4.2.6)
(4.2.6)
 Пример 4.2.7. Вычислить объем тела, образованного вращением вокруг
оси Oy фигуры, ограниченной параболой и осью ординат.
Пример 4.2.7. Вычислить объем тела, образованного вращением вокруг
оси Oy фигуры, ограниченной параболой и осью ординат.
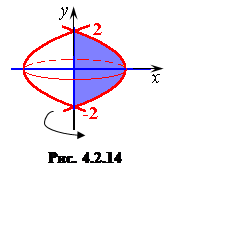
Решение. В соответствии с рис. 4.2.14 объем получающейся фигуры вращения будет равен:
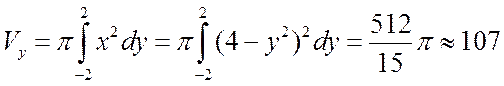 (куб. ед.).
(куб. ед.).
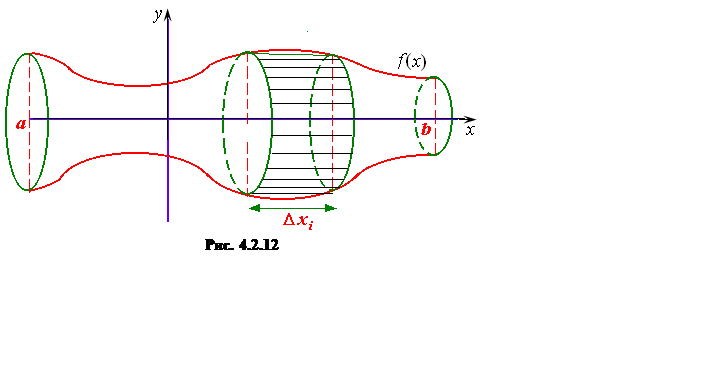
Рассмотрим теперь поверхность, которая образуется при
вращении вокруг оси Ox кривой,
образуемой графиком непрерывной на отрезке ![]() функции
функции
![]() (рис. 4.2.12). Требуется найти
площадь этой поверхности вращения.
(рис. 4.2.12). Требуется найти
площадь этой поверхности вращения.
Впишем в график функции ![]() ломаную
линию, соответствующую разбиению a=x0<x1< ... <xn=b. Каждое звено ломаной линии при вращении вокруг оси Ox
описывает боковую поверхность усеченного конуса, площадь которого равна
ломаную
линию, соответствующую разбиению a=x0<x1< ... <xn=b. Каждое звено ломаной линии при вращении вокруг оси Ox
описывает боковую поверхность усеченного конуса, площадь которого равна
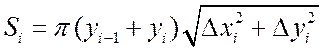 .
.
Тогда площадь всей поверхности вращения приближенно будет равна
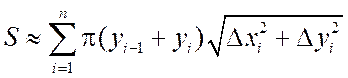 .
.
Ранее мы рассмотрели, что длина одного звена ломаной равна
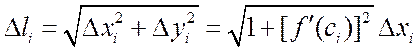 .
.
Тогда получится следующая сумма
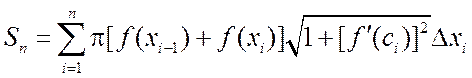 ,
,
которая
в пределе ![]() дает точное значение площади
вращения. Можно показать, что предел этой суммы равен пределу интегральной
суммы для функции, т.е.
дает точное значение площади
вращения. Можно показать, что предел этой суммы равен пределу интегральной
суммы для функции, т.е.
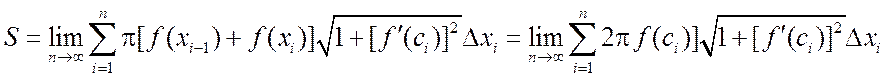 .
.
В результате, получаем формулу
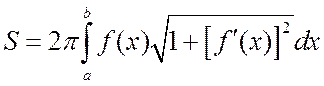 (4.2.7)
(4.2.7)
Пример 4.2.8. Вычислить площадь поверхности, образованной вращением
вокруг оси Ox одной арки синусоиды ![]() .
.
Решение. Согласно формуле (4.2.7), получим
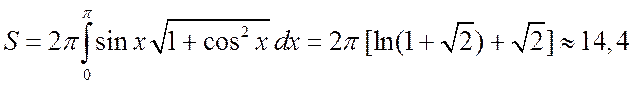 .
.
1. В чём состоит геометрический смысл определённого интеграла и как это используется для вычисления площадей плоских фигур?
2. Как вычисляется площадь фигуры, ограниченной осью абсцисс и графиком функции, если график несколько раз пересекает ось Ox?
3. Как вычислить площадь криволинейной трапеции, если график состоит из нескольких линий?
4. Как вычисляются площади фигур, ограниченных несколькими линиями?
5. Можно ли вычислить площадь фигуры, являющейся криволинейной трапецией относительно оси ординат?
6. Обоснуйте формулу вычисления длины дуги кривой.
7. Обоснуйте формулу вычисления объема тела вращения, относительно оси Ox? оси Oy?.
8. Обоснуйте формулу вычисления площади поверхности вращения относительно оси Ox?
1. Найти площади криволинейных трапеций, ограниченных:
а)
прямыми ![]() и осью абсцисс;
и осью абсцисс;
б)
кривой ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью абсцисс;
и осью абсцисс;
в)
кривой ![]() , прямой
, прямой ![]() и
осью абсцисс;
и
осью абсцисс;
г)
кривой ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью абсцисс;
и осью абсцисс;
д)
кривой ![]() и прямыми
и прямыми ![]() ,
,
![]() .
.
2. Вычислить площади фигур, ограниченных:
а)
параболой ![]() , осями координат и прямой
, осями координат и прямой ![]() ;
;
б)
гиперболой ![]() и прямыми
и прямыми ![]() ,
,
![]() ;
;
в)
параболой ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью абсцисс;
и осью абсцисс;
г)
кривой ![]() , прямыми
, прямыми ![]() ,
, ![]() и осью абсцисс;
и осью абсцисс;
д)
параболой ![]() , осями координат и прямой
, осями координат и прямой ![]() .
.
3. Вычислить площади фигур, ограниченных:
а)
линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
б)
линиями ![]() ,
, ![]() ,
, ![]() ;
;
в)
линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
4. Вычислить площади фигур, ограниченных линиями:
а)
![]() ,
, ![]() ;
;
б)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
;
в)
![]() ,
, ![]() ;
;
г)
![]() ,
, ![]() .
.
5. Вычислить площади фигур, ограниченных линиями:
а)
![]() ,
, ![]() ,
, ![]() и осью ординат;
и осью ординат;
б)
![]() ,
, ![]() ,
, ![]() .
.
6. Найти длины дуг следующих кривых:
а)
![]() от
от ![]() до
до
![]() ;
;
б)
![]() от
от ![]() до
до
![]() ;
;
в)
![]() от
от ![]() до
до
![]() .
.
7. Найти объемы тел, образовавшихся при вращении вокруг оси Ox криволинейных трапеций, ограниченных линиями:
а)
![]() ,
, ![]() при
при
![]() ;
;
б)
![]() ,
, ![]() при
при
![]() ;
;
в)
![]() ,
, ![]() при
при
![]() ;
;
г)
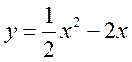 ,
, ![]() ;
;
д)
![]() ,
, ![]() при
при
![]() ;
;
е)
![]() ,
, ![]() при
при
![]() ;
;
ж)
![]() ,
, ![]() при
при
![]() .
.
8. Найти объемы тел, образовавшихся при вращении вокруг оси Oy криволинейных трапеций, ограниченных линиями:
а)
![]() ,
, ![]() ,
, ![]() ;
;
б)
![]() ,
, ![]() ,
, ![]() ;
;
в)
![]() ,
, ![]() ;
;
д)
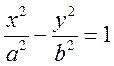 ,
, ![]() .
.
9. Найти площади поверхностей, полученных при вращении вокруг оси Ox следующих кривых:
а)
![]() ,
, ![]() при
при
![]() ;
;
б)
![]() при
при ![]() ;
;
в)
![]() при
при ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.