Математика \ Высшая математика

Аналитические методы вычисления определенных интегралов. Формула Ньютона-Лейбница

Страницы работы

6 страниц (Word-файл)

Скачать файл

Содержание работы

4. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.
ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА.

«Тот, кто имеет достаточные навыки в анализе, сможет всё увидеть с необычайной лёгкостью».

Л. Эйлер

Вычисление определённых интегралов при помощи интегральных сумм занятие довольно хлопотное. Поэтому нужен более простой и в то же время универсальный приём вычисления определённых интегралов без обращения к интегральным суммам. И такой способ был найден. Он основан на использовании понятия первообразной, т.е. производной. В первую очередь разработка такого метода связывают с именами И. Ньютона и Г. Лейбница.

4.1. Интеграл с переменным верхним пределом

Если функция интегрируема на отрезке , то она интегрируема и на любом меньшем отрезке. Следовательно, мы можем рассматривать определенный интеграл с переменным верхним пределом

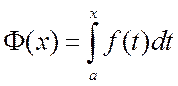. (4.1)

Поскольку при разных значениях x получаются различные значения интеграла, то мы можем говорить о некоторой функции F(x). Оказывается, что эта функция является первообразной для , т.е. справедлива следующая теорема, которую впервые рассмотрел И. Барроу, учитель И. Ньютона.

Теорема 4.1 (теорема Барроу). Если функция f(x) непрерывна на отрезке [a,b], то функция Ф(x) дифференцируема на этом отрезке, причем

Иными словами, интеграл с переменным верхним пределом является первообразной для непрерывной подынтегральной функции.

Доказательство. Зададим в произвольной точке xÎ[a,b] приращение Dx такое, чтобы x+DxÎ[a,b], тогда новое значение функции Ф(x), с учетом свойства 3, равно

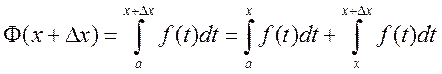Отсюда получим приращение функции

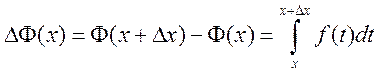Применив к полученному интегралу теорему о среднем, получим

где . Тогда

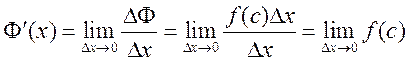Так как при , то

а вследствие непрерывности функции

Таким образом, . Теорема доказана.

Замечание. Из доказанной теоремы, в частности, следует, что любая непрерывная функция имеет первообразную, поскольку в этом случае существует функция (4.1), которая является первообразной для функции f(x). Таким образом, производная от интеграла по переменному верхнему пределу равна значению подынтегральной функции f(t) при t=x.

Пример 4.1. Вычислить производную

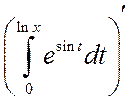Решение. В данном случае воспользуемся правилом дифференцирования сложной функции. Тогда получим

4.2. Формула Ньютона-Лейбница

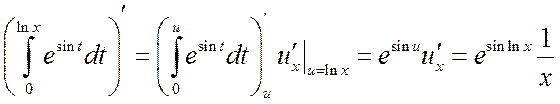Формула Барроу (4.1) позволяет уже естественным образом получить основную формулу математического анализа, связывающую в единое целое дифференциальное и интегральное исчисления.

Теорема 4.2. (формула Ньютона-Лейбница). Если функция f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо ее первообразная на этом отрезке, то имеет место следующая формула:

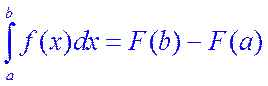. (4.2)

Доказательство. В соответствии с выше рассмотренной теоремой функция

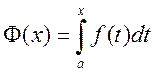будет первообразной для функции f(x). Поскольку все первообразные для одной и той же функции отличаются друг от друга на постоянную величину, то можно написать

Пусть x=a, тогда

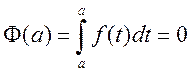и ,

отсюда C=–F(a) и тогда

или .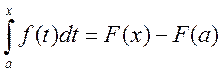

Пусть теперь x=b, тогда

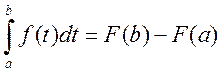или, заменив tна x, получим исходную формулу.

Формула Ньютона-Лейбница сводит вычисление определённого интеграла от функции f(x) к нахождению её первообразной F(x). Эта формула свидетельствует о глубокой связи между интегральным и дифференциальным исчислениями. Поэтому формулу (4.2) называют основной формулой математического анализа.

Первым шагом при вычислении определённого интеграла является нахождение первообразной, вторым – вычисление значения первообразной в точках b и a. Поэтому формулу Ньютона-Лейбница записывают в виде

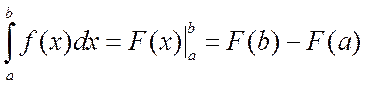. (4.3)

Символ называется знаком двойной подстановки.

Таким образом, формула Ньютона-Лейюница даёт аналитический способ вычисления определенных интегралов. Однако она имеет практическую ценность только в том случае, когда известна первообразная подынтегральной функции.

Пример 4.2. Вычислить интегралы

а) 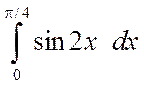, б) .

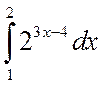Решение.

а) ,

б) .

4.3. Метод замены переменной в определенных интегралах

Также и для неопределённых интегралов основным методом вычисления определённых интегралов является метод замены переменной, но здесь, в отличие от неопределённых интегралов, имеются некоторые особенности.

Теорема 4.3. Если функция f(x) непрерывна на отрезке [a,b], а функция x=j(t) дифференцируема на отрезке [t₁,t₂], где t₁=a и t₂=b, то имеет место формула:

. (4.4)

Доказательство. Пусть F(x) – первообразная для функции f(x). Тогда в соответствии с формулой Ньютона-Лейбница для обоих интегралов можно записать

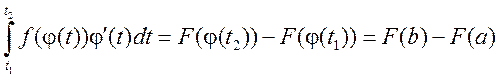
т.е. мы получили, что оба интеграла равны, что и требовалось доказать.

Отметим, что при вычислении определенных интегралов методом замены переменной нет необходимости возвращения к старой переменной, поскольку при вычислении преобразованного интеграла все равно получится число, равное исходному интегралу. Однако, обратите внимание, что при преобразовании интеграла при помощи метода замены переменной преобразуется не только подынтегральное выражение, но и пределы интегрирования.

Пример 4.3. Вычислить интегралы

а) 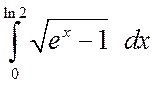, б) .

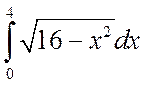Решение. а) Сделаем замену . Тогда и dx=2tdt/(1+t²). Поскольку при x=0 t=0 и при x=ln2 t=1, то получим

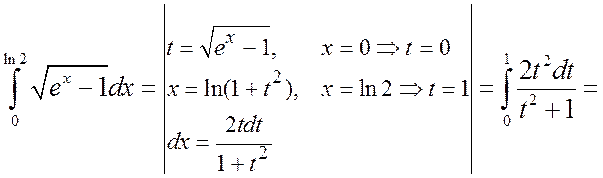
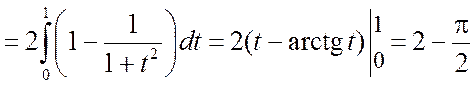б) Сделаем тригонометрическую подстановку x=4sint. Тогда

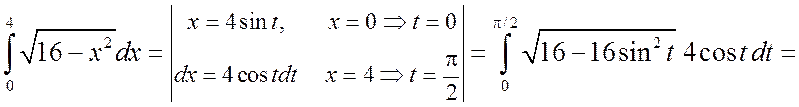
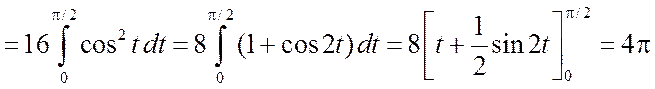Заметим, что при использовании метода замены переменной необходимо проверять выполнение всех перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен неверный результат.

Пример 4.4. Вычислить интеграл .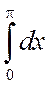

Решение. С одной стороны, имеем

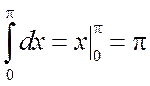С другой стороны,

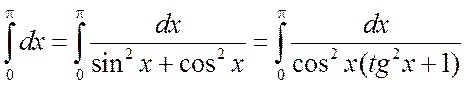Подстановка tgx=t формально приводит к следующему результату:

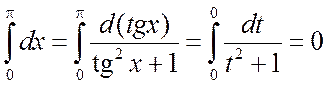Получен неверный результат. Это произошло потому, что функция t=tgx имеет разрыв при x=p/2 и не удовлетворяет условиям теоремы.

4.4. Метод интегрирования по частям
в определенных интегралах

Для определённых интегралов также справедлива и формула интегрирования по частям.

Теорема 4.3. Если функции u=u(x) и v=v(x) непрерывны вместе со своими производными на отрезке [a,b], то имеет место формула:

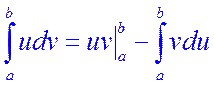Доказательство. Поскольку (uv)¢=u¢v+uv¢, то функция uv является первообразной для функции u¢v+uv¢. Тогда по формулу Ньютона-Лейбница получаем

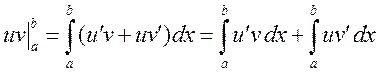что равносильно искомому равенству, поскольку по определению дифференциала u¢(x)dx=du и v¢(x)dx=dv.

Пример 4.4. Вычислить интегралы

а) 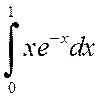, б) .

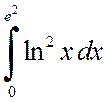Решение. а) Воспользуемся формулой интегрирования по частям, для этого положим u=x, dv=e^–^xdx, откуда du=dx, v=–e^–^x. Тогда

б) Применяя формулу интегрирования по частям, получим

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

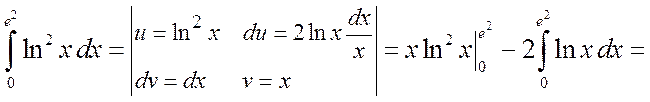
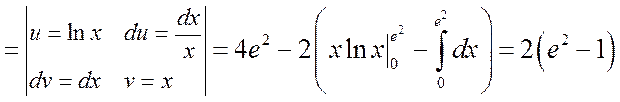1. Докажите формулу Барроу.

2. Докажите формулу Ньютона-Лейбница?

3. Какое значение имеет формула Ньютона-Лейбница для математического анализа?

4. Обоснуйте формулу замены переменных для определённых интегралов? В чём особенности использования этого метода по-сравнению с неопределенным интегралом?

5. Обоснуйте формулу интегрирования по частям для определённых интегралов? В чём особенности использования этого метода по-сравнению с неопределенным интегралом?